Machine Intelligence on Wireless Edge Networks

Deep neural network (DNN) inference on power-constrained edge devices is bottlenecked by costly weight storage and data movement. We introduce MIWEN, a radio-frequency (RF) analog architecture that ``disaggregates'' memory by streaming weights wirelessly and performing classification in the analog front end of standard transceivers. By encoding weights and activations onto RF carriers and using native mixers as computation units, MIWEN eliminates local weight memory and the overhead of analog-to-digital and digital-to-analog conversion. We derive the effective number of bits of radio-frequency analog computation under thermal noise, quantify the energy--precision trade-off, and demonstrate digital-comparable MNIST accuracy at orders-of-magnitude lower energy, unlocking real-time inference on low-power, memory-free edge devices.

Disaggregated Deep Learning via In-Physics Computing at Radio Frequency

Modern edge devices, such as cameras, drones, and Internet-of-Things nodes, rely on deep learning to enable a wide range of intelligent applications, including object recognition, environment perception, and autonomous navigation. However, deploying deep learning models directly on the often resource-constrained edge devices demands significant memory footprints and computational power for real-time inference using traditional digital computing architectures. In this paper, we present WISE, a novel computing architecture for wireless edge networks designed to overcome energy constraints in deep learning inference. WISE achieves this goal through two key innovations: disaggregated model access via wireless broadcasting and in-physics computation of general complex-valued matrix-vector multiplications directly at radio frequency. Using a software-defined radio platform with wirelessly broadcast model weights over the air, we demonstrate that WISE achieves 95.7% image classification accuracy with ultra-low operation power of 6.0 fJ/MAC per client, corresponding to a computation efficiency of 165.8 TOPS/W. This approach enables energy-efficient deep learning inference on wirelessly connected edge devices, achieving more than two orders of magnitude improvement in efficiency compared to traditional digital computing.

Micro-Ring Perceptron Sensor for High-Speed, Low-Power Radio-Frequency Signal

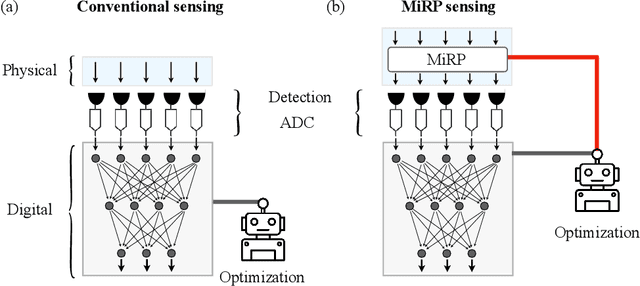
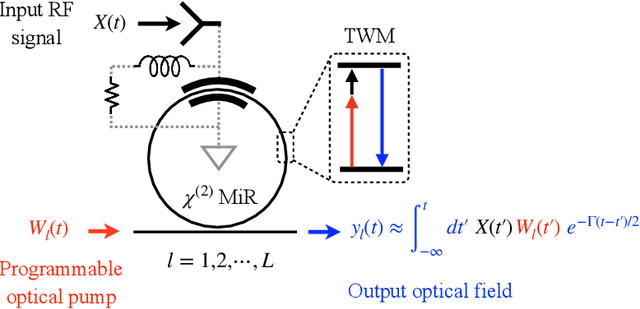
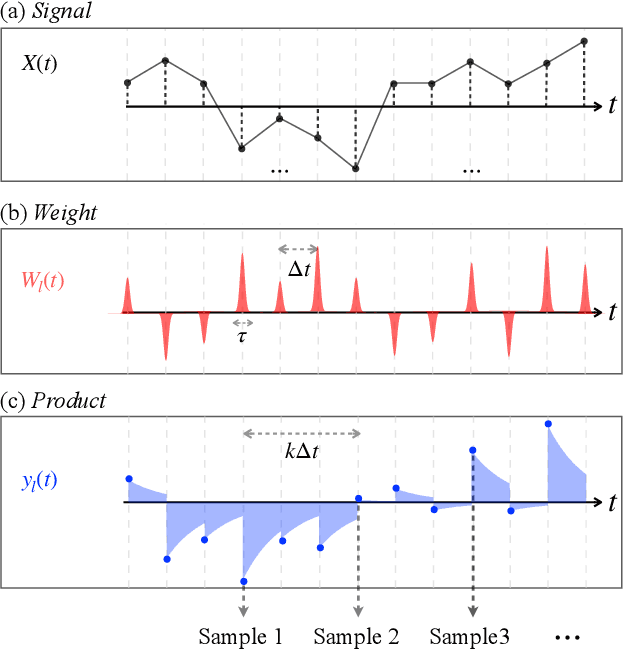
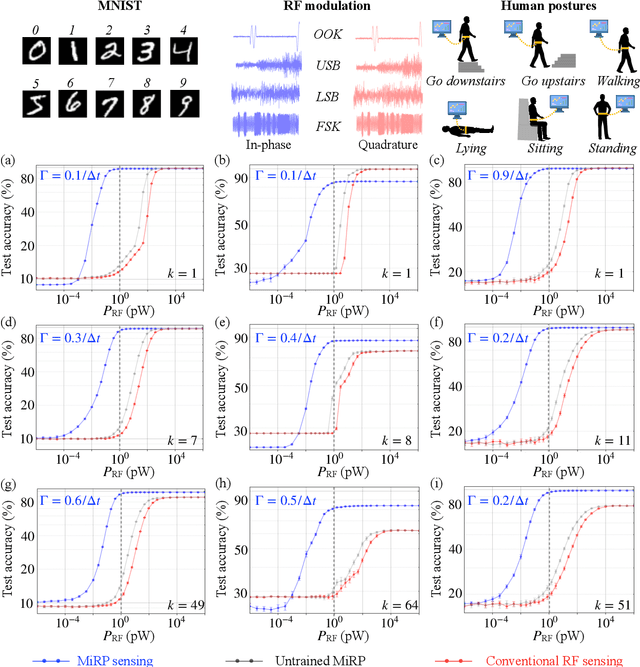
Radio-frequency (RF) sensing enables long-range, high-resolution detection for applications such as radar and wireless communication. RF photonic sensing mitigates the bandwidth limitations and high transmission losses of electronic systems by transducing the detected RF signals into broadband optical carriers. However, these sensing systems remain limited by detector noise and Nyquist rate sampling with analog-to-digital converters, particularly under low-power and high-data rate conditions. To overcome these limitations, we introduce the micro-ring perceptron (MiRP) sensor, a physics-inspired AI framework that integrates the micro-ring (MiR) dynamics-based analog processor with a machine-learning-driven digital backend. By embedding the nonlinear optical dynamics of MiRs into an end-to-end architecture, MiRP sensing maps the input signal into a learned feature space for the subsequent digital neural network. The trick is to encode the entire temporal structure of the incoming signal into each output sample in order to enable effectively sub-Nyquist sampling without loss of task-relevant information. Evaluations of three target classification datasets demonstrate the performance advantages of MiRP sensing. For example, on MNIST, MiRP detection achieves $94\pm0.1$\% accuracy at $1/49$ the Nyquist rate at the input RF signal of $1$~ pW, compared to $11\pm0.4$\% for the conventional RF detection method. Thus, our sensor framework provides a robust and efficient solution for the detection of low-power and high-speed signals in real-world sensing applications.

Quantum-secure multiparty deep learning

Secure multiparty computation enables the joint evaluation of multivariate functions across distributed users while ensuring the privacy of their local inputs. This field has become increasingly urgent due to the exploding demand for computationally intensive deep learning inference. These computations are typically offloaded to cloud computing servers, leading to vulnerabilities that can compromise the security of the clients' data. To solve this problem, we introduce a linear algebra engine that leverages the quantum nature of light for information-theoretically secure multiparty computation using only conventional telecommunication components. We apply this linear algebra engine to deep learning and derive rigorous upper bounds on the information leakage of both the deep neural network weights and the client's data via the Holevo and the Cram\'er-Rao bounds, respectively. Applied to the MNIST classification task, we obtain test accuracies exceeding $96\%$ while leaking less than $0.1$ bits per weight symbol and $0.01$ bits per data symbol. This weight leakage is an order of magnitude below the minimum bit precision required for accurate deep learning using state-of-the-art quantization techniques. Our work lays the foundation for practical quantum-secure computation and unlocks secure cloud deep learning as a field.

Deterministic fast and stable phase retrieval in multiple dimensions

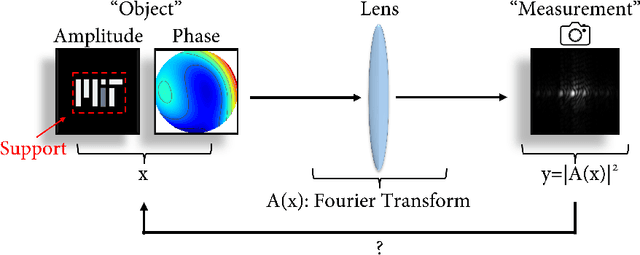
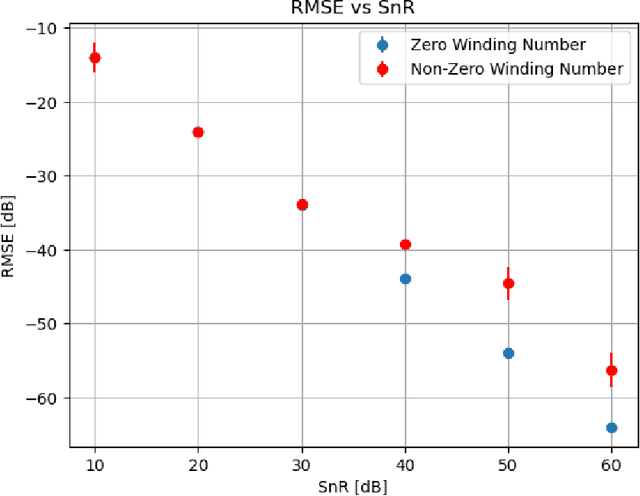
We present the first phase retrieval algorithm guaranteed to solve the multidimensional phase retrieval problem in polynomial arithmetic complexity without prior information. The method successfully terminates in O(N log(N)) operations for Fourier measurements with cardinality N. The algorithm is guaranteed to succeed for a large class of objects, which we term "Schwarz objects". We further present an easy-to-calculate and well-conditioned diagonal operator that transforms any feasible phase-retrieval instance into one that is solved by our method. We derive our method by combining techniques from classical complex analysis, algebraic topology, and modern numerical analysis. Concretely, we pose the phase retrieval problem as a multiplicative Cousin problem, construct an approximate solution using a modified integral used for the Schwarz problem, and refine the approximate solution to an exact solution via standard optimization methods. We present numerical experimentation demonstrating our algorithm's performance and its superiority to existing method. Finally, we demonstrate that our method is robust against Gaussian noise.

Dynamic Inhomogeneous Quantum Resource Scheduling with Reinforcement Learning

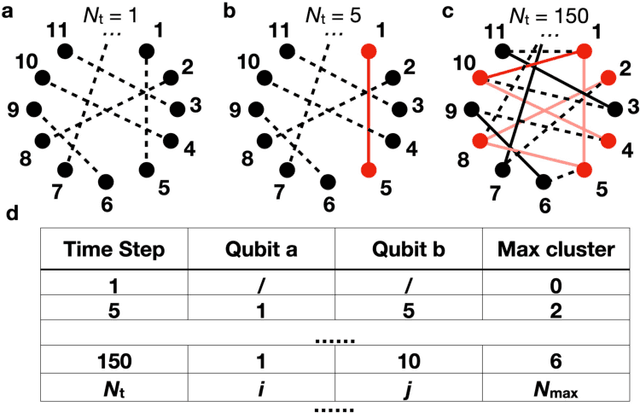
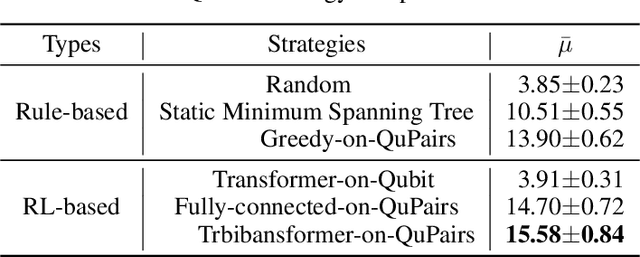
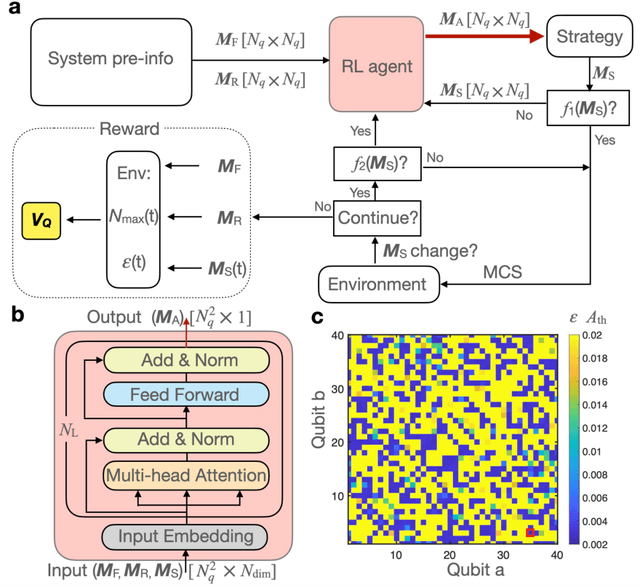
A central challenge in quantum information science and technology is achieving real-time estimation and feedforward control of quantum systems. This challenge is compounded by the inherent inhomogeneity of quantum resources, such as qubit properties and controls, and their intrinsically probabilistic nature. This leads to stochastic challenges in error detection and probabilistic outcomes in processes such as heralded remote entanglement. Given these complexities, optimizing the construction of quantum resource states is an NP-hard problem. In this paper, we address the quantum resource scheduling issue by formulating the problem and simulating it within a digitized environment, allowing the exploration and development of agent-based optimization strategies. We employ reinforcement learning agents within this probabilistic setting and introduce a new framework utilizing a Transformer model that emphasizes self-attention mechanisms for pairs of qubits. This approach facilitates dynamic scheduling by providing real-time, next-step guidance. Our method significantly improves the performance of quantum systems, achieving more than a 3$\times$ improvement over rule-based agents, and establishes an innovative framework that improves the joint design of physical and control systems for quantum applications in communication, networking, and computing.

Frequency-Encoded Deep Learning with Speed-of-Light Dominated Latency

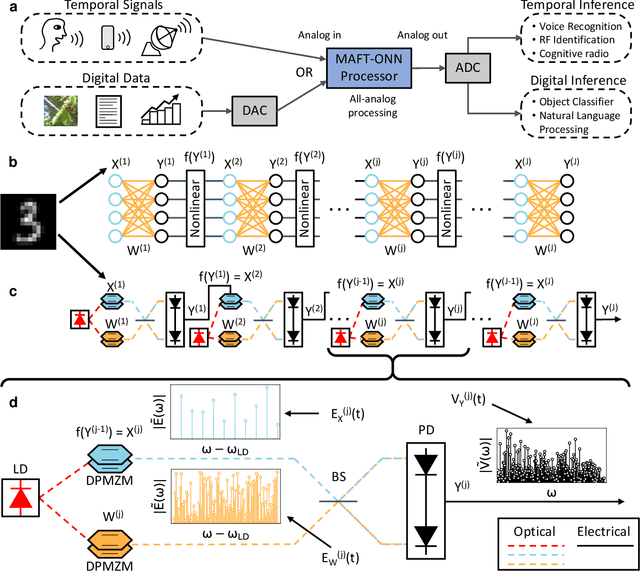
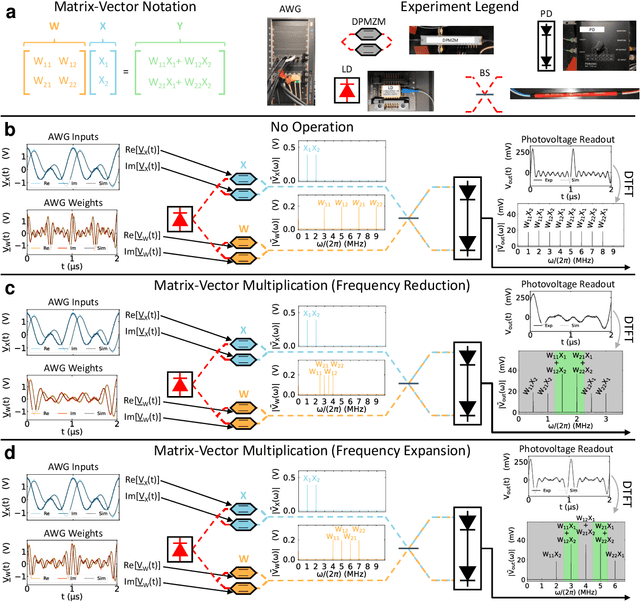
The ability of deep neural networks to perform complex tasks more accurately than manually-crafted solutions has created a substantial demand for more complex models processing larger amounts of data. However, the traditional computing architecture has reached a bottleneck in processing performance due to data movement from memory to computing. Considerable efforts have been made towards custom hardware acceleration, among which are optical neural networks (ONNs). These excel at energy efficient linear operations but struggle with scalability and the integration of linear and nonlinear functions. Here, we introduce our multiplicative analog frequency transform optical neural network (MAFT-ONN) that encodes the data in the frequency domain to compute matrix-vector products in a single-shot using a single photoelectric multiplication, and then implements the nonlinear activation for all neurons using a single electro-optic modulator. We experimentally demonstrate a 3-layer DNN with our architecture using a simple hardware setup assembled with commercial components. Additionally, this is the first DNN hardware accelerator suitable for analog inference of temporal waveforms like voice or radio signals, achieving bandwidth-limited throughput and speed-of-light limited latency. Our results demonstrate a highly scalable ONN with a straightforward path to surpassing the current computing bottleneck, in addition to enabling new possibilities for high-performance analog deep learning of temporal waveforms.

Single-Shot Optical Neural Network

As deep neural networks (DNNs) grow to solve increasingly complex problems, they are becoming limited by the latency and power consumption of existing digital processors. 'Weight-stationary' analog optical and electronic hardware has been proposed to reduce the compute resources required by DNNs by eliminating expensive weight updates; however, with scalability limited to an input vector length $K$ of hundreds of elements. Here, we present a scalable, single-shot-per-layer weight-stationary optical processor that leverages the advantages of free-space optics for passive optical copying and large-scale distribution of an input vector and integrated optoelectronics for static, reconfigurable weighting and the nonlinearity. We propose an optimized near-term CMOS-compatible system with $K = 1,000$ and beyond, and we calculate its theoretical total latency ($\sim$10 ns), energy consumption ($\sim$10 fJ/MAC) and throughput ($\sim$petaMAC/s) per layer. We also experimentally test DNN classification accuracy with single-shot analog optical encoding, copying and weighting of the MNIST handwritten digit dataset in a proof-of-concept system, achieving 94.7% (similar to the ground truth accuracy of 96.3%) without retraining on the hardware or data preprocessing. Lastly, we determine the upper bound on throughput of our system ($\sim$0.9 exaMAC/s), set by the maximum optical bandwidth before significant loss of accuracy. This joint use of wide spectral and spatial bandwidths enables highly efficient computing for next-generation DNNs.

Quantum algorithms for group convolution, cross-correlation, and equivariant transformations

Group convolutions and cross-correlations, which are equivariant to the actions of group elements, are commonly used in mathematics to analyze or take advantage of symmetries inherent in a given problem setting. Here, we provide efficient quantum algorithms for performing linear group convolutions and cross-correlations on data stored as quantum states. Runtimes for our algorithms are logarithmic in the dimension of the group thus offering an exponential speedup compared to classical algorithms when input data is provided as a quantum state and linear operations are well conditioned. Motivated by the rich literature on quantum algorithms for solving algebraic problems, our theoretical framework opens a path for quantizing many algorithms in machine learning and numerical methods that employ group operations.