Neural Networks for Programming Quantum Annealers

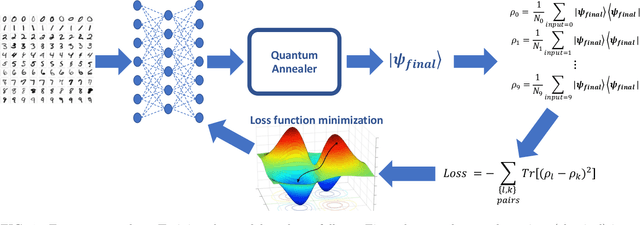
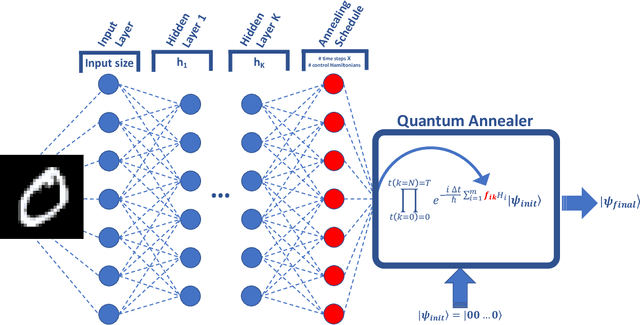
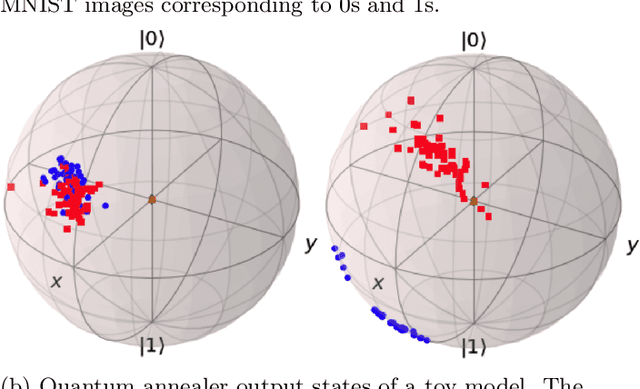
Quantum machine learning has the potential to enable advances in artificial intelligence, such as solving problems intractable on classical computers. Some fundamental ideas behind quantum machine learning are similar to kernel methods in classical machine learning. Both process information by mapping it into high-dimensional vector spaces without explicitly calculating their numerical values. We explore a setup for performing classification on labeled classical datasets, consisting of a classical neural network connected to a quantum annealer. The neural network programs the quantum annealer's controls and thereby maps the annealer's initial states into new states in the Hilbert space. The neural network's parameters are optimized to maximize the distance of states corresponding to inputs from different classes and minimize the distance between quantum states corresponding to the same class. Recent literature showed that at least some of the "learning" is due to the quantum annealer, connecting a small linear network to a quantum annealer and using it to learn small and linearly inseparable datasets. In this study, we consider a similar but not quite the same case, where a classical fully-fledged neural network is connected with a small quantum annealer. In such a setting, the fully-fledged classical neural-network already has built-in nonlinearity and learning power, and can already handle the classification problem alone, we want to see whether an additional quantum layer could boost its performance. We simulate this system to learn several common datasets, including those for image and sound recognition. We conclude that adding a small quantum annealer does not provide a significant benefit over just using a regular (nonlinear) classical neural network.

Joint Embedding Self-Supervised Learning in the Kernel Regime

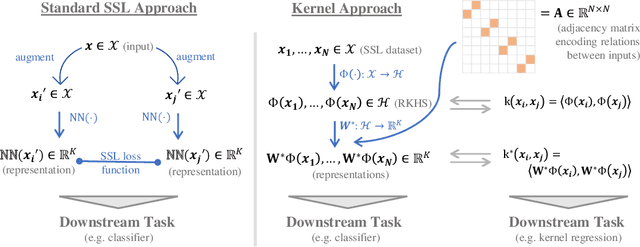
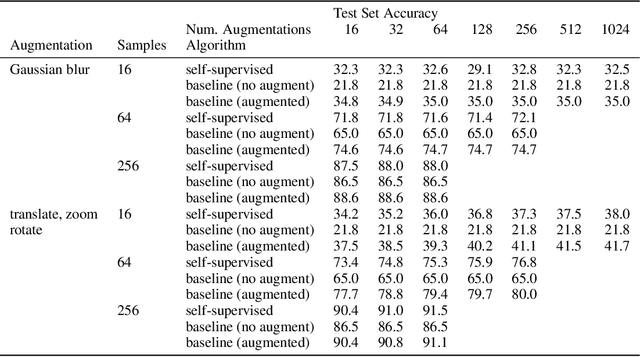
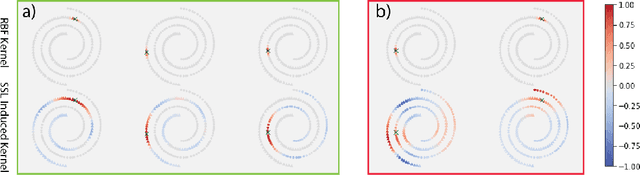
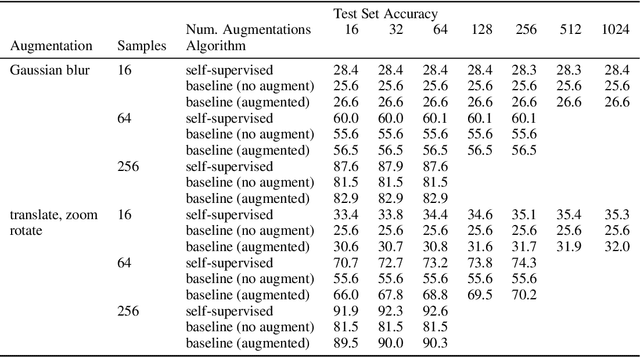
The fundamental goal of self-supervised learning (SSL) is to produce useful representations of data without access to any labels for classifying the data. Modern methods in SSL, which form representations based on known or constructed relationships between samples, have been particularly effective at this task. Here, we aim to extend this framework to incorporate algorithms based on kernel methods where embeddings are constructed by linear maps acting on the feature space of a kernel. In this kernel regime, we derive methods to find the optimal form of the output representations for contrastive and non-contrastive loss functions. This procedure produces a new representation space with an inner product denoted as the induced kernel which generally correlates points which are related by an augmentation in kernel space and de-correlates points otherwise. We analyze our kernel model on small datasets to identify common features of self-supervised learning algorithms and gain theoretical insights into their performance on downstream tasks.

projUNN: efficient method for training deep networks with unitary matrices

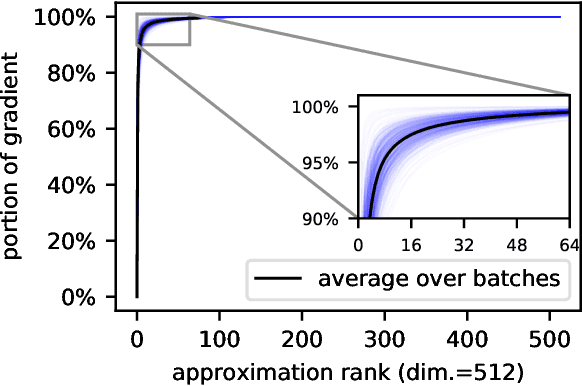
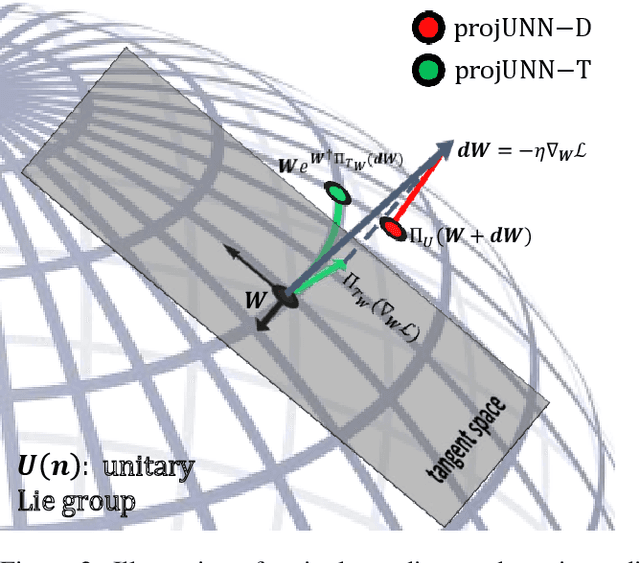
In learning with recurrent or very deep feed-forward networks, employing unitary matrices in each layer can be very effective at maintaining long-range stability. However, restricting network parameters to be unitary typically comes at the cost of expensive parameterizations or increased training runtime. We propose instead an efficient method based on rank-$k$ updates -- or their rank-$k$ approximation -- that maintains performance at a nearly optimal training runtime. We introduce two variants of this method, named Direct (projUNN-D) and Tangent (projUNN-T) projected Unitary Neural Networks, that can parameterize full $N$-dimensional unitary or orthogonal matrices with a training runtime scaling as $O(kN^2)$. Our method either projects low-rank gradients onto the closest unitary matrix (projUNN-T) or transports unitary matrices in the direction of the low-rank gradient (projUNN-D). Even in the fastest setting ($k=1$), projUNN is able to train a model's unitary parameters to reach comparable performances against baseline implementations. By integrating our projUNN algorithm into both recurrent and convolutional neural networks, our models can closely match or exceed benchmarked results from state-of-the-art algorithms.

Quantum algorithms for group convolution, cross-correlation, and equivariant transformations

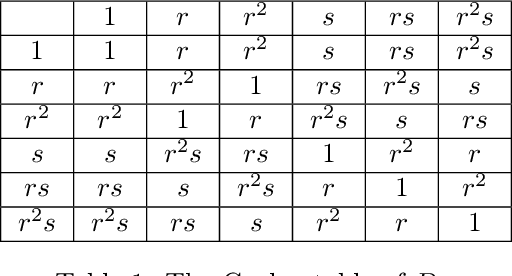
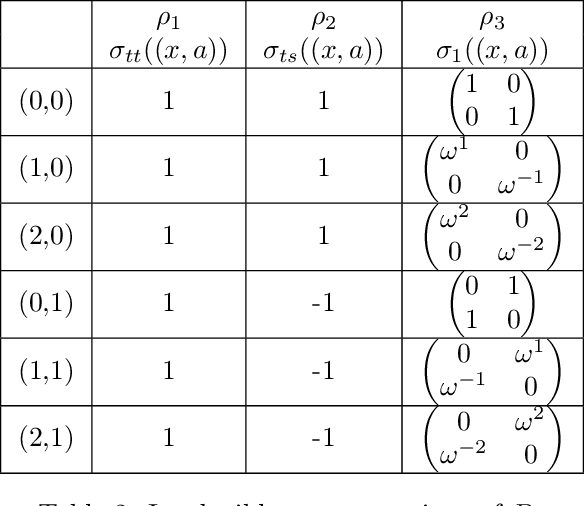
Group convolutions and cross-correlations, which are equivariant to the actions of group elements, are commonly used in mathematics to analyze or take advantage of symmetries inherent in a given problem setting. Here, we provide efficient quantum algorithms for performing linear group convolutions and cross-correlations on data stored as quantum states. Runtimes for our algorithms are logarithmic in the dimension of the group thus offering an exponential speedup compared to classical algorithms when input data is provided as a quantum state and linear operations are well conditioned. Motivated by the rich literature on quantum algorithms for solving algebraic problems, our theoretical framework opens a path for quantizing many algorithms in machine learning and numerical methods that employ group operations.

A quantum algorithm for training wide and deep classical neural networks

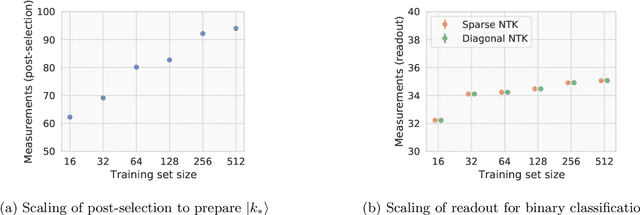
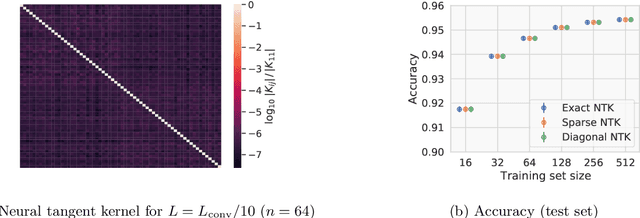
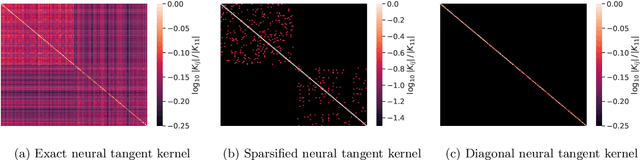
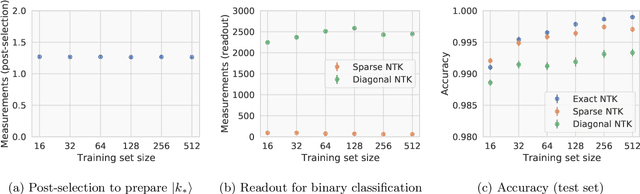
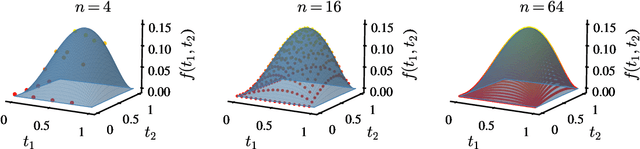
Given the success of deep learning in classical machine learning, quantum algorithms for traditional neural network architectures may provide one of the most promising settings for quantum machine learning. Considering a fully-connected feedforward neural network, we show that conditions amenable to classical trainability via gradient descent coincide with those necessary for efficiently solving quantum linear systems. We propose a quantum algorithm to approximately train a wide and deep neural network up to $O(1/n)$ error for a training set of size $n$ by performing sparse matrix inversion in $O(\log n)$ time. To achieve an end-to-end exponential speedup over gradient descent, the data distribution must permit efficient state preparation and readout. We numerically demonstrate that the MNIST image dataset satisfies such conditions; moreover, the quantum algorithm matches the accuracy of the fully-connected network. Beyond the proven architecture, we provide empirical evidence for $O(\log n)$ training of a convolutional neural network with pooling.

Quantum Earth Mover's Distance: A New Approach to Learning Quantum Data

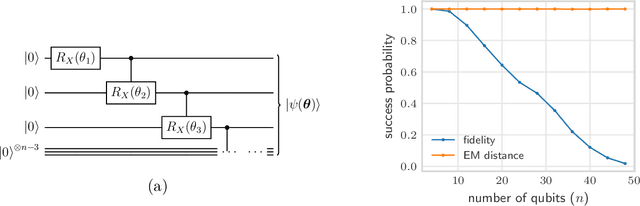
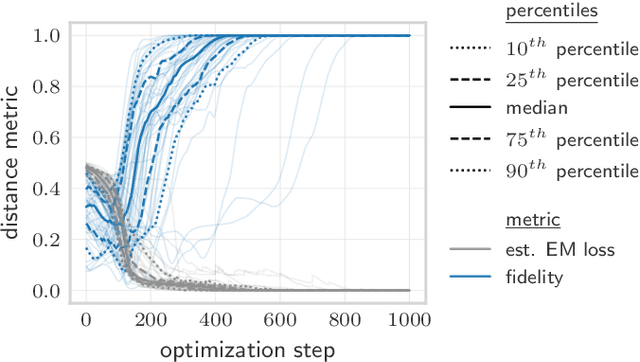
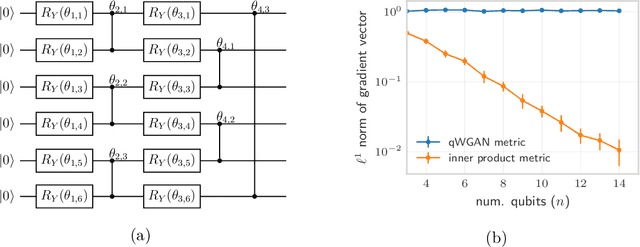
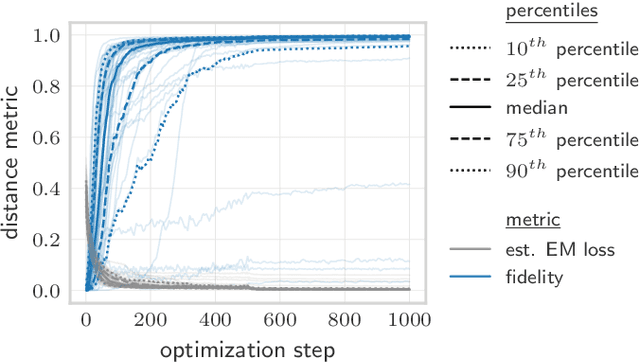
Quantifying how far the output of a learning algorithm is from its target is an essential task in machine learning. However, in quantum settings, the loss landscapes of commonly used distance metrics often produce undesirable outcomes such as poor local minima and exponentially decaying gradients. As a new approach, we consider here the quantum earth mover's (EM) or Wasserstein-1 distance, recently proposed in [De Palma et al., arXiv:2009.04469] as a quantum analog to the classical EM distance. We show that the quantum EM distance possesses unique properties, not found in other commonly used quantum distance metrics, that make quantum learning more stable and efficient. We propose a quantum Wasserstein generative adversarial network (qWGAN) which takes advantage of the quantum EM distance and provides an efficient means of performing learning on quantum data. Our qWGAN requires resources polynomial in the number of qubits, and our numerical experiments demonstrate that it is capable of learning a diverse set of quantum data.

Adversarial robustness guarantees for random deep neural networks

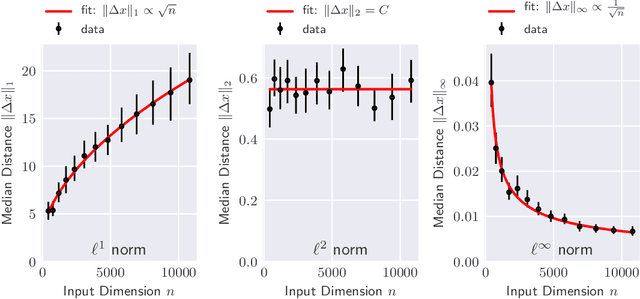
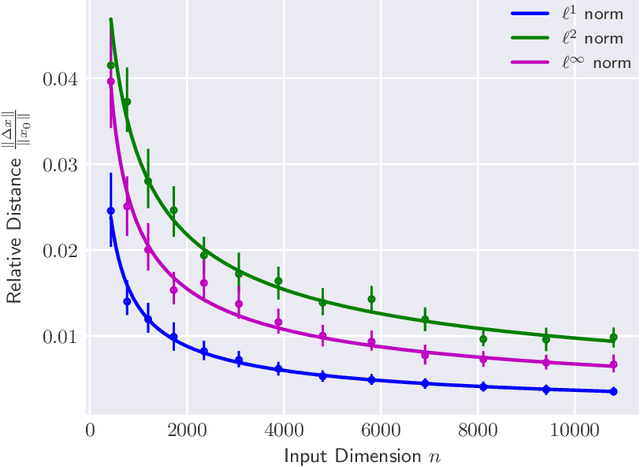
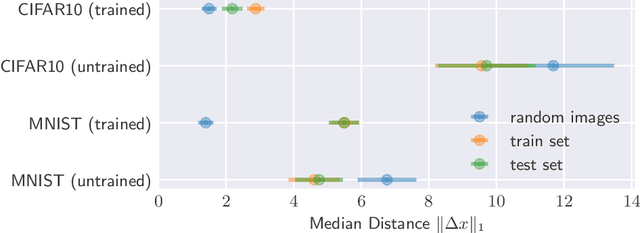
The reliability of most deep learning algorithms is fundamentally challenged by the existence of adversarial examples, which are incorrectly classified inputs that are extremely close to a correctly classified input. We study adversarial examples for deep neural networks with random weights and biases and prove that the $\ell^1$ distance of any given input from the classification boundary scales at least as $\sqrt{n}$, where $n$ is the dimension of the input. We also extend our proof to cover all the $\ell^p$ norms. Our results constitute a fundamental advance in the study of adversarial examples, and encompass a wide variety of architectures, which include any combination of convolutional or fully connected layers with skipped connections and pooling. We validate our results with experiments on both random deep neural networks and deep neural networks trained on the MNIST and CIFAR10 datasets. Given the results of our experiments on MNIST and CIFAR10, we conjecture that the proof of our adversarial robustness guarantee can be extended to trained deep neural networks. This extension will open the way to a thorough theoretical study of neural network robustness by classifying the relation between network architecture and adversarial distance.

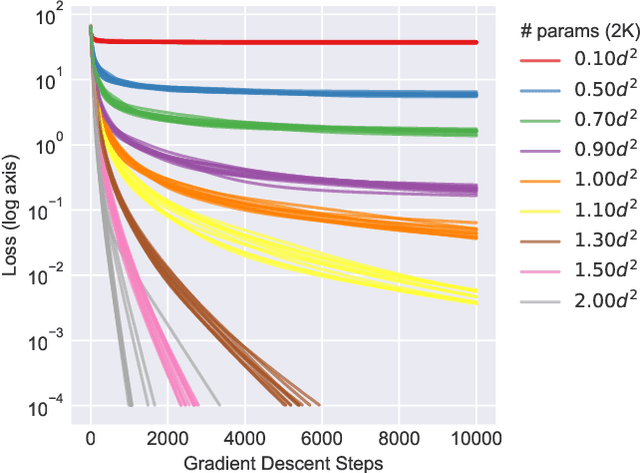
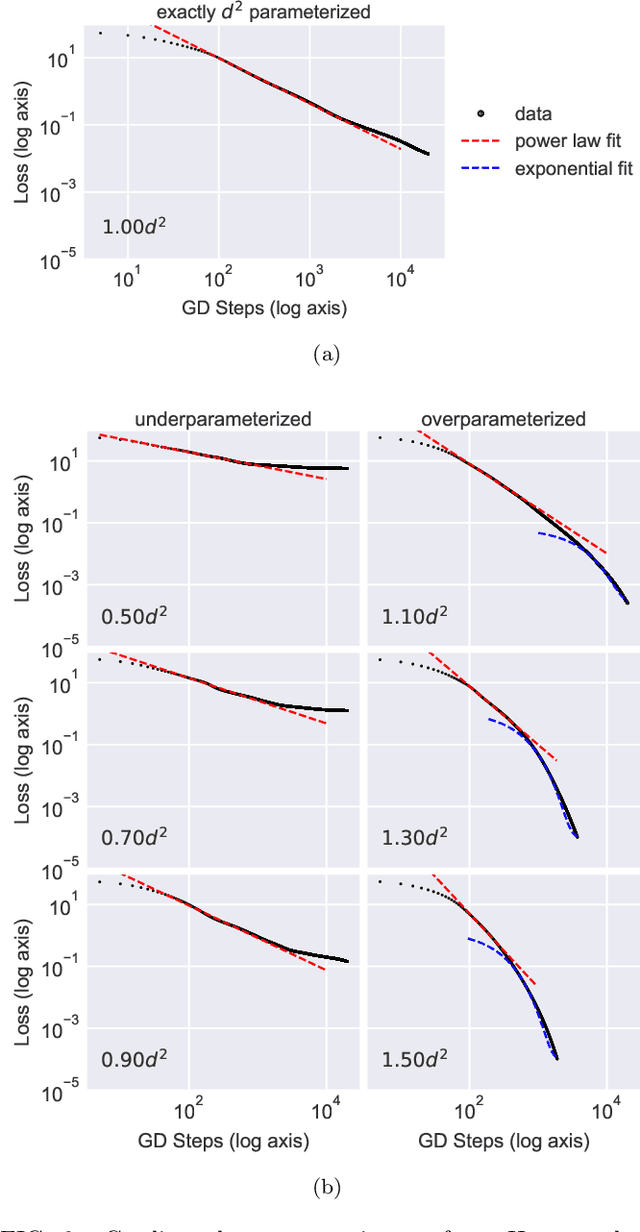
Learning Unitaries by Gradient Descent

We study the hardness of learning unitary transformations in $U(d)$ via gradient descent on time parameters of alternating operator sequences. We provide numerical evidence that, despite the non-convex nature of the loss landscape, gradient descent always converges to the target unitary when the sequence contains $d^2$ or more parameters. Rates of convergence indicate a "computational phase transition." With less than $d^2$ parameters, gradient descent converges to a sub-optimal solution, whereas with more than $d^2$ parameters, gradient descent converges exponentially to an optimal solution.

Deep neural networks are biased towards simple functions

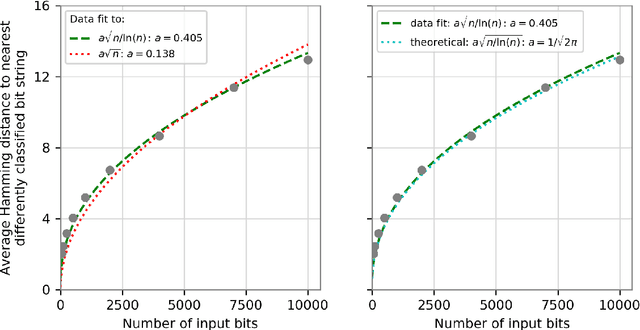
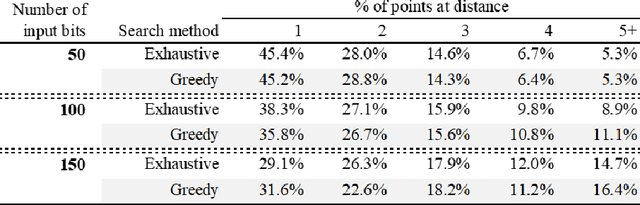
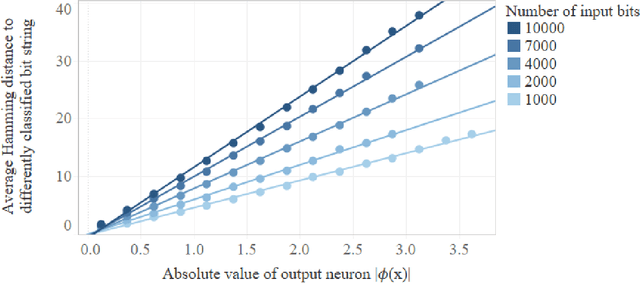
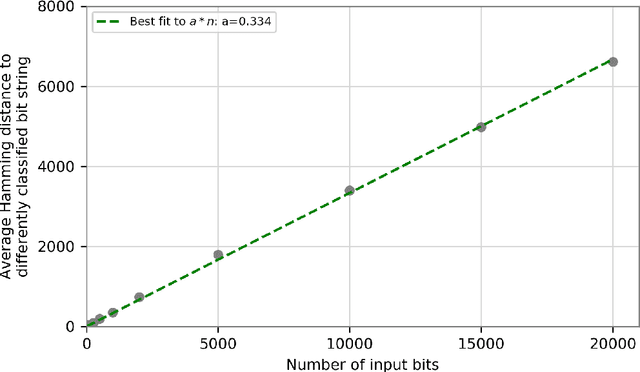
We prove that the binary classifiers of bit strings generated by random wide deep neural networks are biased towards simple functions. The simplicity is captured by the following two properties. For any given input bit string, the average Hamming distance of the closest input bit string with a different classification is at least $\sqrt{n\left/\left(2\pi\ln n\right)\right.}$, where $n$ is the length of the string. Moreover, if the bits of the initial string are flipped randomly, the average number of flips required to change the classification grows linearly with $n$. On the contrary, for a uniformly random binary classifier, the average Hamming distance of the closest input bit string with a different classification is one, and the average number of random flips required to change the classification is two. These results are confirmed by numerical experiments on deep neural networks with two hidden layers, and settle the conjecture stating that random deep neural networks are biased towards simple functions. The conjecture that random deep neural networks are biased towards simple functions was proposed and numerically explored in [Valle P\'erez et al., arXiv:1805.08522] to explain the unreasonably good generalization properties of deep learning algorithms. By providing a precise characterization of the form of this bias towards simplicity, our results open the way to a rigorous proof of the generalization properties of deep learning algorithms in real-world scenarios.

Continuous-variable quantum neural networks

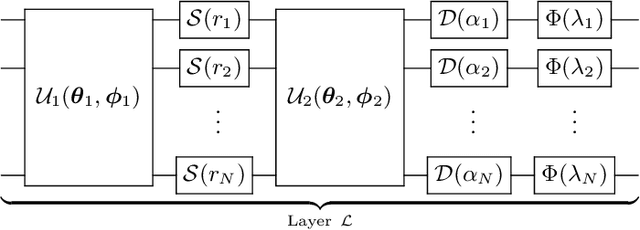
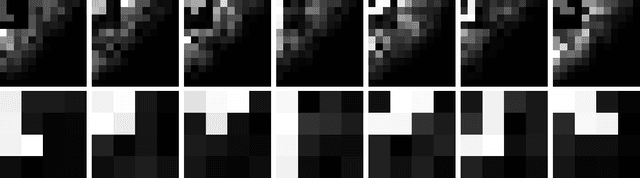
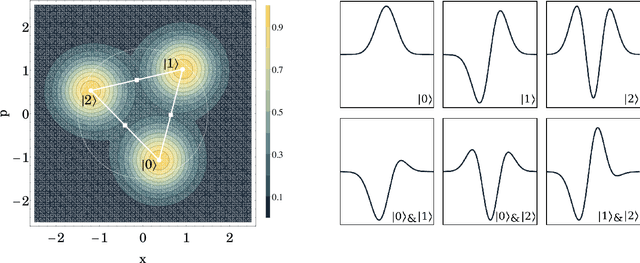
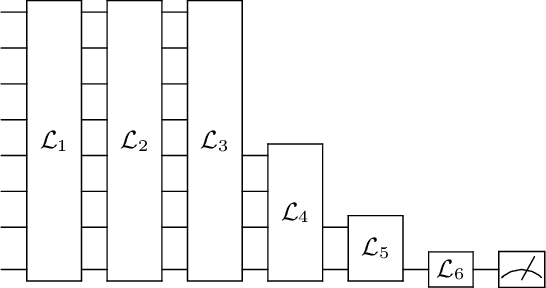
We introduce a general method for building neural networks on quantum computers. The quantum neural network is a variational quantum circuit built in the continuous-variable (CV) architecture, which encodes quantum information in continuous degrees of freedom such as the amplitudes of the electromagnetic field. This circuit contains a layered structure of continuously parameterized gates which is universal for CV quantum computation. Affine transformations and nonlinear activation functions, two key elements in neural networks, are enacted in the quantum network using Gaussian and non-Gaussian gates, respectively. The non-Gaussian gates provide both the nonlinearity and the universality of the model. Due to the structure of the CV model, the CV quantum neural network can encode highly nonlinear transformations while remaining completely unitary. We show how a classical network can be embedded into the quantum formalism and propose quantum versions of various specialized model such as convolutional, recurrent, and residual networks. Finally, we present numerous modeling experiments built with the Strawberry Fields software library. These experiments, including a classifier for fraud detection, a network which generates Tetris images, and a hybrid classical-quantum autoencoder, demonstrate the capability and adaptability of CV quantum neural networks.