Inference, interference and invariance: How the Quantum Fourier Transform can help to learn from data

How can we take inspiration from a typical quantum algorithm to design heuristics for machine learning? A common blueprint, used from Deutsch-Josza to Shor's algorithm, is to place labeled information in superposition via an oracle, interfere in Fourier space, and measure. In this paper, we want to understand how this interference strategy can be used for inference, i.e. to generalize from finite data samples to a ground truth. Our investigative framework is built around the Hidden Subgroup Problem (HSP), which we transform into a learning task by replacing the oracle with classical training data. The standard quantum algorithm for solving the HSP uses the Quantum Fourier Transform to expose an invariant subspace, i.e., a subset of Hilbert space in which the hidden symmetry is manifest. Based on this insight, we propose an inference principle that "compares" the data to this invariant subspace, and suggest a concrete implementation via overlaps of quantum states. We hope that this leads to well-motivated quantum heuristics that can leverage symmetries for machine learning applications.

Better than classical? The subtle art of benchmarking quantum machine learning models

Benchmarking models via classical simulations is one of the main ways to judge ideas in quantum machine learning before noise-free hardware is available. However, the huge impact of the experimental design on the results, the small scales within reach today, as well as narratives influenced by the commercialisation of quantum technologies make it difficult to gain robust insights. To facilitate better decision-making we develop an open-source package based on the PennyLane software framework and use it to conduct a large-scale study that systematically tests 12 popular quantum machine learning models on 6 binary classification tasks used to create 160 individual datasets. We find that overall, out-of-the-box classical machine learning models outperform the quantum classifiers. Moreover, removing entanglement from a quantum model often results in as good or better performance, suggesting that "quantumness" may not be the crucial ingredient for the small learning tasks considered here. Our benchmarks also unlock investigations beyond simplistic leaderboard comparisons, and we identify five important questions for quantum model design that follow from our results.

Quantum machine learning models are kernel methods

With near-term quantum devices available and the race for fault-tolerant quantum computers in full swing, researchers became interested in the question of what happens if we replace a machine learning model with a quantum circuit. While such "quantum models" are sometimes called "quantum neural networks", it has been repeatedly noted that their mathematical structure is actually much more closely related to kernel methods: they analyse data in high-dimensional Hilbert spaces to which we only have access through inner products revealed by measurements. This technical manuscript summarises, formalises and extends the link by systematically rephrasing quantum models as a kernel method. It shows that most near-term and fault-tolerant quantum models can be replaced by a general support vector machine whose kernel computes distances between data-encoding quantum states. In particular, kernel-based training is guaranteed to find better or equally good quantum models than variational circuit training. Overall, the kernel perspective of quantum machine learning tells us that the way that data is encoded into quantum states is the main ingredient that can potentially set quantum models apart from classical machine learning models.

The effect of data encoding on the expressive power of variational quantum machine learning models

Quantum computers can be used for supervised learning by treating parametrised quantum circuits as models that map data inputs to predictions. While a lot of work has been done to investigate practical implications of this approach, many important theoretical properties of these models remain unknown. Here we investigate how the strategy with which data is encoded into the model influences the expressive power of parametrised quantum circuits as function approximators. We show that one can naturally write a quantum model as a partial Fourier series in the data, where the accessible frequencies are determined by the nature of the data encoding gates in the circuit. By repeating simple data encoding gates multiple times, quantum models can access increasingly rich frequency spectra. We show that there exist quantum models which can realise all possible sets of Fourier coefficients, and therefore, if the accessible frequency spectrum is asymptotically rich enough, such models are universal function approximators.

Transfer learning in hybrid classical-quantum neural networks

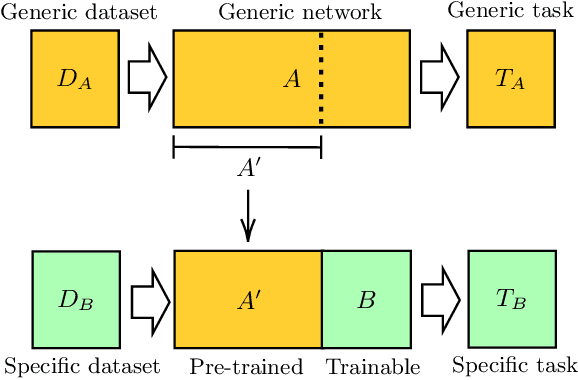
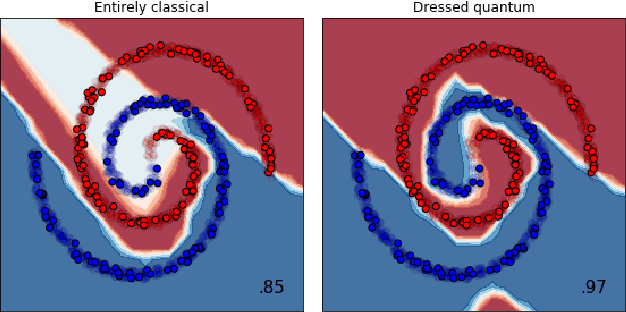
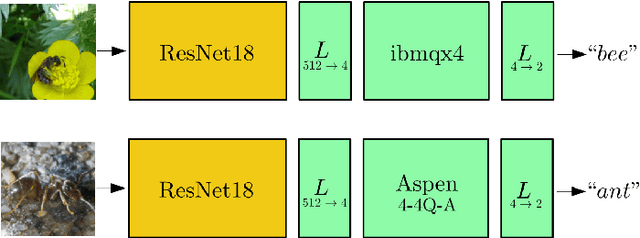
We extend the concept of transfer learning, widely applied in modern machine learning algorithms, to the emerging context of hybrid neural networks composed of classical and quantum elements. We propose different implementations of hybrid transfer learning, but we focus mainly on the paradigm in which a pre-trained classical network is modified and augmented by a final variational quantum circuit. This approach is particularly attractive in the current era of intermediate-scale quantum technology since it allows to optimally pre-process high dimensional data (e.g., images) with any state-of-the-art classical network and to embed a select set of highly informative features into a quantum processor. We present several proof-of-concept examples of the convenient application of quantum transfer learning for image recognition and quantum state classification. We use the cross-platform software library PennyLane to experimentally test a high-resolution image classifier with two different quantum computers, respectively provided by IBM and Rigetti.

Stochastic gradient descent for hybrid quantum-classical optimization

Within the context of hybrid quantum-classical optimization, gradient descent based optimizers typically require the evaluation of expectation values with respect to the outcome of parameterized quantum circuits. In this work, we explore the significant consequences of the simple observation that the estimation of these quantities on quantum hardware is a form of stochastic gradient descent optimization. We formalize this notion, which allows us to show that in many relevant cases, including VQE, QAOA and certain quantum classifiers, estimating expectation values with $k$ measurement outcomes results in optimization algorithms whose convergence properties can be rigorously well understood, for any value of $k$. In fact, even using single measurement outcomes for the estimation of expectation values is sufficient. Moreover, in many settings the required gradients can be expressed as linear combinations of expectation values -- originating, e.g., from a sum over local terms of a Hamiltonian, a parameter shift rule, or a sum over data-set instances -- and we show that in these cases $k$-shot expectation value estimation can be combined with sampling over terms of the linear combination, to obtain "doubly stochastic" gradient descent optimizers. For all algorithms we prove convergence guarantees, providing a framework for the derivation of rigorous optimization results in the context of near-term quantum devices. Additionally, we explore numerically these methods on benchmark VQE, QAOA and quantum-enhanced machine learning tasks and show that treating the stochastic settings as hyper-parameters allows for state-of-the-art results with significantly fewer circuit executions and measurements.

PennyLane: Automatic differentiation of hybrid quantum-classical computations

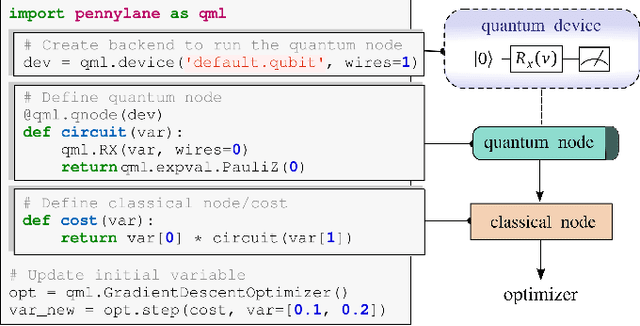
PennyLane is a Python 3 software framework for optimization and machine learning of quantum and hybrid quantum-classical computations. The library provides a unified architecture for near-term quantum computing devices, supporting both qubit and continuous-variable paradigms. PennyLane's core feature is the ability to compute gradients of variational quantum circuits in a way that is compatible with classical techniques such as backpropagation. PennyLane thus extends the automatic differentiation algorithms common in optimization and machine learning to include quantum and hybrid computations. A plugin system makes the framework compatible with any gate-based quantum simulator or hardware. We provide plugins for StrawberryFields and ProjectQ (including a IBMQE device interface). PennyLane can be used for the optimization of variational quantum eigensolvers, quantum approximate optimization, quantum machine learning models, and many other applications.

Continuous-variable quantum neural networks

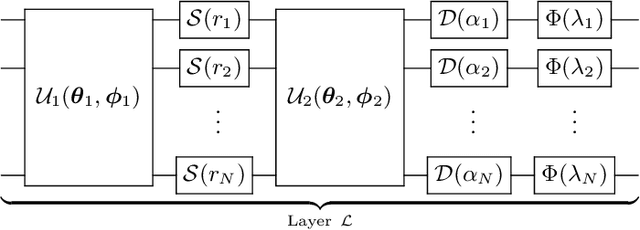
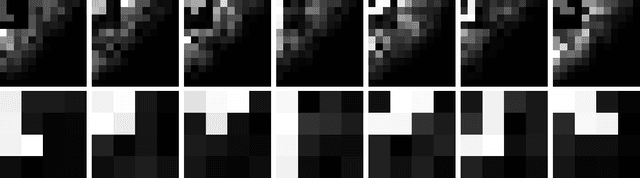
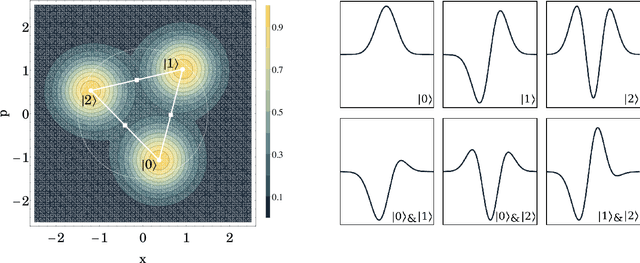
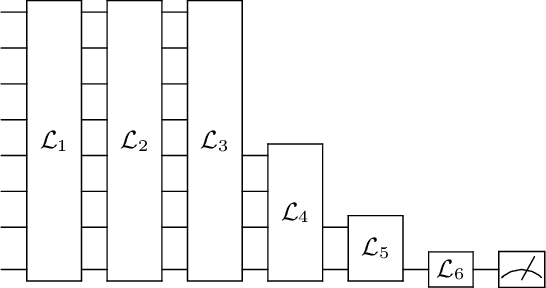
We introduce a general method for building neural networks on quantum computers. The quantum neural network is a variational quantum circuit built in the continuous-variable (CV) architecture, which encodes quantum information in continuous degrees of freedom such as the amplitudes of the electromagnetic field. This circuit contains a layered structure of continuously parameterized gates which is universal for CV quantum computation. Affine transformations and nonlinear activation functions, two key elements in neural networks, are enacted in the quantum network using Gaussian and non-Gaussian gates, respectively. The non-Gaussian gates provide both the nonlinearity and the universality of the model. Due to the structure of the CV model, the CV quantum neural network can encode highly nonlinear transformations while remaining completely unitary. We show how a classical network can be embedded into the quantum formalism and propose quantum versions of various specialized model such as convolutional, recurrent, and residual networks. Finally, we present numerous modeling experiments built with the Strawberry Fields software library. These experiments, including a classifier for fraud detection, a network which generates Tetris images, and a hybrid classical-quantum autoencoder, demonstrate the capability and adaptability of CV quantum neural networks.

Quantum ensembles of quantum classifiers

Quantum machine learning witnesses an increasing amount of quantum algorithms for data-driven decision making, a problem with potential applications ranging from automated image recognition to medical diagnosis. Many of those algorithms are implementations of quantum classifiers, or models for the classification of data inputs with a quantum computer. Following the success of collective decision making with ensembles in classical machine learning, this paper introduces the concept of quantum ensembles of quantum classifiers. Creating the ensemble corresponds to a state preparation routine, after which the quantum classifiers are evaluated in parallel and their combined decision is accessed by a single-qubit measurement. This framework naturally allows for exponentially large ensembles in which -- similar to Bayesian learning -- the individual classifiers do not have to be trained. As an example, we analyse an exponentially large quantum ensemble in which each classifier is weighed according to its performance in classifying the training data, leading to new results for quantum as well as classical machine learning.

Simulating a perceptron on a quantum computer

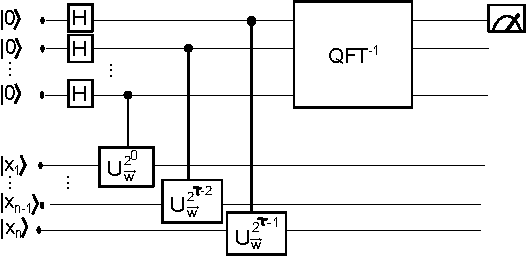
Perceptrons are the basic computational unit of artificial neural networks, as they model the activation mechanism of an output neuron due to incoming signals from its neighbours. As linear classifiers, they play an important role in the foundations of machine learning. In the context of the emerging field of quantum machine learning, several attempts have been made to develop a corresponding unit using quantum information theory. Based on the quantum phase estimation algorithm, this paper introduces a quantum perceptron model imitating the step-activation function of a classical perceptron. This scheme requires resources in $\mathcal{O}(n)$ (where $n$ is the size of the input) and promises efficient applications for more complex structures such as trainable quantum neural networks.