Ilya Sinayskiy
Hybrid Genetic Optimisation for Quantum Feature Map Design
Feb 06, 2023Abstract:Kernel methods are an important class of techniques in machine learning. To be effective, good feature maps are crucial for mapping non-linearly separable input data into a higher dimensional (feature) space, thus allowing the data to be linearly separable in feature space. Previous work has shown that quantum feature map design can be automated for a given dataset using NSGA-II, a genetic algorithm, while both minimizing circuit size and maximizing classification accuracy. However, the evaluation of the accuracy achieved by a candidate feature map is costly. In this work, we demonstrate the suitability of kernel-target alignment as a substitute for accuracy in genetic algorithm-based quantum feature map design. Kernel-target alignment is faster to evaluate than accuracy and doesn't require some data points to be reserved for its evaluation. To further accelerate the evaluation of genetic fitness, we provide a method to approximate kernel-target alignment. To improve kernel-target alignment and root mean squared error, the final trainable parameters of the generated circuits are further trained using COBYLA to determine whether a hybrid approach applying conventional circuit parameter training can easily complement the genetic structure optimization approach. A total of eight new approaches are compared to the original across nine varied binary classification problems from the UCI machine learning repository, showing that kernel-target alignment and its approximation produce feature map circuits enabling comparable accuracy to the previous work but with larger margins on training data (in excess of 20\% larger) that improve further with circuit parameter training.
Architecture representations for quantum convolutional neural networks
Oct 26, 2022Abstract:The Quantum Convolutional Neural Network (QCNN) is a quantum circuit model inspired by the architecture of Convolutional Neural Networks (CNNs). The success of CNNs is largely due to its ability to learn high level features from raw data rather than requiring manual feature design. Neural Architecture Search (NAS) continues this trend by learning network architecture, alleviating the need for its manual construction and have been able to generate state of the art models automatically. Search space design is a crucial step in NAS and there is currently no formal framework through which it can be achieved for QCNNs. In this work we provide such a framework by utilizing techniques from NAS to create an architectural representation for QCNNs that facilitate search space design and automatic model generation. This is done by specifying primitive operations, such as convolutions and pooling, in such a way that they can be dynamically stacked on top of each other to form different architectures. This way, QCNN search spaces can be created by controlling the sequence and hyperparameters of stacked primitives, allowing the capture of different design motifs. We show this by generating QCNNs that belong to a popular family of parametric quantum circuits, those resembling reverse binary trees. We then benchmark this family of models on a music genre classification dataset, GTZAN. Showing that alternating architecture impact model performance more than other modelling components such as choice of unitary ansatz and data encoding, resulting in a way to improve model performance without increasing its complexity. Finally we provide an open source python package that enable dynamic QCNN creation by system or hand, based off the work presented in this paper, facilitating search space design.
Simulating a perceptron on a quantum computer
Dec 11, 2014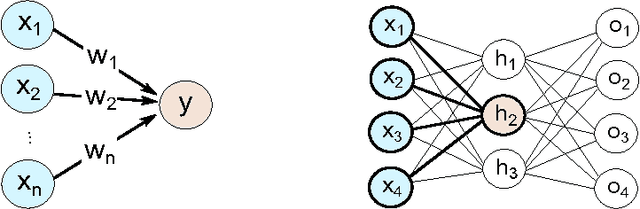
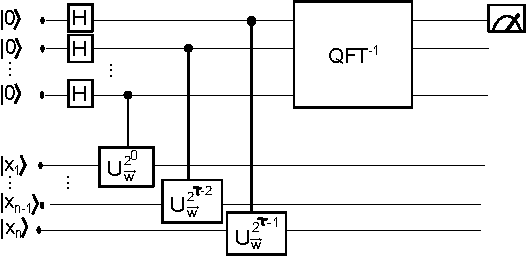

Abstract:Perceptrons are the basic computational unit of artificial neural networks, as they model the activation mechanism of an output neuron due to incoming signals from its neighbours. As linear classifiers, they play an important role in the foundations of machine learning. In the context of the emerging field of quantum machine learning, several attempts have been made to develop a corresponding unit using quantum information theory. Based on the quantum phase estimation algorithm, this paper introduces a quantum perceptron model imitating the step-activation function of a classical perceptron. This scheme requires resources in $\mathcal{O}(n)$ (where $n$ is the size of the input) and promises efficient applications for more complex structures such as trainable quantum neural networks.
* 11 pages, 6 figures, accepted by Physics Letters A
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge