Daniel K. Park
Scalable Neural Decoders for Practical Real-Time Quantum Error Correction
Oct 26, 2025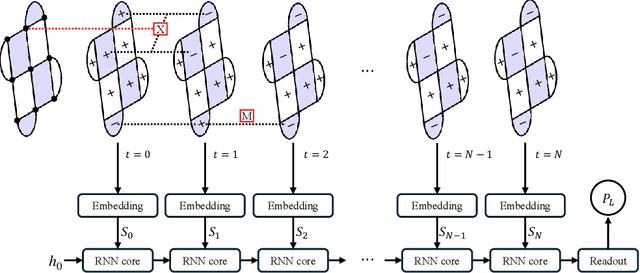

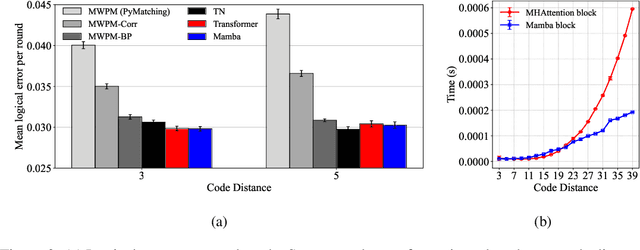
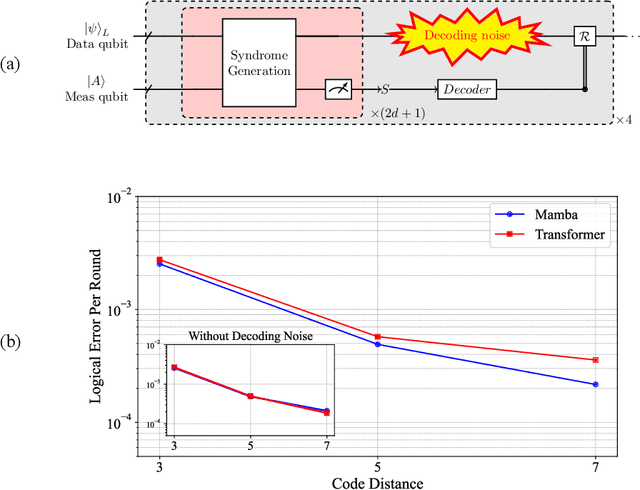
Abstract:Real-time, scalable, and accurate decoding is a critical component for realizing a fault-tolerant quantum computer. While Transformer-based neural decoders such as \textit{AlphaQubit} have demonstrated high accuracy, the computational complexity of their core attention mechanism, which scales as $\mathcal{O}(d^4)$ with code distance $d$, results in decoding speeds insufficient for practical real-time applications. In this work, we introduce and evaluate a \textit{Mamba}-based decoder, a state-space model with $\mathcal{O}(d^2)$ complexity. In memory experiments using Sycamore hardware data, our Mamba decoder matches the performance of its Transformer-based counterpart, providing that its superior efficiency does not come at the cost of performance. Crucially, in simulated real-time scenarios that account for decoder-induced noise, the Mamba decoder significantly outperforms the Transformer, exhibiting a higher error threshold of $0.0104$ compared to $0.0097$. These results demonstrate that Mamba decoders offer a compelling balance between speed and accuracy, making them a promising architecture for scalable, real-time quantum error correction.
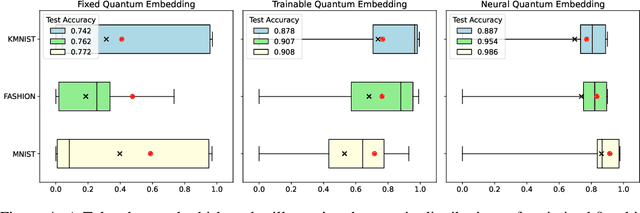
Multi-channel convolutional neural quantum embedding
Sep 26, 2025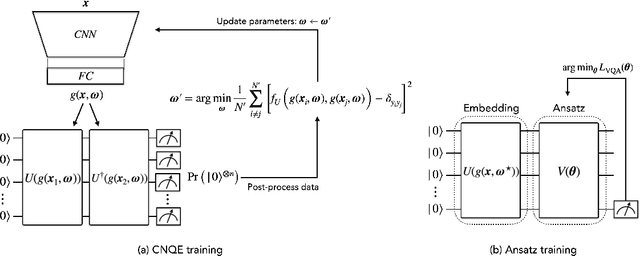
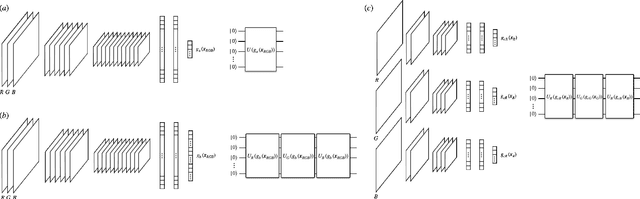
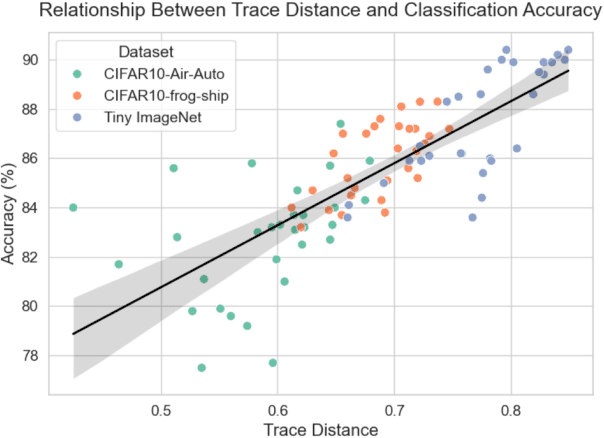
Abstract:Classification using variational quantum circuits is a promising frontier in quantum machine learning. Quantum supervised learning (QSL) applied to classical data using variational quantum circuits involves embedding the data into a quantum Hilbert space and optimizing the circuit parameters to train the measurement process. In this context, the efficacy of QSL is inherently influenced by the selection of quantum embedding. In this study, we introduce a classical-quantum hybrid approach for optimizing quantum embedding beyond the limitations of the standard circuit model of quantum computation (i.e., completely positive and trace-preserving maps) for general multi-channel data. We benchmark the performance of various models in our framework using the CIFAR-10 and Tiny ImageNet datasets and provide theoretical analyses that guide model design and optimization.
Improving Quantum Machine Learning via Heat-Bath Algorithmic Cooling
Jan 05, 2025



Abstract:This work introduces an approach rooted in quantum thermodynamics to enhance sampling efficiency in quantum machine learning (QML). We propose conceptualizing quantum supervised learning as a thermodynamic cooling process. Building on this concept, we develop a quantum refrigerator protocol that enhances sample efficiency during training and prediction without the need for Grover iterations or quantum phase estimation. Inspired by heat-bath algorithmic cooling protocols, our method alternates entropy compression and thermalization steps to decrease the entropy of qubits, increasing polarization towards the dominant bias. This technique minimizes the computational overhead associated with estimating classification scores and gradients, presenting a practical and efficient solution for QML algorithms compatible with noisy intermediate-scale quantum devices.
Understanding Generalization in Quantum Machine Learning with Margins
Nov 11, 2024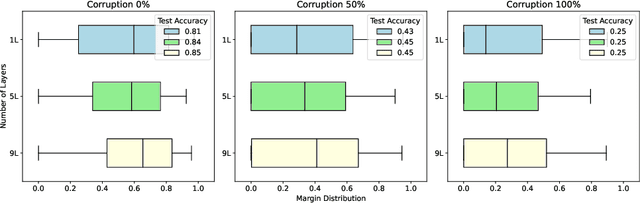
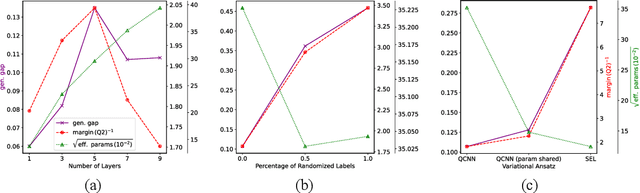
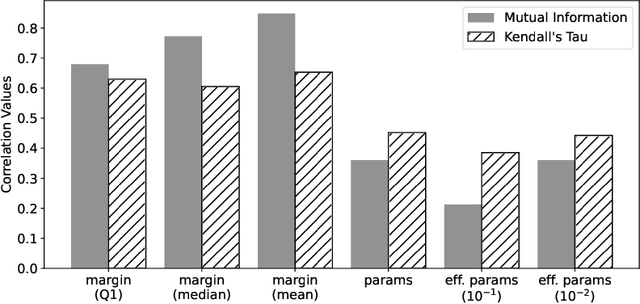
Abstract:Understanding and improving generalization capabilities is crucial for both classical and quantum machine learning (QML). Recent studies have revealed shortcomings in current generalization theories, particularly those relying on uniform bounds, across both classical and quantum settings. In this work, we present a margin-based generalization bound for QML models, providing a more reliable framework for evaluating generalization. Our experimental studies on the quantum phase recognition (QPR) dataset demonstrate that margin-based metrics are strong predictors of generalization performance, outperforming traditional metrics like parameter count. By connecting this margin-based metric to quantum information theory, we demonstrate how to enhance the generalization performance of QML through a classical-quantum hybrid approach when applied to classical data.
Expressivity of deterministic quantum computation with one qubit
Nov 05, 2024Abstract:Deterministic quantum computation with one qubit (DQC1) is of significant theoretical and practical interest due to its computational advantages in certain problems, despite its subuniversality with limited quantum resources. In this work, we introduce parameterized DQC1 as a quantum machine learning model. We demonstrate that the gradient of the measurement outcome of a DQC1 circuit with respect to its gate parameters can be computed directly using the DQC1 protocol. This allows for gradient-based optimization of DQC1 circuits, positioning DQC1 as the sole quantum protocol for both training and inference. We then analyze the expressivity of the parameterized DQC1 circuits, characterizing the set of learnable functions, and show that DQC1-based machine learning (ML) is as powerful as quantum neural networks based on universal computation. Our findings highlight the potential of DQC1 as a practical and versatile platform for ML, capable of rivaling more complex quantum computing models while utilizing simpler quantum resources.
Optimizing Quantum Convolutional Neural Network Architectures for Arbitrary Data Dimension
Mar 28, 2024



Abstract:Quantum convolutional neural networks (QCNNs) represent a promising approach in quantum machine learning, paving new directions for both quantum and classical data analysis. This approach is particularly attractive due to the absence of the barren plateau problem, a fundamental challenge in training quantum neural networks (QNNs), and its feasibility. However, a limitation arises when applying QCNNs to classical data. The network architecture is most natural when the number of input qubits is a power of two, as this number is reduced by a factor of two in each pooling layer. The number of input qubits determines the dimensions (i.e. the number of features) of the input data that can be processed, restricting the applicability of QCNN algorithms to real-world data. To address this issue, we propose a QCNN architecture capable of handling arbitrary input data dimensions while optimizing the allocation of quantum resources such as ancillary qubits and quantum gates. This optimization is not only important for minimizing computational resources, but also essential in noisy intermediate-scale quantum (NISQ) computing, as the size of the quantum circuits that can be executed reliably is limited. Through numerical simulations, we benchmarked the classification performance of various QCNN architectures when handling arbitrary input data dimensions on the MNIST and Breast Cancer datasets. The results validate that the proposed QCNN architecture achieves excellent classification performance while utilizing a minimal resource overhead, providing an optimal solution when reliable quantum computation is constrained by noise and imperfections.
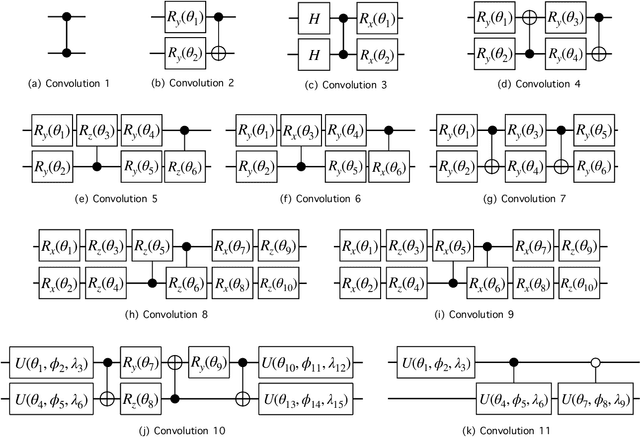
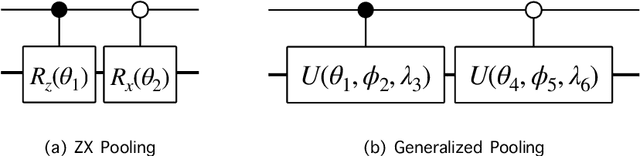
Architecture representations for quantum convolutional neural networks
Oct 26, 2022Abstract:The Quantum Convolutional Neural Network (QCNN) is a quantum circuit model inspired by the architecture of Convolutional Neural Networks (CNNs). The success of CNNs is largely due to its ability to learn high level features from raw data rather than requiring manual feature design. Neural Architecture Search (NAS) continues this trend by learning network architecture, alleviating the need for its manual construction and have been able to generate state of the art models automatically. Search space design is a crucial step in NAS and there is currently no formal framework through which it can be achieved for QCNNs. In this work we provide such a framework by utilizing techniques from NAS to create an architectural representation for QCNNs that facilitate search space design and automatic model generation. This is done by specifying primitive operations, such as convolutions and pooling, in such a way that they can be dynamically stacked on top of each other to form different architectures. This way, QCNN search spaces can be created by controlling the sequence and hyperparameters of stacked primitives, allowing the capture of different design motifs. We show this by generating QCNNs that belong to a popular family of parametric quantum circuits, those resembling reverse binary trees. We then benchmark this family of models on a music genre classification dataset, GTZAN. Showing that alternating architecture impact model performance more than other modelling components such as choice of unitary ansatz and data encoding, resulting in a way to improve model performance without increasing its complexity. Finally we provide an open source python package that enable dynamic QCNN creation by system or hand, based off the work presented in this paper, facilitating search space design.
Classical-to-quantum convolutional neural network transfer learning
Aug 31, 2022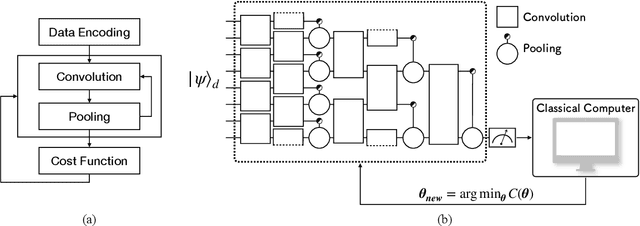
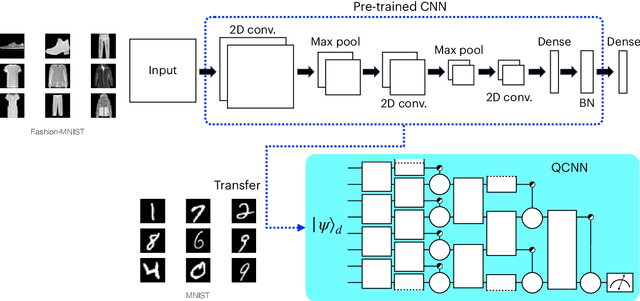
Abstract:Machine learning using quantum convolutional neural networks (QCNNs) has demonstrated success in both quantum and classical data classification. In previous studies, QCNNs attained a higher classification accuracy than their classical counterparts under the same training conditions in the few-parameter regime. However, the general performance of large-scale quantum models is difficult to examine because of the limited size of quantum circuits, which can be reliably implemented in the near future. We propose transfer learning as an effective strategy for utilizing small QCNNs in the noisy intermediate-scale quantum era to the full extent. In the classical-to-quantum transfer learning framework, a QCNN can solve complex classification problems without requiring a large-scale quantum circuit by utilizing a pre-trained classical convolutional neural network (CNN). We perform numerical simulations of QCNN models with various sets of quantum convolution and pooling operations for MNIST data classification under transfer learning, in which a classical CNN is trained with Fashion-MNIST data. The results show that transfer learning from classical to quantum CNN performs considerably better than purely classical transfer learning models under similar training conditions.
Variational Quantum Approximate Support Vector Machine With Inference Transfer
Jun 29, 2022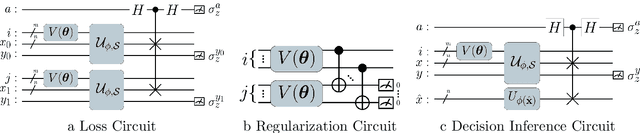
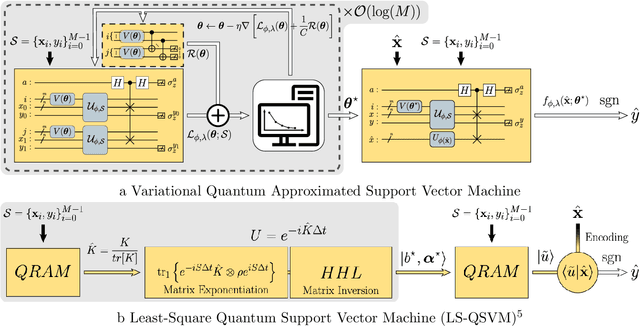
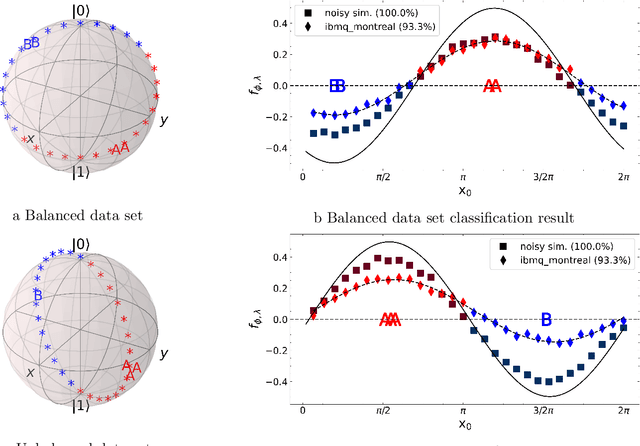
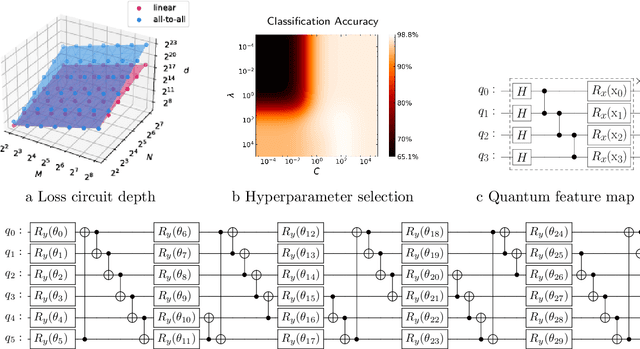
Abstract:A kernel-based quantum classifier is the most interesting and powerful quantum machine learning technique for hyperlinear classification of complex data, which can be easily realized in shallow-depth quantum circuits such as a SWAP test classifier. Surprisingly, a support vector machine can be realized inherently and explicitly on these circuits by introduction of a variational scheme to map the quadratic optimization problem of the SVM theory to a quantum-classical variational optimization problem. This scheme is realized with parameterized quantum circuits (PQC) to create a nonuniform weight vector to index qubits that can evaluate training loss and classification score in a linear time. We train the classical parameters of this Variational Quantum Approximate Support Vector Machine (VQASVM), which can be transferred to many copies of other VQASVM decision inference circuits for classification of new query data. Our VQASVM algorithm is experimented with toy example data sets on cloud-based quantum machines for feasibility evaluation, and numerically investigated to evaluate its performance on a standard iris flower data set. The accuracy of iris data classification reached 98.8%.
A divide-and-conquer algorithm for quantum state preparation
Aug 04, 2020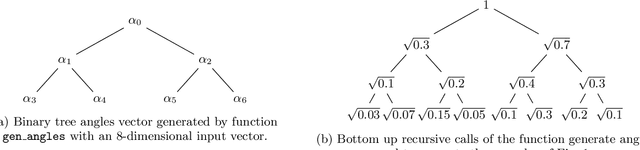
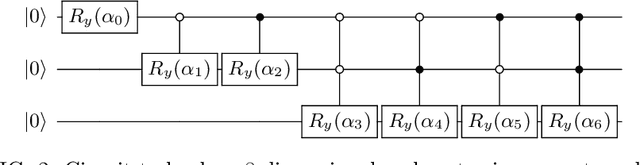
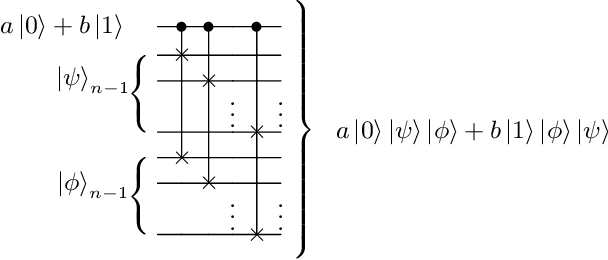
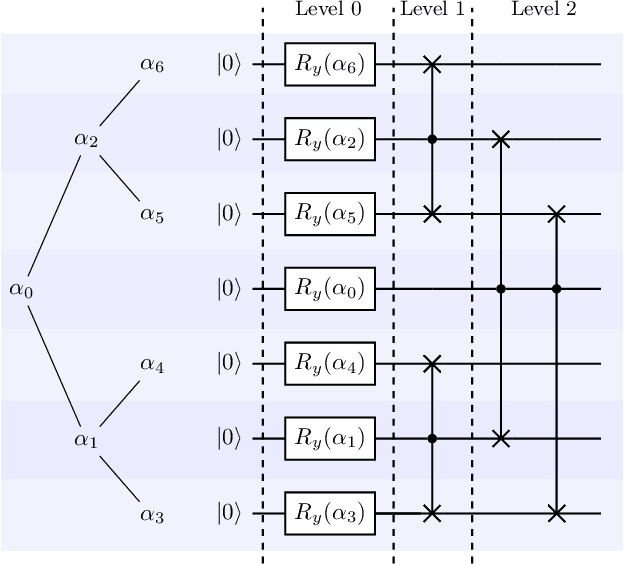
Abstract:Advantages in several fields of research and industry are expected with the rise of quantum computers. However, the computational cost to load classical data in quantum computers can impose restrictions on possible quantum speedups. Known algorithms to create arbitrary quantum states require quantum circuits with depth O(N) to load an N-dimensional vector. Here, we show that it is possible to load an N-dimensional vector with a quantum circuit with polylogarithmic depth and entangled information in ancillary qubits. Results show that we can efficiently load data in quantum devices using a divide-and-conquer strategy to exchange computational time for space. We demonstrate a proof of concept on a real quantum device and present two applications for quantum machine learning. We expect that this new loading strategy allows the quantum speedup of tasks that require to load a significant volume of information to quantum devices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge