Optimizing Quantum Convolutional Neural Network Architectures for Arbitrary Data Dimension

Quantum convolutional neural networks (QCNNs) represent a promising approach in quantum machine learning, paving new directions for both quantum and classical data analysis. This approach is particularly attractive due to the absence of the barren plateau problem, a fundamental challenge in training quantum neural networks (QNNs), and its feasibility. However, a limitation arises when applying QCNNs to classical data. The network architecture is most natural when the number of input qubits is a power of two, as this number is reduced by a factor of two in each pooling layer. The number of input qubits determines the dimensions (i.e. the number of features) of the input data that can be processed, restricting the applicability of QCNN algorithms to real-world data. To address this issue, we propose a QCNN architecture capable of handling arbitrary input data dimensions while optimizing the allocation of quantum resources such as ancillary qubits and quantum gates. This optimization is not only important for minimizing computational resources, but also essential in noisy intermediate-scale quantum (NISQ) computing, as the size of the quantum circuits that can be executed reliably is limited. Through numerical simulations, we benchmarked the classification performance of various QCNN architectures when handling arbitrary input data dimensions on the MNIST and Breast Cancer datasets. The results validate that the proposed QCNN architecture achieves excellent classification performance while utilizing a minimal resource overhead, providing an optimal solution when reliable quantum computation is constrained by noise and imperfections.

Variational Quantum Approximate Support Vector Machine With Inference Transfer

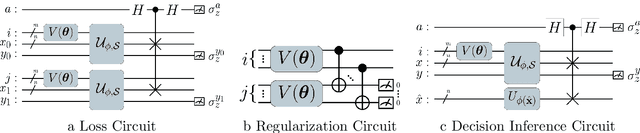
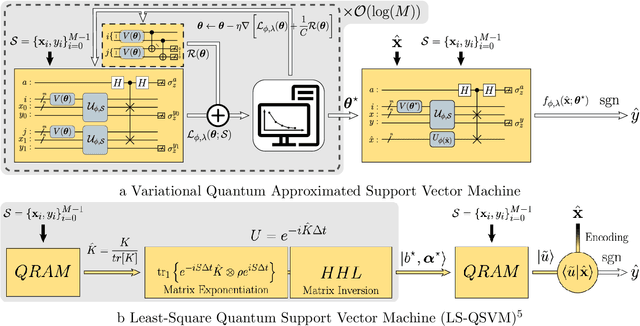
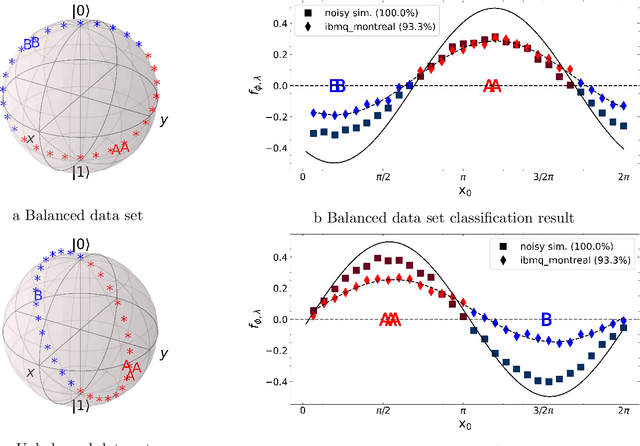
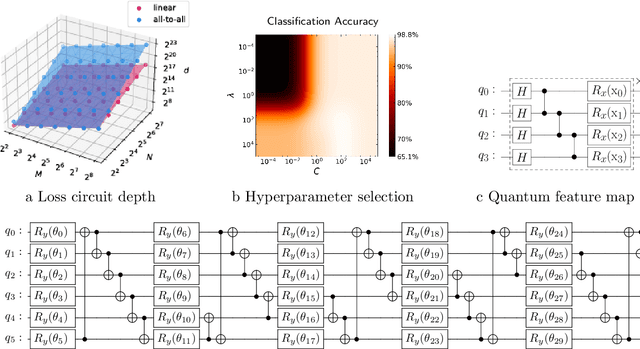
A kernel-based quantum classifier is the most interesting and powerful quantum machine learning technique for hyperlinear classification of complex data, which can be easily realized in shallow-depth quantum circuits such as a SWAP test classifier. Surprisingly, a support vector machine can be realized inherently and explicitly on these circuits by introduction of a variational scheme to map the quadratic optimization problem of the SVM theory to a quantum-classical variational optimization problem. This scheme is realized with parameterized quantum circuits (PQC) to create a nonuniform weight vector to index qubits that can evaluate training loss and classification score in a linear time. We train the classical parameters of this Variational Quantum Approximate Support Vector Machine (VQASVM), which can be transferred to many copies of other VQASVM decision inference circuits for classification of new query data. Our VQASVM algorithm is experimented with toy example data sets on cloud-based quantum machines for feasibility evaluation, and numerically investigated to evaluate its performance on a standard iris flower data set. The accuracy of iris data classification reached 98.8%.