Optimizing Quantum Convolutional Neural Network Architectures for Arbitrary Data Dimension

Quantum convolutional neural networks (QCNNs) represent a promising approach in quantum machine learning, paving new directions for both quantum and classical data analysis. This approach is particularly attractive due to the absence of the barren plateau problem, a fundamental challenge in training quantum neural networks (QNNs), and its feasibility. However, a limitation arises when applying QCNNs to classical data. The network architecture is most natural when the number of input qubits is a power of two, as this number is reduced by a factor of two in each pooling layer. The number of input qubits determines the dimensions (i.e. the number of features) of the input data that can be processed, restricting the applicability of QCNN algorithms to real-world data. To address this issue, we propose a QCNN architecture capable of handling arbitrary input data dimensions while optimizing the allocation of quantum resources such as ancillary qubits and quantum gates. This optimization is not only important for minimizing computational resources, but also essential in noisy intermediate-scale quantum (NISQ) computing, as the size of the quantum circuits that can be executed reliably is limited. Through numerical simulations, we benchmarked the classification performance of various QCNN architectures when handling arbitrary input data dimensions on the MNIST and Breast Cancer datasets. The results validate that the proposed QCNN architecture achieves excellent classification performance while utilizing a minimal resource overhead, providing an optimal solution when reliable quantum computation is constrained by noise and imperfections.

Quantum Neural Architecture Search with Quantum Circuits Metric and Bayesian Optimization

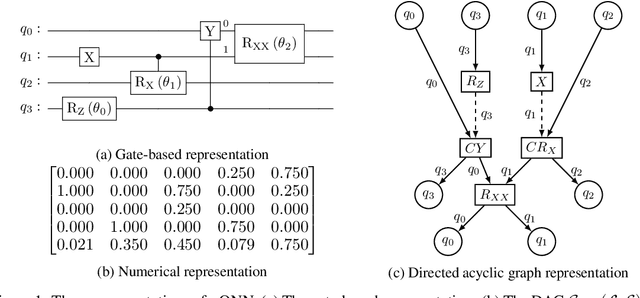
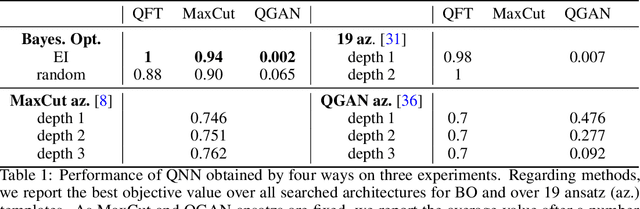
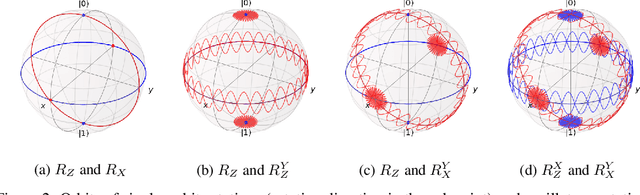
Quantum neural networks are promising for a wide range of applications in the Noisy Intermediate-Scale Quantum era. As such, there is an increasing demand for automatic quantum neural architecture search. We tackle this challenge by designing a quantum circuits metric for Bayesian optimization with Gaussian process. To this goal, we propose a new quantum gates distance that characterizes the gates' action over every quantum state and provide a theoretical perspective on its geometrical properties. Our approach significantly outperforms the benchmark on three empirical quantum machine learning problems including training a quantum generative adversarial network, solving combinatorial optimization in the MaxCut problem, and simulating quantum Fourier transform. Our method can be extended to characterize behaviors of various quantum machine learning models.