Provably faster randomized and quantum algorithms for k-means clustering via uniform sampling

The $k$-means algorithm (Lloyd's algorithm) is a widely used method for clustering unlabeled data. A key bottleneck of the $k$-means algorithm is that each iteration requires time linear in the number of data points, which can be expensive in big data applications. This was improved in recent works proposing quantum and quantum-inspired classical algorithms to approximate the $k$-means algorithm locally, in time depending only logarithmically on the number of data points (along with data dependent parameters) [$q$-means: A quantum algorithm for unsupervised machine learning; Kerenidis, Landman, Luongo, and Prakash, NeurIPS 2019; Do you know what $q$-means?, Doriguello, Luongo, Tang]. In this work, we describe a simple randomized mini-batch $k$-means algorithm and a quantum algorithm inspired by the classical algorithm. We prove worse-case guarantees that significantly improve upon the bounds for previous algorithms. Our improvements are due to a careful use of uniform sampling, which preserves certain symmetries of the $k$-means problem that are not preserved in previous algorithms that use data norm-based sampling.

Cross-Problem Parameter Transfer in Quantum Approximate Optimization Algorithm: A Machine Learning Approach

Quantum Approximate Optimization Algorithm (QAOA) is one of the most promising candidates to achieve the quantum advantage in solving combinatorial optimization problems. The process of finding a good set of variational parameters in the QAOA circuit has proven to be challenging due to multiple factors, such as barren plateaus. As a result, there is growing interest in exploiting parameter transferability, where parameter sets optimized for one problem instance are transferred to another that could be more complex either to estimate the solution or to serve as a warm start for further optimization. But can we transfer parameters from one class of problems to another? Leveraging parameter sets learned from a well-studied class of problems could help navigate the less studied one, reducing optimization overhead and mitigating performance pitfalls. In this paper, we study whether pretrained QAOA parameters of MaxCut can be used as is or to warm start the Maximum Independent Set (MIS) circuits. Specifically, we design machine learning models to find good donor candidates optimized on MaxCut and apply their parameters to MIS acceptors. Our experimental results show that such parameter transfer can significantly reduce the number of optimization iterations required while achieving comparable approximation ratios.

QAdaPrune: Adaptive Parameter Pruning For Training Variational Quantum Circuits

In the present noisy intermediate scale quantum computing era, there is a critical need to devise methods for the efficient implementation of gate-based variational quantum circuits. This ensures that a range of proposed applications can be deployed on real quantum hardware. The efficiency of quantum circuit is desired both in the number of trainable gates and the depth of the overall circuit. The major concern of barren plateaus has made this need for efficiency even more acute. The problem of efficient quantum circuit realization has been extensively studied in the literature to reduce gate complexity and circuit depth. Another important approach is to design a method to reduce the \emph{parameter complexity} in a variational quantum circuit. Existing methods include hyperparameter-based parameter pruning which introduces an additional challenge of finding the best hyperparameters for different applications. In this paper, we present \emph{QAdaPrune} - an adaptive parameter pruning algorithm that automatically determines the threshold and then intelligently prunes the redundant and non-performing parameters. We show that the resulting sparse parameter sets yield quantum circuits that perform comparably to the unpruned quantum circuits and in some cases may enhance trainability of the circuits even if the original quantum circuit gets stuck in a barren plateau.\\ \noindent{\bf Reproducibility}: The source code and data are available at \url{https://github.com/aicaffeinelife/QAdaPrune.git}

Quantum Neural Architecture Search with Quantum Circuits Metric and Bayesian Optimization

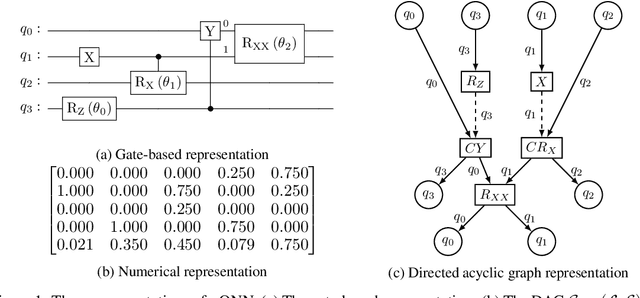
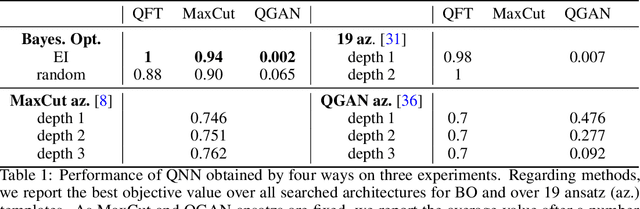
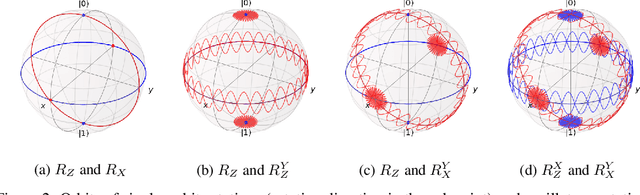
Quantum neural networks are promising for a wide range of applications in the Noisy Intermediate-Scale Quantum era. As such, there is an increasing demand for automatic quantum neural architecture search. We tackle this challenge by designing a quantum circuits metric for Bayesian optimization with Gaussian process. To this goal, we propose a new quantum gates distance that characterizes the gates' action over every quantum state and provide a theoretical perspective on its geometrical properties. Our approach significantly outperforms the benchmark on three empirical quantum machine learning problems including training a quantum generative adversarial network, solving combinatorial optimization in the MaxCut problem, and simulating quantum Fourier transform. Our method can be extended to characterize behaviors of various quantum machine learning models.