Quantum Neural Architecture Search with Quantum Circuits Metric and Bayesian Optimization
Paper and Code
Jun 28, 2022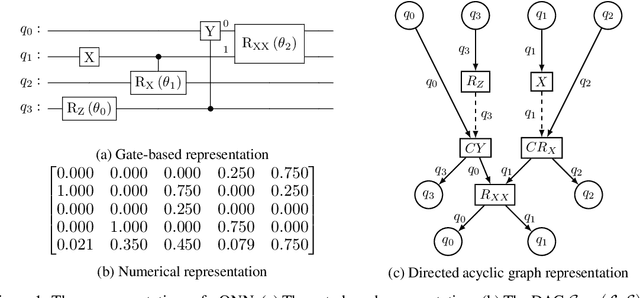
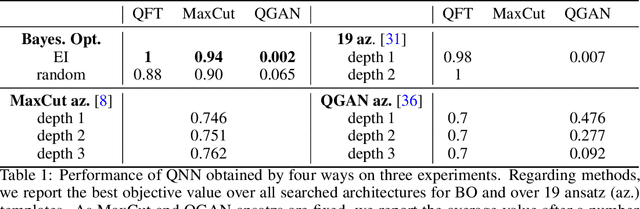
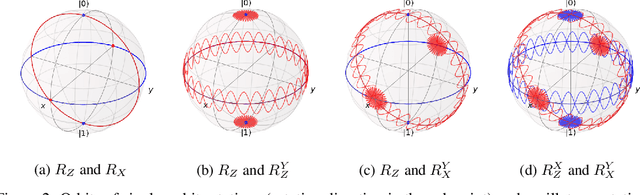

Quantum neural networks are promising for a wide range of applications in the Noisy Intermediate-Scale Quantum era. As such, there is an increasing demand for automatic quantum neural architecture search. We tackle this challenge by designing a quantum circuits metric for Bayesian optimization with Gaussian process. To this goal, we propose a new quantum gates distance that characterizes the gates' action over every quantum state and provide a theoretical perspective on its geometrical properties. Our approach significantly outperforms the benchmark on three empirical quantum machine learning problems including training a quantum generative adversarial network, solving combinatorial optimization in the MaxCut problem, and simulating quantum Fourier transform. Our method can be extended to characterize behaviors of various quantum machine learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge