Optimizing Quantum Convolutional Neural Network Architectures for Arbitrary Data Dimension

Quantum convolutional neural networks (QCNNs) represent a promising approach in quantum machine learning, paving new directions for both quantum and classical data analysis. This approach is particularly attractive due to the absence of the barren plateau problem, a fundamental challenge in training quantum neural networks (QNNs), and its feasibility. However, a limitation arises when applying QCNNs to classical data. The network architecture is most natural when the number of input qubits is a power of two, as this number is reduced by a factor of two in each pooling layer. The number of input qubits determines the dimensions (i.e. the number of features) of the input data that can be processed, restricting the applicability of QCNN algorithms to real-world data. To address this issue, we propose a QCNN architecture capable of handling arbitrary input data dimensions while optimizing the allocation of quantum resources such as ancillary qubits and quantum gates. This optimization is not only important for minimizing computational resources, but also essential in noisy intermediate-scale quantum (NISQ) computing, as the size of the quantum circuits that can be executed reliably is limited. Through numerical simulations, we benchmarked the classification performance of various QCNN architectures when handling arbitrary input data dimensions on the MNIST and Breast Cancer datasets. The results validate that the proposed QCNN architecture achieves excellent classification performance while utilizing a minimal resource overhead, providing an optimal solution when reliable quantum computation is constrained by noise and imperfections.

A divide-and-conquer algorithm for quantum state preparation

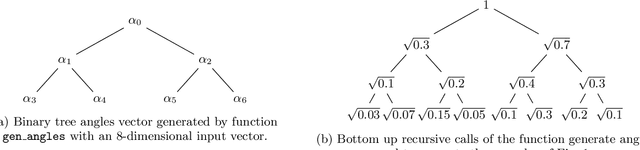
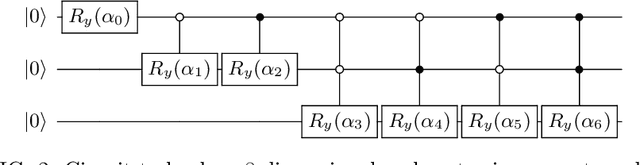
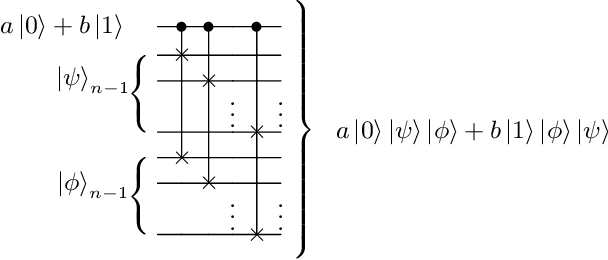
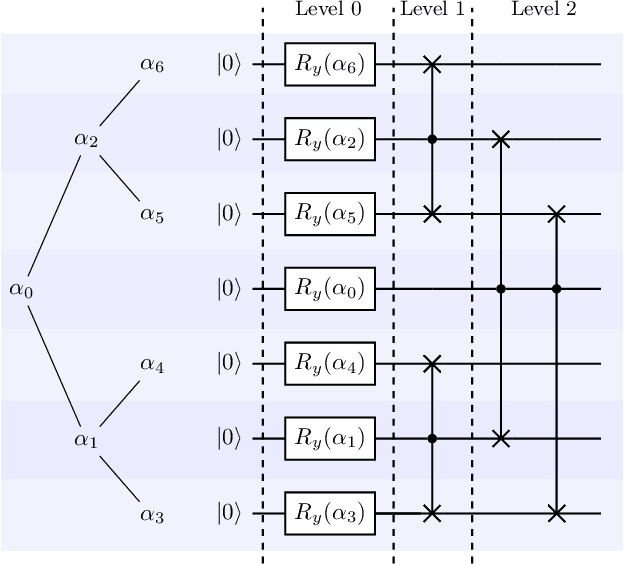
Advantages in several fields of research and industry are expected with the rise of quantum computers. However, the computational cost to load classical data in quantum computers can impose restrictions on possible quantum speedups. Known algorithms to create arbitrary quantum states require quantum circuits with depth O(N) to load an N-dimensional vector. Here, we show that it is possible to load an N-dimensional vector with a quantum circuit with polylogarithmic depth and entangled information in ancillary qubits. Results show that we can efficiently load data in quantum devices using a divide-and-conquer strategy to exchange computational time for space. We demonstrate a proof of concept on a real quantum device and present two applications for quantum machine learning. We expect that this new loading strategy allows the quantum speedup of tasks that require to load a significant volume of information to quantum devices.