Scalable Neural Decoders for Practical Real-Time Quantum Error Correction

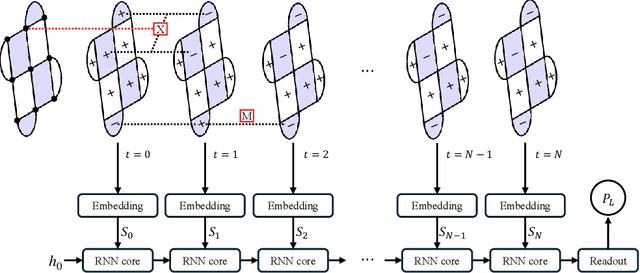
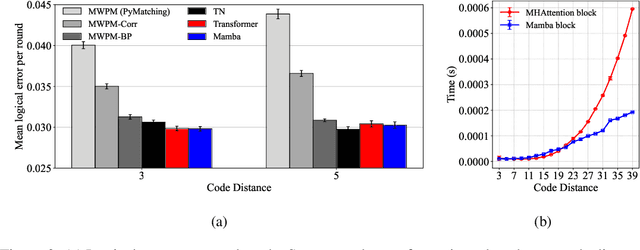
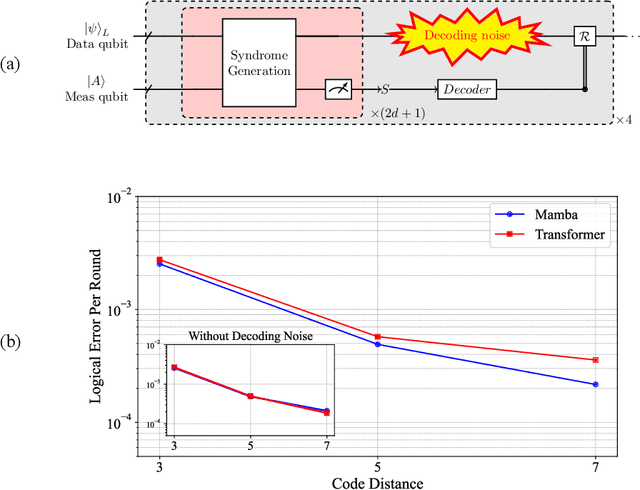
Real-time, scalable, and accurate decoding is a critical component for realizing a fault-tolerant quantum computer. While Transformer-based neural decoders such as \textit{AlphaQubit} have demonstrated high accuracy, the computational complexity of their core attention mechanism, which scales as $\mathcal{O}(d^4)$ with code distance $d$, results in decoding speeds insufficient for practical real-time applications. In this work, we introduce and evaluate a \textit{Mamba}-based decoder, a state-space model with $\mathcal{O}(d^2)$ complexity. In memory experiments using Sycamore hardware data, our Mamba decoder matches the performance of its Transformer-based counterpart, providing that its superior efficiency does not come at the cost of performance. Crucially, in simulated real-time scenarios that account for decoder-induced noise, the Mamba decoder significantly outperforms the Transformer, exhibiting a higher error threshold of $0.0104$ compared to $0.0097$. These results demonstrate that Mamba decoders offer a compelling balance between speed and accuracy, making them a promising architecture for scalable, real-time quantum error correction.

Multi-channel convolutional neural quantum embedding

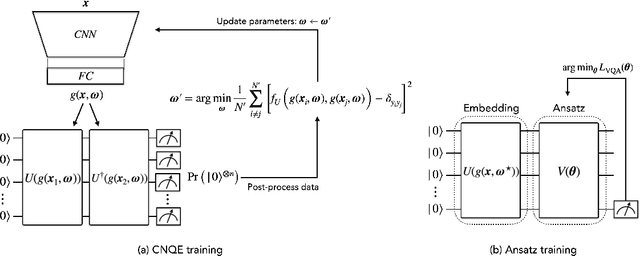
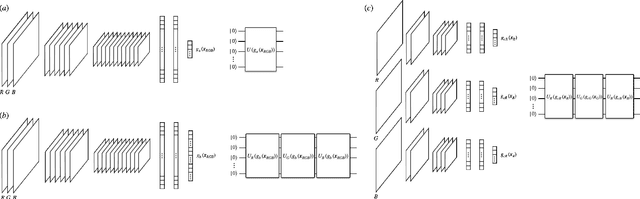
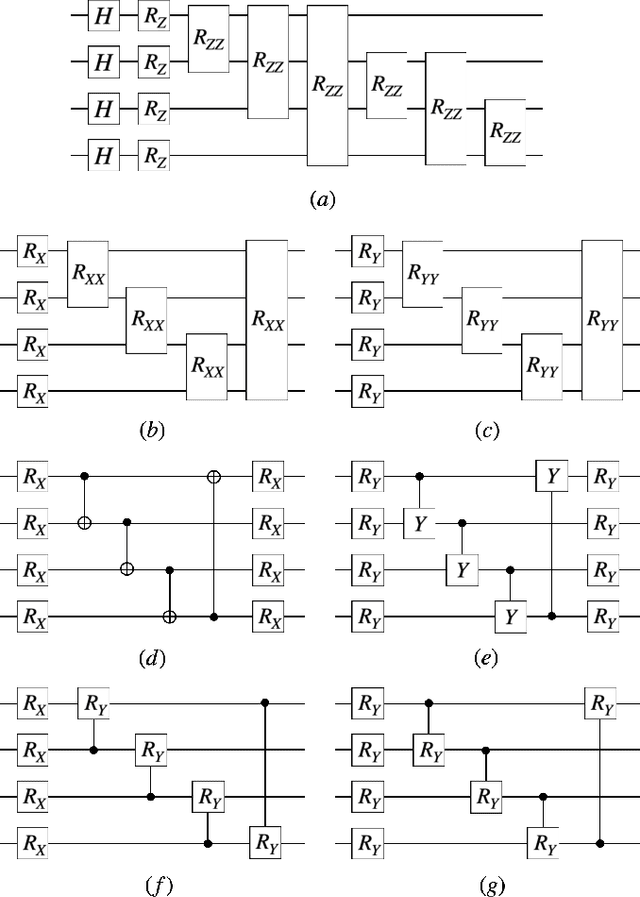
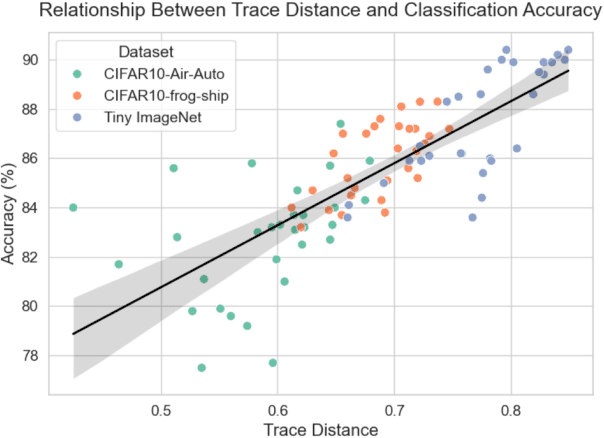
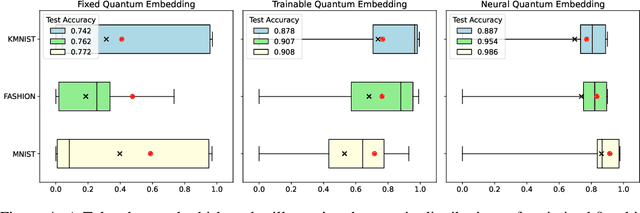
Classification using variational quantum circuits is a promising frontier in quantum machine learning. Quantum supervised learning (QSL) applied to classical data using variational quantum circuits involves embedding the data into a quantum Hilbert space and optimizing the circuit parameters to train the measurement process. In this context, the efficacy of QSL is inherently influenced by the selection of quantum embedding. In this study, we introduce a classical-quantum hybrid approach for optimizing quantum embedding beyond the limitations of the standard circuit model of quantum computation (i.e., completely positive and trace-preserving maps) for general multi-channel data. We benchmark the performance of various models in our framework using the CIFAR-10 and Tiny ImageNet datasets and provide theoretical analyses that guide model design and optimization.

Understanding Generalization in Quantum Machine Learning with Margins

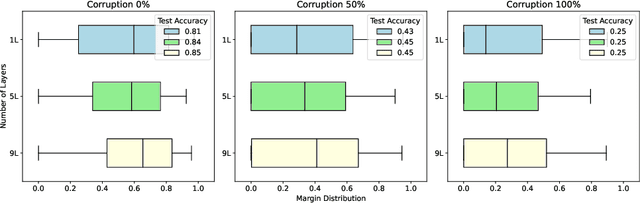
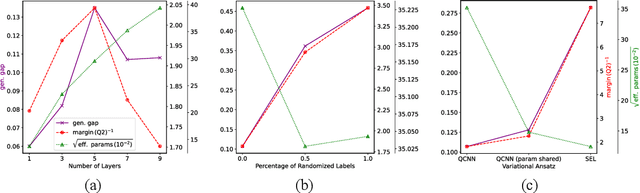
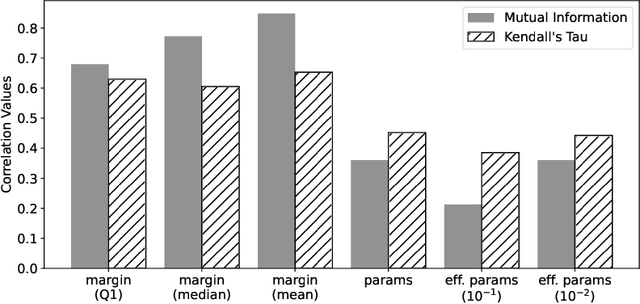
Understanding and improving generalization capabilities is crucial for both classical and quantum machine learning (QML). Recent studies have revealed shortcomings in current generalization theories, particularly those relying on uniform bounds, across both classical and quantum settings. In this work, we present a margin-based generalization bound for QML models, providing a more reliable framework for evaluating generalization. Our experimental studies on the quantum phase recognition (QPR) dataset demonstrate that margin-based metrics are strong predictors of generalization performance, outperforming traditional metrics like parameter count. By connecting this margin-based metric to quantum information theory, we demonstrate how to enhance the generalization performance of QML through a classical-quantum hybrid approach when applied to classical data.