Transfer learning in hybrid classical-quantum neural networks

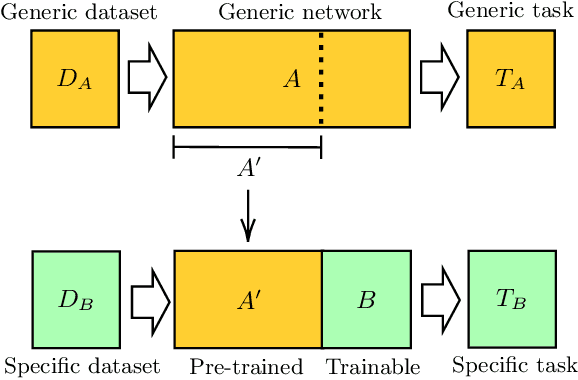
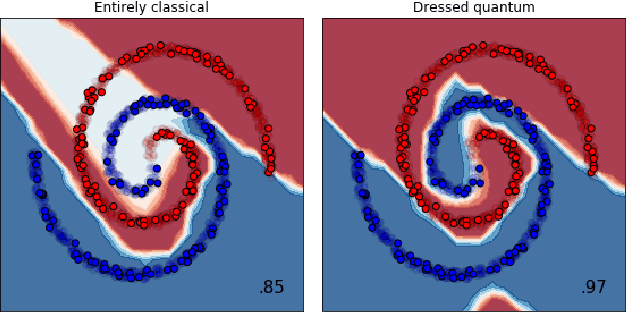
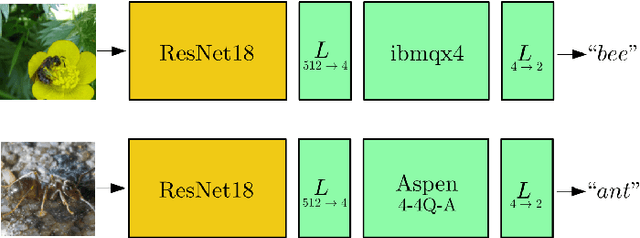
We extend the concept of transfer learning, widely applied in modern machine learning algorithms, to the emerging context of hybrid neural networks composed of classical and quantum elements. We propose different implementations of hybrid transfer learning, but we focus mainly on the paradigm in which a pre-trained classical network is modified and augmented by a final variational quantum circuit. This approach is particularly attractive in the current era of intermediate-scale quantum technology since it allows to optimally pre-process high dimensional data (e.g., images) with any state-of-the-art classical network and to embed a select set of highly informative features into a quantum processor. We present several proof-of-concept examples of the convenient application of quantum transfer learning for image recognition and quantum state classification. We use the cross-platform software library PennyLane to experimentally test a high-resolution image classifier with two different quantum computers, respectively provided by IBM and Rigetti.

Continuous-variable quantum neural networks

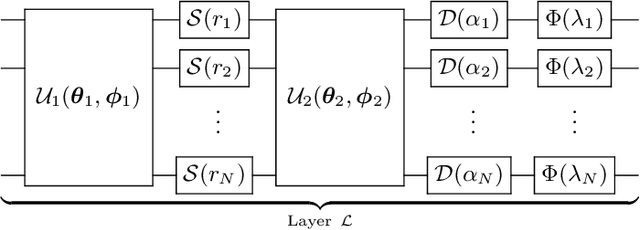
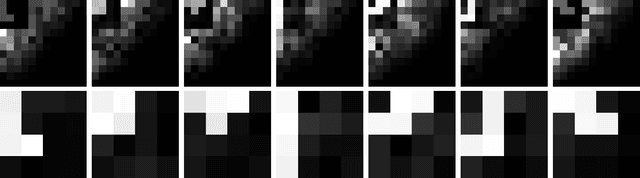
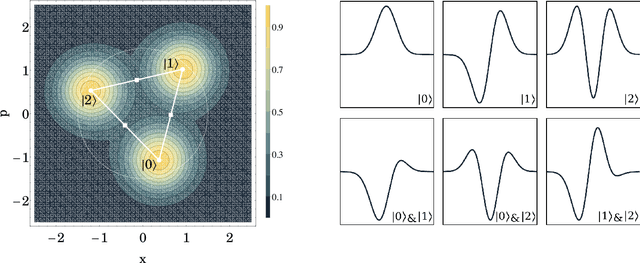
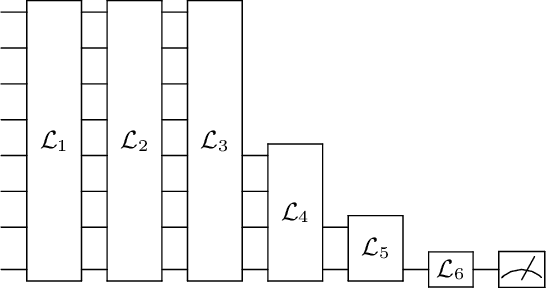
We introduce a general method for building neural networks on quantum computers. The quantum neural network is a variational quantum circuit built in the continuous-variable (CV) architecture, which encodes quantum information in continuous degrees of freedom such as the amplitudes of the electromagnetic field. This circuit contains a layered structure of continuously parameterized gates which is universal for CV quantum computation. Affine transformations and nonlinear activation functions, two key elements in neural networks, are enacted in the quantum network using Gaussian and non-Gaussian gates, respectively. The non-Gaussian gates provide both the nonlinearity and the universality of the model. Due to the structure of the CV model, the CV quantum neural network can encode highly nonlinear transformations while remaining completely unitary. We show how a classical network can be embedded into the quantum formalism and propose quantum versions of various specialized model such as convolutional, recurrent, and residual networks. Finally, we present numerous modeling experiments built with the Strawberry Fields software library. These experiments, including a classifier for fraud detection, a network which generates Tetris images, and a hybrid classical-quantum autoencoder, demonstrate the capability and adaptability of CV quantum neural networks.