Learning Unitaries by Gradient Descent
Paper and Code
Feb 18, 2020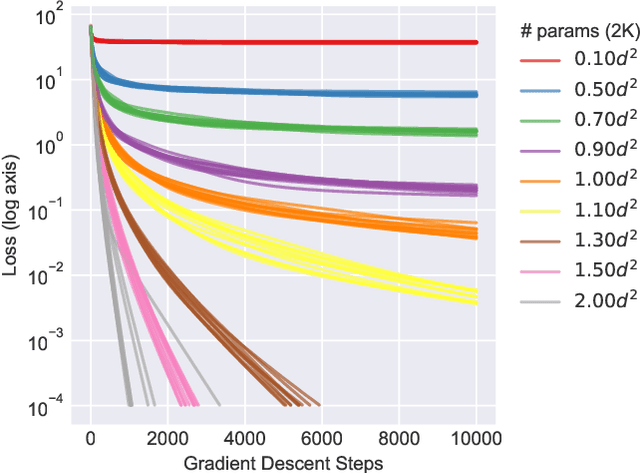
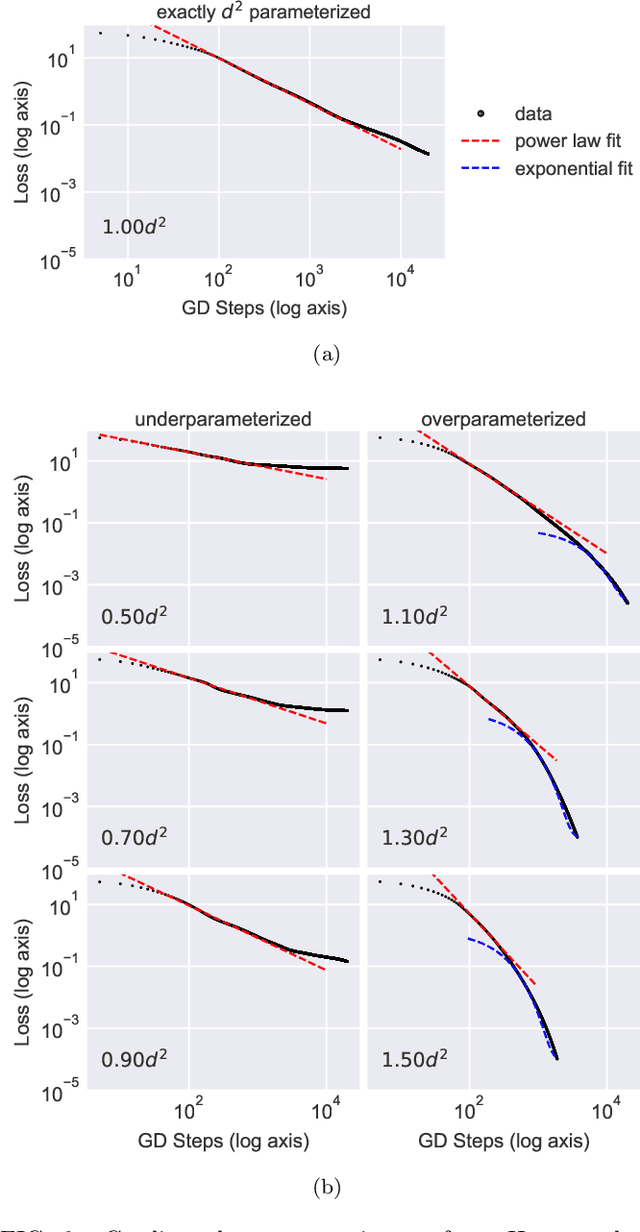


We study the hardness of learning unitary transformations in $U(d)$ via gradient descent on time parameters of alternating operator sequences. We provide numerical evidence that, despite the non-convex nature of the loss landscape, gradient descent always converges to the target unitary when the sequence contains $d^2$ or more parameters. Rates of convergence indicate a "computational phase transition." With less than $d^2$ parameters, gradient descent converges to a sub-optimal solution, whereas with more than $d^2$ parameters, gradient descent converges exponentially to an optimal solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge