Quantum Earth Mover's Distance: A New Approach to Learning Quantum Data

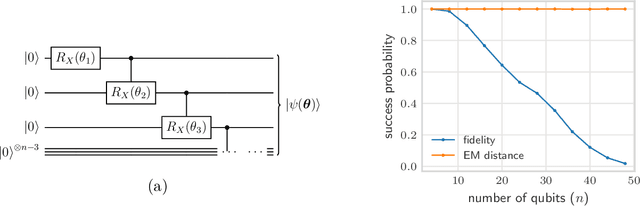
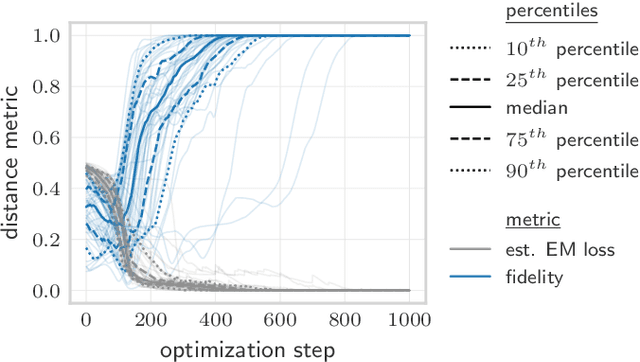
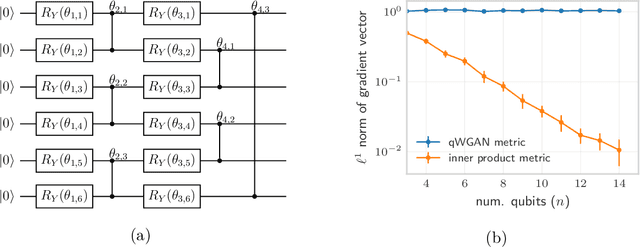
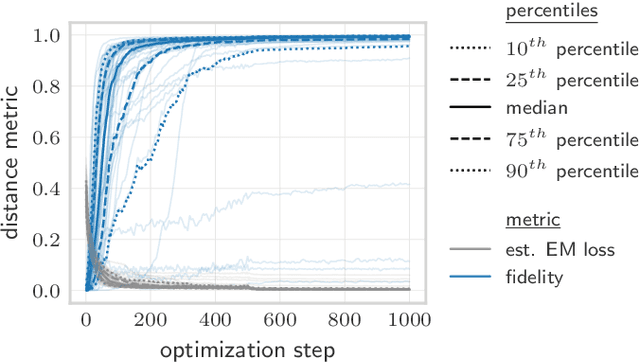
Quantifying how far the output of a learning algorithm is from its target is an essential task in machine learning. However, in quantum settings, the loss landscapes of commonly used distance metrics often produce undesirable outcomes such as poor local minima and exponentially decaying gradients. As a new approach, we consider here the quantum earth mover's (EM) or Wasserstein-1 distance, recently proposed in [De Palma et al., arXiv:2009.04469] as a quantum analog to the classical EM distance. We show that the quantum EM distance possesses unique properties, not found in other commonly used quantum distance metrics, that make quantum learning more stable and efficient. We propose a quantum Wasserstein generative adversarial network (qWGAN) which takes advantage of the quantum EM distance and provides an efficient means of performing learning on quantum data. Our qWGAN requires resources polynomial in the number of qubits, and our numerical experiments demonstrate that it is capable of learning a diverse set of quantum data.

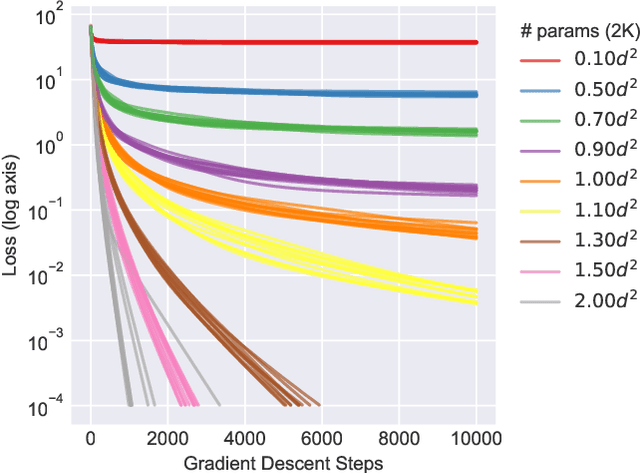
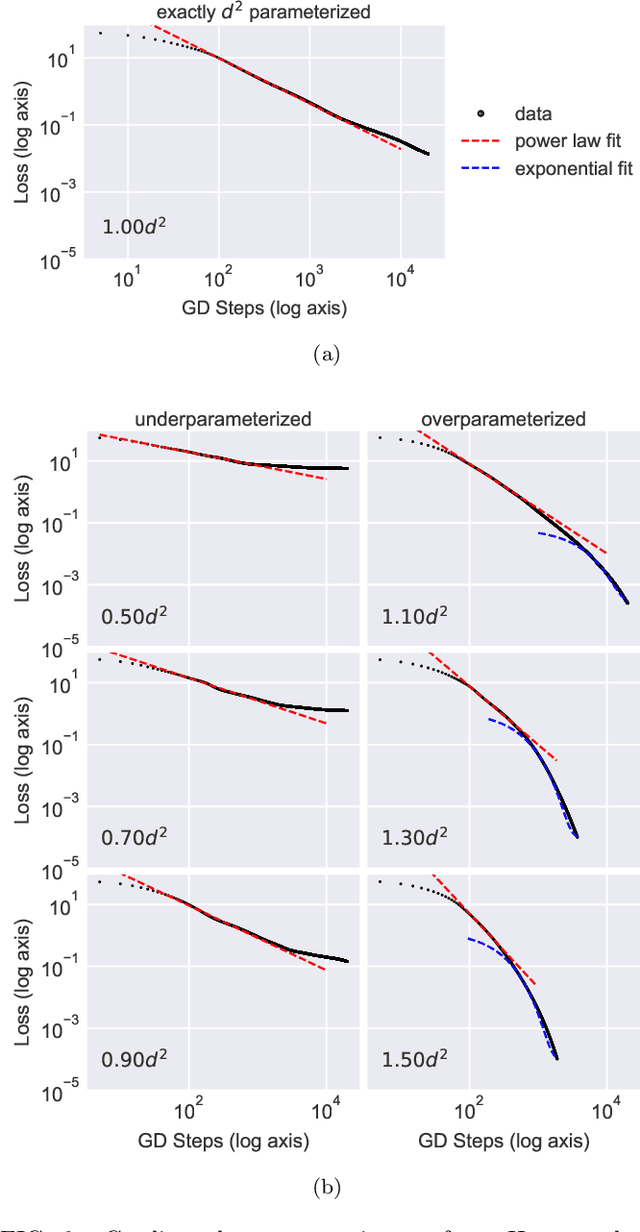
Learning Unitaries by Gradient Descent

We study the hardness of learning unitary transformations in $U(d)$ via gradient descent on time parameters of alternating operator sequences. We provide numerical evidence that, despite the non-convex nature of the loss landscape, gradient descent always converges to the target unitary when the sequence contains $d^2$ or more parameters. Rates of convergence indicate a "computational phase transition." With less than $d^2$ parameters, gradient descent converges to a sub-optimal solution, whereas with more than $d^2$ parameters, gradient descent converges exponentially to an optimal solution.

Deep neural networks are biased towards simple functions

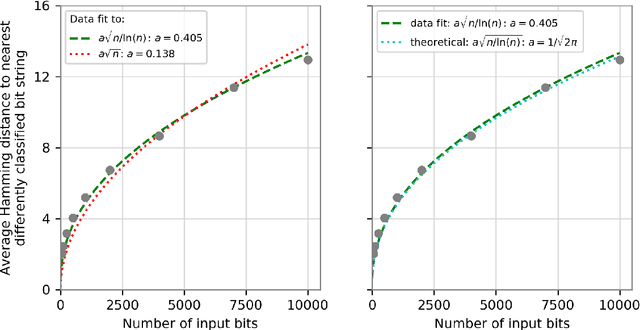
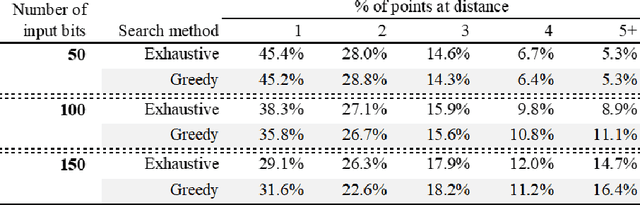
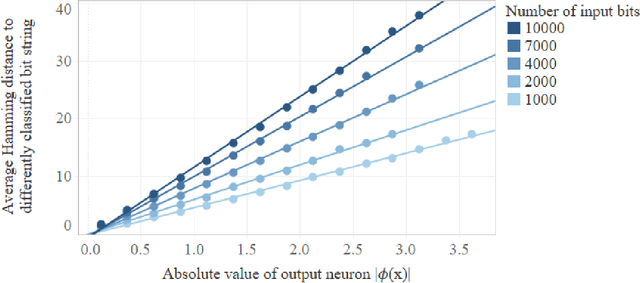
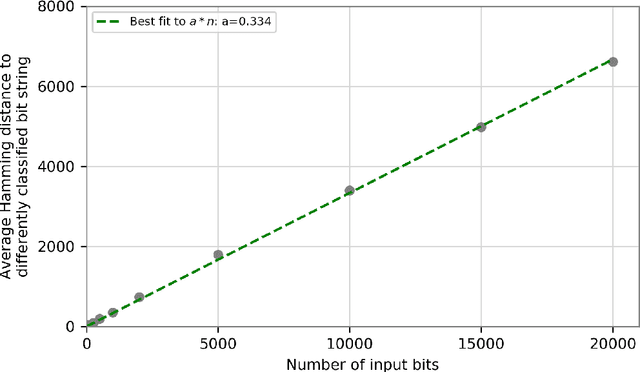
We prove that the binary classifiers of bit strings generated by random wide deep neural networks are biased towards simple functions. The simplicity is captured by the following two properties. For any given input bit string, the average Hamming distance of the closest input bit string with a different classification is at least $\sqrt{n\left/\left(2\pi\ln n\right)\right.}$, where $n$ is the length of the string. Moreover, if the bits of the initial string are flipped randomly, the average number of flips required to change the classification grows linearly with $n$. On the contrary, for a uniformly random binary classifier, the average Hamming distance of the closest input bit string with a different classification is one, and the average number of random flips required to change the classification is two. These results are confirmed by numerical experiments on deep neural networks with two hidden layers, and settle the conjecture stating that random deep neural networks are biased towards simple functions. The conjecture that random deep neural networks are biased towards simple functions was proposed and numerically explored in [Valle P\'erez et al., arXiv:1805.08522] to explain the unreasonably good generalization properties of deep learning algorithms. By providing a precise characterization of the form of this bias towards simplicity, our results open the way to a rigorous proof of the generalization properties of deep learning algorithms in real-world scenarios.