Deep neural networks are biased towards simple functions

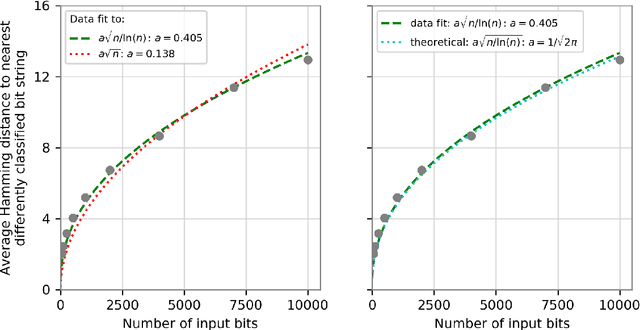
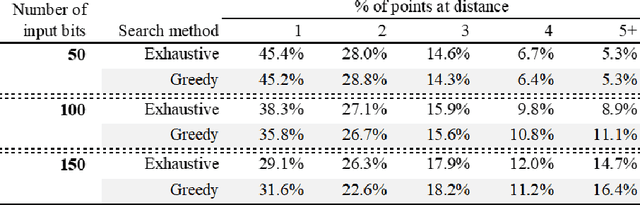
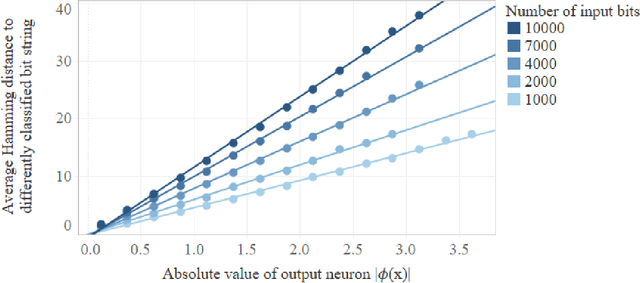
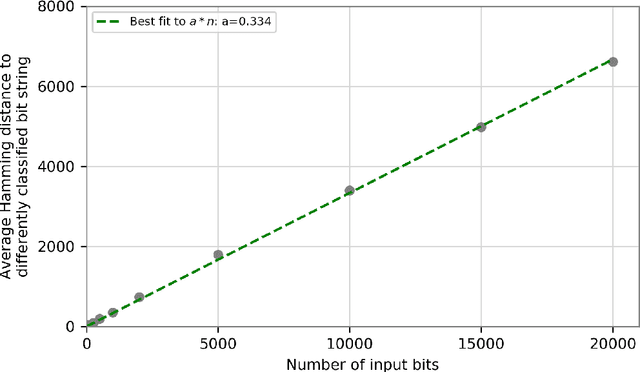
We prove that the binary classifiers of bit strings generated by random wide deep neural networks are biased towards simple functions. The simplicity is captured by the following two properties. For any given input bit string, the average Hamming distance of the closest input bit string with a different classification is at least $\sqrt{n\left/\left(2\pi\ln n\right)\right.}$, where $n$ is the length of the string. Moreover, if the bits of the initial string are flipped randomly, the average number of flips required to change the classification grows linearly with $n$. On the contrary, for a uniformly random binary classifier, the average Hamming distance of the closest input bit string with a different classification is one, and the average number of random flips required to change the classification is two. These results are confirmed by numerical experiments on deep neural networks with two hidden layers, and settle the conjecture stating that random deep neural networks are biased towards simple functions. The conjecture that random deep neural networks are biased towards simple functions was proposed and numerically explored in [Valle P\'erez et al., arXiv:1805.08522] to explain the unreasonably good generalization properties of deep learning algorithms. By providing a precise characterization of the form of this bias towards simplicity, our results open the way to a rigorous proof of the generalization properties of deep learning algorithms in real-world scenarios.