Mean-field limit from general mixtures of experts to quantum neural networks

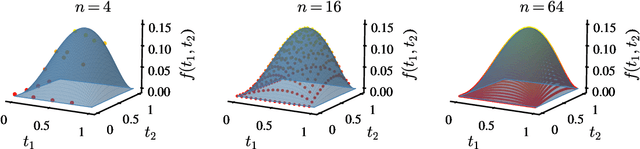
In this work, we study the asymptotic behavior of Mixture of Experts (MoE) trained via gradient flow on supervised learning problems. Our main result establishes the propagation of chaos for a MoE as the number of experts diverges. We demonstrate that the corresponding empirical measure of their parameters is close to a probability measure that solves a nonlinear continuity equation, and we provide an explicit convergence rate that depends solely on the number of experts. We apply our results to a MoE generated by a quantum neural network.

Trained quantum neural networks are Gaussian processes

We study quantum neural networks made by parametric one-qubit gates and fixed two-qubit gates in the limit of infinite width, where the generated function is the expectation value of the sum of single-qubit observables over all the qubits. First, we prove that the probability distribution of the function generated by the untrained network with randomly initialized parameters converges in distribution to a Gaussian process whenever each measured qubit is correlated only with few other measured qubits. Then, we analytically characterize the training of the network via gradient descent with square loss on supervised learning problems. We prove that, as long as the network is not affected by barren plateaus, the trained network can perfectly fit the training set and that the probability distribution of the function generated after training still converges in distribution to a Gaussian process. Finally, we consider the statistical noise of the measurement at the output of the network and prove that a polynomial number of measurements is sufficient for all the previous results to hold and that the network can always be trained in polynomial time.

Quantum algorithms for group convolution, cross-correlation, and equivariant transformations

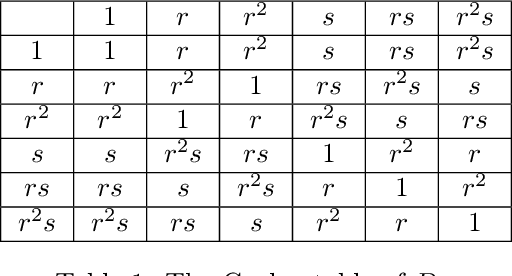
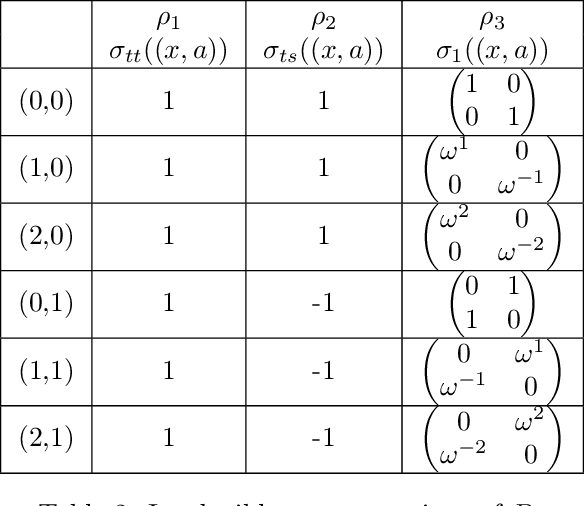
Group convolutions and cross-correlations, which are equivariant to the actions of group elements, are commonly used in mathematics to analyze or take advantage of symmetries inherent in a given problem setting. Here, we provide efficient quantum algorithms for performing linear group convolutions and cross-correlations on data stored as quantum states. Runtimes for our algorithms are logarithmic in the dimension of the group thus offering an exponential speedup compared to classical algorithms when input data is provided as a quantum state and linear operations are well conditioned. Motivated by the rich literature on quantum algorithms for solving algebraic problems, our theoretical framework opens a path for quantizing many algorithms in machine learning and numerical methods that employ group operations.

Quantum Earth Mover's Distance: A New Approach to Learning Quantum Data

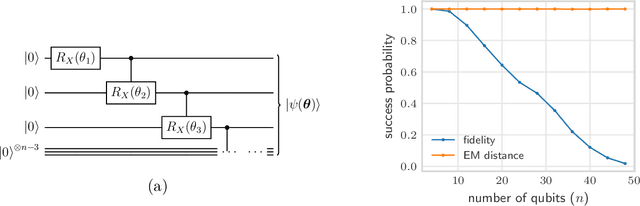
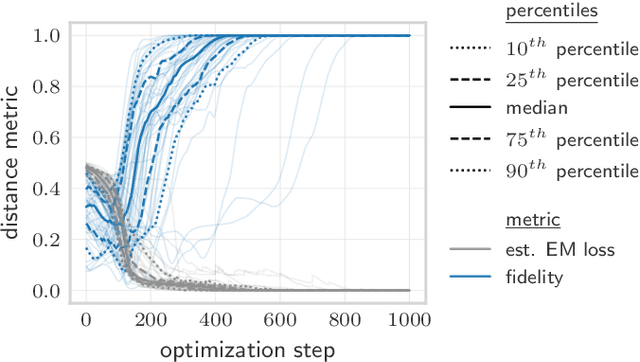
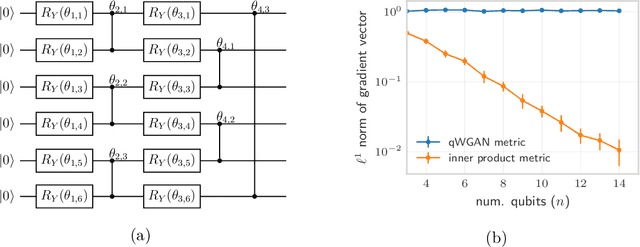
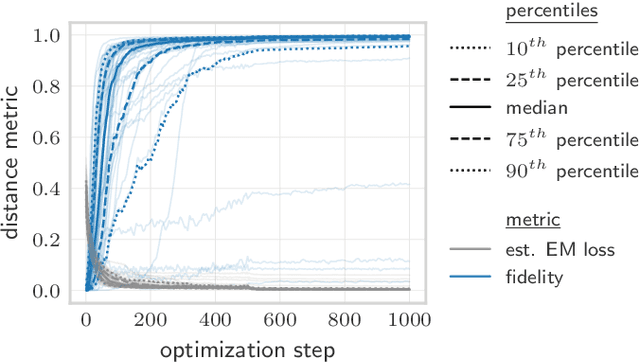
Quantifying how far the output of a learning algorithm is from its target is an essential task in machine learning. However, in quantum settings, the loss landscapes of commonly used distance metrics often produce undesirable outcomes such as poor local minima and exponentially decaying gradients. As a new approach, we consider here the quantum earth mover's (EM) or Wasserstein-1 distance, recently proposed in [De Palma et al., arXiv:2009.04469] as a quantum analog to the classical EM distance. We show that the quantum EM distance possesses unique properties, not found in other commonly used quantum distance metrics, that make quantum learning more stable and efficient. We propose a quantum Wasserstein generative adversarial network (qWGAN) which takes advantage of the quantum EM distance and provides an efficient means of performing learning on quantum data. Our qWGAN requires resources polynomial in the number of qubits, and our numerical experiments demonstrate that it is capable of learning a diverse set of quantum data.

Adversarial robustness guarantees for random deep neural networks

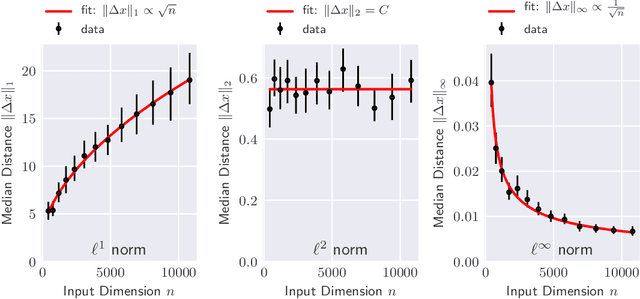
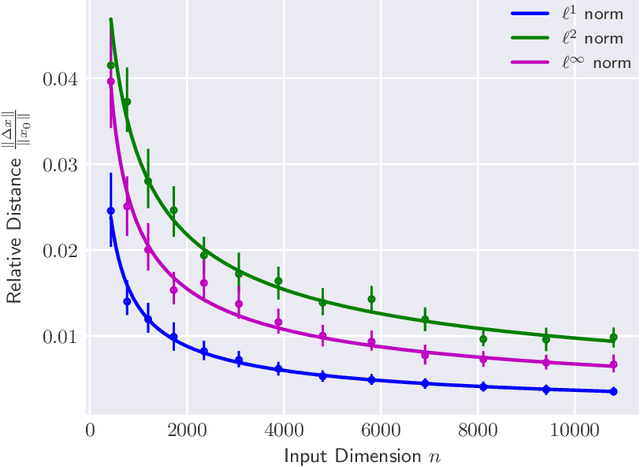
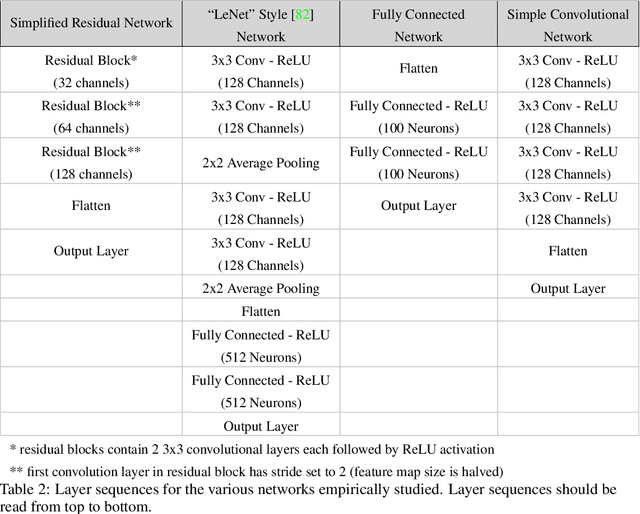
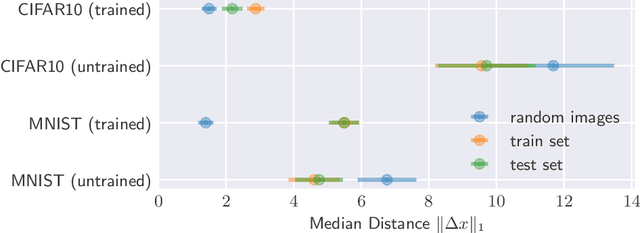
The reliability of most deep learning algorithms is fundamentally challenged by the existence of adversarial examples, which are incorrectly classified inputs that are extremely close to a correctly classified input. We study adversarial examples for deep neural networks with random weights and biases and prove that the $\ell^1$ distance of any given input from the classification boundary scales at least as $\sqrt{n}$, where $n$ is the dimension of the input. We also extend our proof to cover all the $\ell^p$ norms. Our results constitute a fundamental advance in the study of adversarial examples, and encompass a wide variety of architectures, which include any combination of convolutional or fully connected layers with skipped connections and pooling. We validate our results with experiments on both random deep neural networks and deep neural networks trained on the MNIST and CIFAR10 datasets. Given the results of our experiments on MNIST and CIFAR10, we conjecture that the proof of our adversarial robustness guarantee can be extended to trained deep neural networks. This extension will open the way to a thorough theoretical study of neural network robustness by classifying the relation between network architecture and adversarial distance.

Deep neural networks are biased towards simple functions

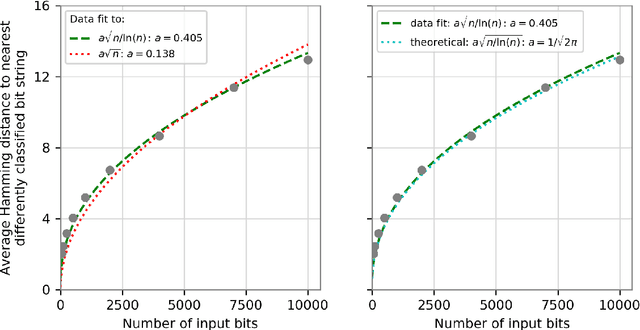
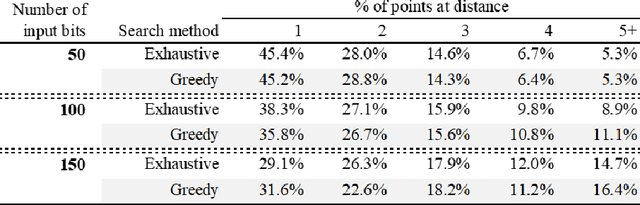
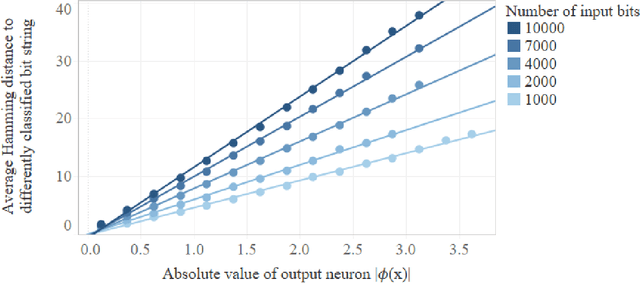
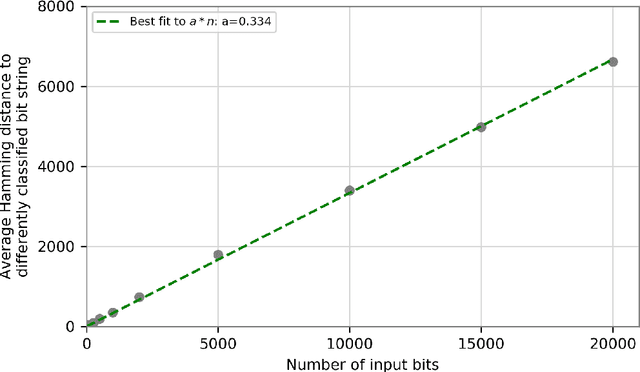
We prove that the binary classifiers of bit strings generated by random wide deep neural networks are biased towards simple functions. The simplicity is captured by the following two properties. For any given input bit string, the average Hamming distance of the closest input bit string with a different classification is at least $\sqrt{n\left/\left(2\pi\ln n\right)\right.}$, where $n$ is the length of the string. Moreover, if the bits of the initial string are flipped randomly, the average number of flips required to change the classification grows linearly with $n$. On the contrary, for a uniformly random binary classifier, the average Hamming distance of the closest input bit string with a different classification is one, and the average number of random flips required to change the classification is two. These results are confirmed by numerical experiments on deep neural networks with two hidden layers, and settle the conjecture stating that random deep neural networks are biased towards simple functions. The conjecture that random deep neural networks are biased towards simple functions was proposed and numerically explored in [Valle P\'erez et al., arXiv:1805.08522] to explain the unreasonably good generalization properties of deep learning algorithms. By providing a precise characterization of the form of this bias towards simplicity, our results open the way to a rigorous proof of the generalization properties of deep learning algorithms in real-world scenarios.