Local Binary and Multiclass SVMs Trained on a Quantum Annealer

Support vector machines (SVMs) are widely used machine learning models (e.g., in remote sensing), with formulations for both classification and regression tasks. In the last years, with the advent of working quantum annealers, hybrid SVM models characterised by quantum training and classical execution have been introduced. These models have demonstrated comparable performance to their classical counterparts. However, they are limited in the training set size due to the restricted connectivity of the current quantum annealers. Hence, to take advantage of large datasets (like those related to Earth observation), a strategy is required. In the classical domain, local SVMs, namely, SVMs trained on the data samples selected by a k-nearest neighbors model, have already proven successful. Here, the local application of quantum-trained SVM models is proposed and empirically assessed. In particular, this approach allows overcoming the constraints on the training set size of the quantum-trained models while enhancing their performance. In practice, the FaLK-SVM method, designed for efficient local SVMs, has been combined with quantum-trained SVM models for binary and multiclass classification. In addition, for comparison, FaLK-SVM has been interfaced for the first time with a classical single-step multiclass SVM model (CS SVM). Concerning the empirical evaluation, D-Wave's quantum annealers and real-world datasets taken from the remote sensing domain have been employed. The results have shown the effectiveness and scalability of the proposed approach, but also its practical applicability in a real-world large-scale scenario.

A general learning scheme for classical and quantum Ising machines

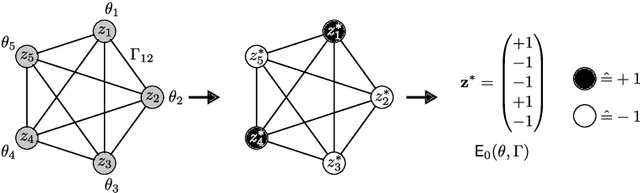
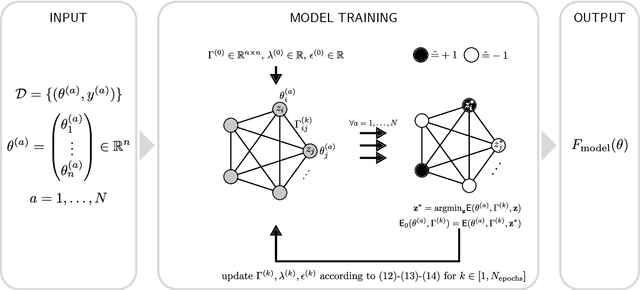
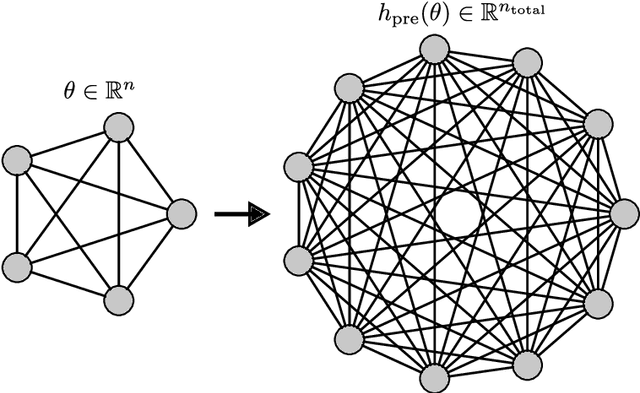
An Ising machine is any hardware specifically designed for finding the ground state of the Ising model. Relevant examples are coherent Ising machines and quantum annealers. In this paper, we propose a new machine learning model that is based on the Ising structure and can be efficiently trained using gradient descent. We provide a mathematical characterization of the training process, which is based upon optimizing a loss function whose partial derivatives are not explicitly calculated but estimated by the Ising machine itself. Moreover, we present some experimental results on the training and execution of the proposed learning model. These results point out new possibilities offered by Ising machines for different learning tasks. In particular, in the quantum realm, the quantum resources are used for both the execution and the training of the model, providing a promising perspective in quantum machine learning.