Theory for Equivariant Quantum Neural Networks

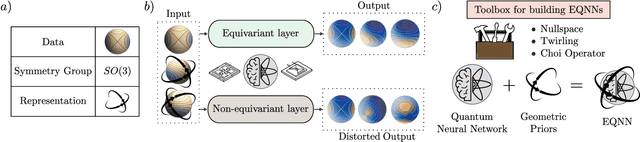
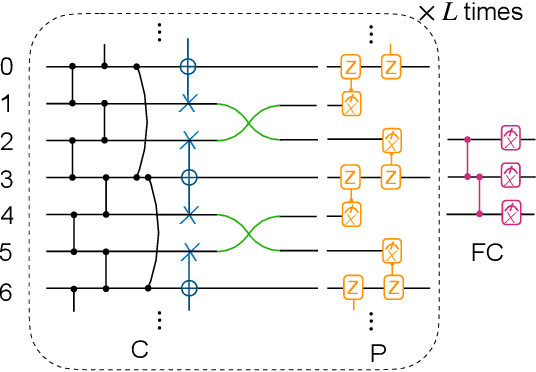
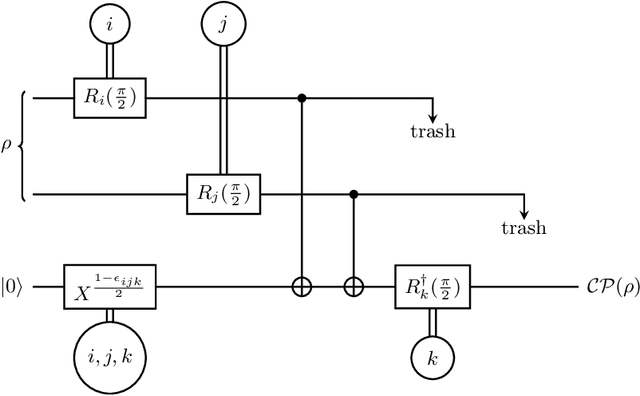
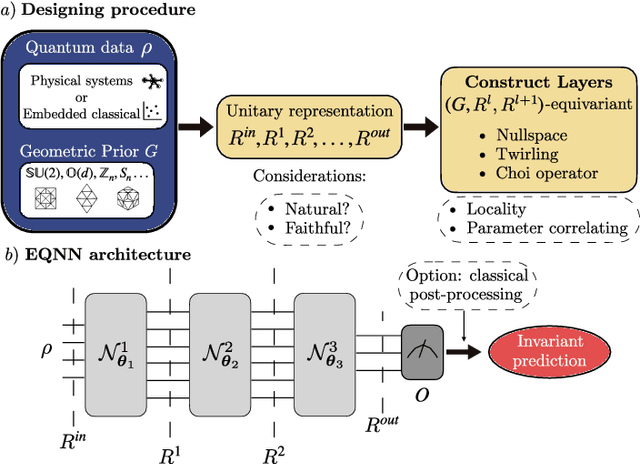
Most currently used quantum neural network architectures have little-to-no inductive biases, leading to trainability and generalization issues. Inspired by a similar problem, recent breakthroughs in classical machine learning address this crux by creating models encoding the symmetries of the learning task. This is materialized through the usage of equivariant neural networks whose action commutes with that of the symmetry. In this work, we import these ideas to the quantum realm by presenting a general theoretical framework to understand, classify, design and implement equivariant quantum neural networks. As a special implementation, we show how standard quantum convolutional neural networks (QCNN) can be generalized to group-equivariant QCNNs where both the convolutional and pooling layers are equivariant under the relevant symmetry group. Our framework can be readily applied to virtually all areas of quantum machine learning, and provides hope to alleviate central challenges such as barren plateaus, poor local minima, and sample complexity.

Representation Theory for Geometric Quantum Machine Learning

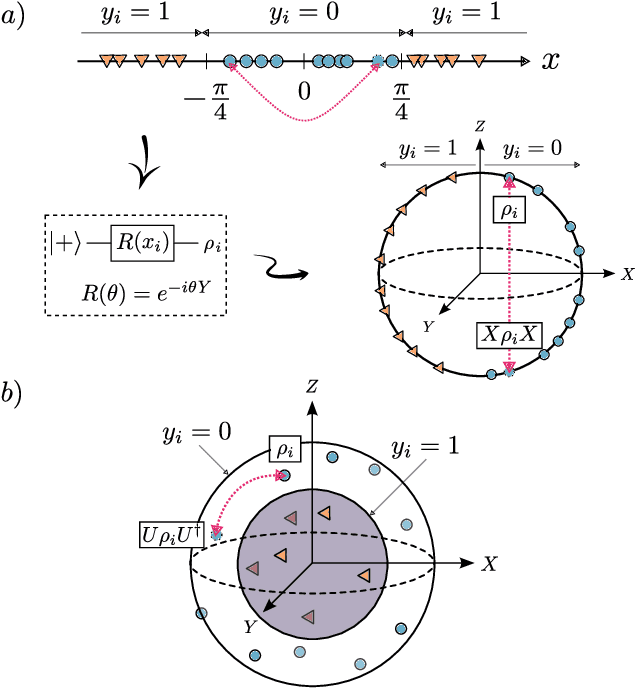
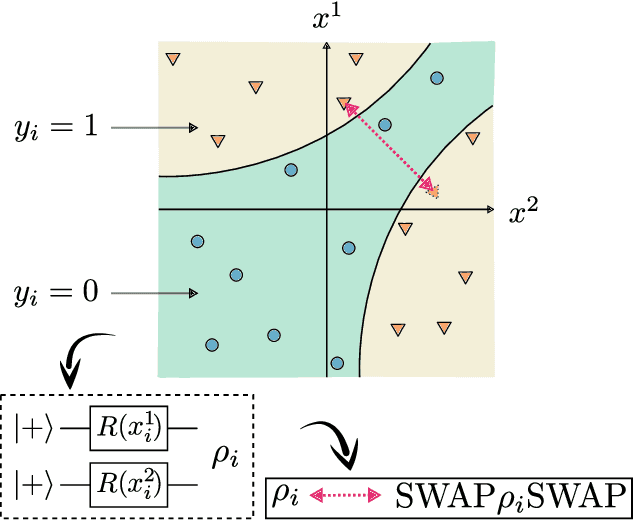
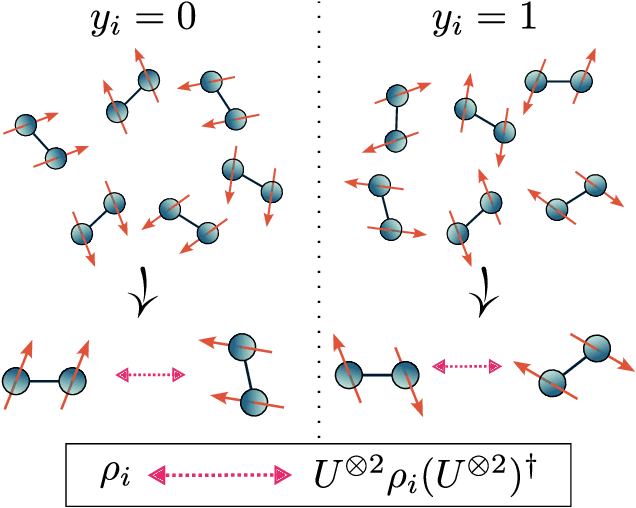
Recent advances in classical machine learning have shown that creating models with inductive biases encoding the symmetries of a problem can greatly improve performance. Importation of these ideas, combined with an existing rich body of work at the nexus of quantum theory and symmetry, has given rise to the field of Geometric Quantum Machine Learning (GQML). Following the success of its classical counterpart, it is reasonable to expect that GQML will play a crucial role in developing problem-specific and quantum-aware models capable of achieving a computational advantage. Despite the simplicity of the main idea of GQML -- create architectures respecting the symmetries of the data -- its practical implementation requires a significant amount of knowledge of group representation theory. We present an introduction to representation theory tools from the optics of quantum learning, driven by key examples involving discrete and continuous groups. These examples are sewn together by an exposition outlining the formal capture of GQML symmetries via "label invariance under the action of a group representation", a brief (but rigorous) tour through finite and compact Lie group representation theory, a reexamination of ubiquitous tools like Haar integration and twirling, and an overview of some successful strategies for detecting symmetries.

Quantum algorithms for group convolution, cross-correlation, and equivariant transformations

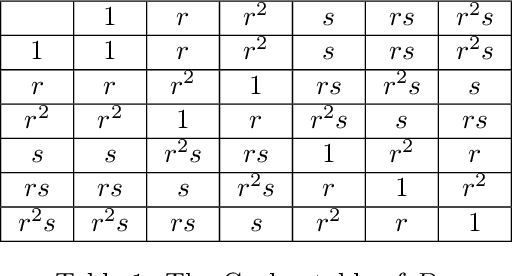
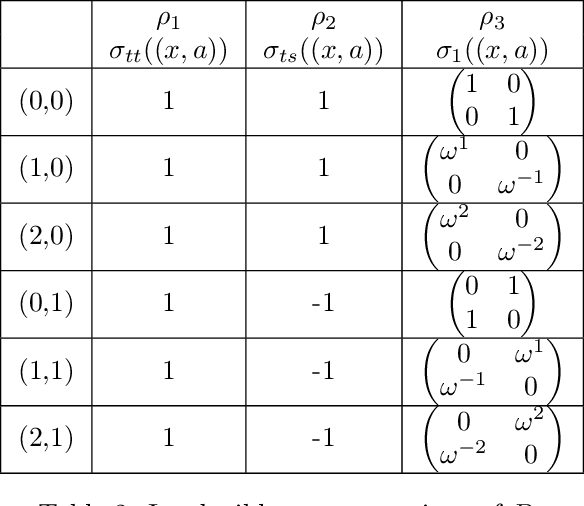
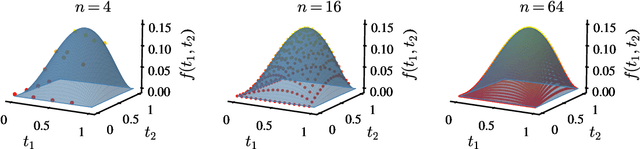
Group convolutions and cross-correlations, which are equivariant to the actions of group elements, are commonly used in mathematics to analyze or take advantage of symmetries inherent in a given problem setting. Here, we provide efficient quantum algorithms for performing linear group convolutions and cross-correlations on data stored as quantum states. Runtimes for our algorithms are logarithmic in the dimension of the group thus offering an exponential speedup compared to classical algorithms when input data is provided as a quantum state and linear operations are well conditioned. Motivated by the rich literature on quantum algorithms for solving algebraic problems, our theoretical framework opens a path for quantizing many algorithms in machine learning and numerical methods that employ group operations.