Quantum algorithms for group convolution, cross-correlation, and equivariant transformations
Paper and Code
Sep 23, 2021
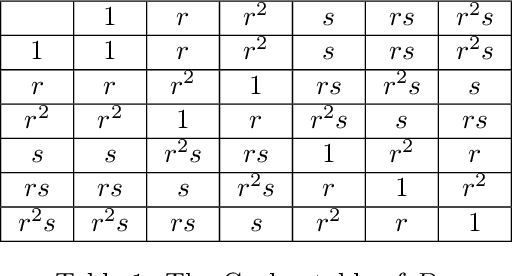
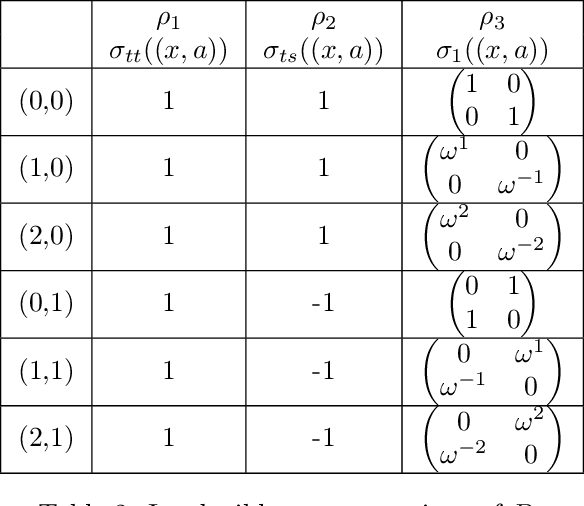
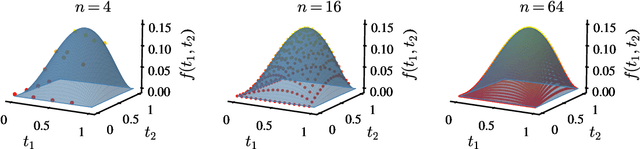
Group convolutions and cross-correlations, which are equivariant to the actions of group elements, are commonly used in mathematics to analyze or take advantage of symmetries inherent in a given problem setting. Here, we provide efficient quantum algorithms for performing linear group convolutions and cross-correlations on data stored as quantum states. Runtimes for our algorithms are logarithmic in the dimension of the group thus offering an exponential speedup compared to classical algorithms when input data is provided as a quantum state and linear operations are well conditioned. Motivated by the rich literature on quantum algorithms for solving algebraic problems, our theoretical framework opens a path for quantizing many algorithms in machine learning and numerical methods that employ group operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge