Scalable Thermodynamic Second-order Optimization

Many hardware proposals have aimed to accelerate inference in AI workloads. Less attention has been paid to hardware acceleration of training, despite the enormous societal impact of rapid training of AI models. Physics-based computers, such as thermodynamic computers, offer an efficient means to solve key primitives in AI training algorithms. Optimizers that normally would be computationally out-of-reach (e.g., due to expensive matrix inversions) on digital hardware could be unlocked with physics-based hardware. In this work, we propose a scalable algorithm for employing thermodynamic computers to accelerate a popular second-order optimizer called Kronecker-factored approximate curvature (K-FAC). Our asymptotic complexity analysis predicts increasing advantage with our algorithm as $n$, the number of neurons per layer, increases. Numerical experiments show that even under significant quantization noise, the benefits of second-order optimization can be preserved. Finally, we predict substantial speedups for large-scale vision and graph problems based on realistic hardware characteristics.

Thermodynamic Bayesian Inference

A fully Bayesian treatment of complicated predictive models (such as deep neural networks) would enable rigorous uncertainty quantification and the automation of higher-level tasks including model selection. However, the intractability of sampling Bayesian posteriors over many parameters inhibits the use of Bayesian methods where they are most needed. Thermodynamic computing has emerged as a paradigm for accelerating operations used in machine learning, such as matrix inversion, and is based on the mapping of Langevin equations to the dynamics of noisy physical systems. Hence, it is natural to consider the implementation of Langevin sampling algorithms on thermodynamic devices. In this work we propose electronic analog devices that sample from Bayesian posteriors by realizing Langevin dynamics physically. Circuit designs are given for sampling the posterior of a Gaussian-Gaussian model and for Bayesian logistic regression, and are validated by simulations. It is shown, under reasonable assumptions, that the Bayesian posteriors for these models can be sampled in time scaling with $\ln(d)$, where $d$ is dimension. For the Gaussian-Gaussian model, the energy cost is shown to scale with $ d \ln(d)$. These results highlight the potential for fast, energy-efficient Bayesian inference using thermodynamic computing.

Thermodynamic Natural Gradient Descent

Second-order training methods have better convergence properties than gradient descent but are rarely used in practice for large-scale training due to their computational overhead. This can be viewed as a hardware limitation (imposed by digital computers). Here we show that natural gradient descent (NGD), a second-order method, can have a similar computational complexity per iteration to a first-order method, when employing appropriate hardware. We present a new hybrid digital-analog algorithm for training neural networks that is equivalent to NGD in a certain parameter regime but avoids prohibitively costly linear system solves. Our algorithm exploits the thermodynamic properties of an analog system at equilibrium, and hence requires an analog thermodynamic computer. The training occurs in a hybrid digital-analog loop, where the gradient and Fisher information matrix (or any other positive semi-definite curvature matrix) are calculated at given time intervals while the analog dynamics take place. We numerically demonstrate the superiority of this approach over state-of-the-art digital first- and second-order training methods on classification tasks and language model fine-tuning tasks.

A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

Thermodynamic Computing System for AI Applications

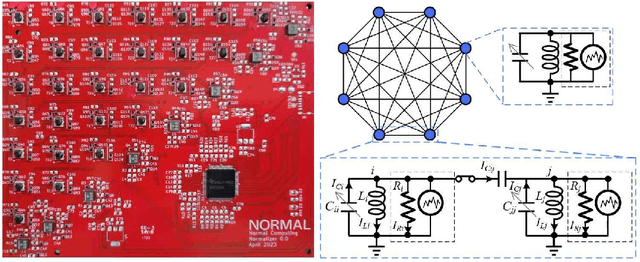
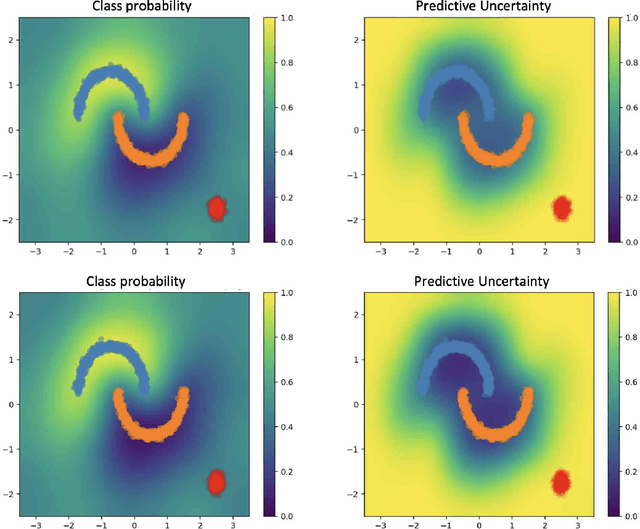
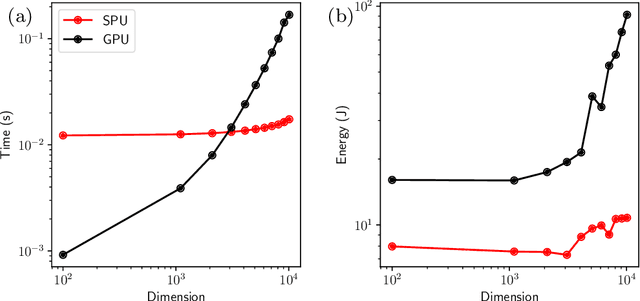
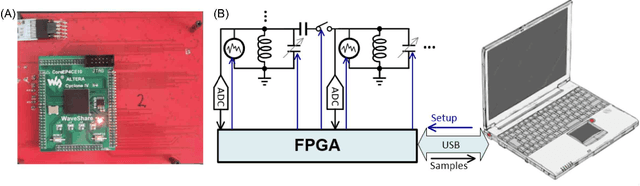
Recent breakthroughs in artificial intelligence (AI) algorithms have highlighted the need for novel computing hardware in order to truly unlock the potential for AI. Physics-based hardware, such as thermodynamic computing, has the potential to provide a fast, low-power means to accelerate AI primitives, especially generative AI and probabilistic AI. In this work, we present the first continuous-variable thermodynamic computer, which we call the stochastic processing unit (SPU). Our SPU is composed of RLC circuits, as unit cells, on a printed circuit board, with 8 unit cells that are all-to-all coupled via switched capacitances. It can be used for either sampling or linear algebra primitives, and we demonstrate Gaussian sampling and matrix inversion on our hardware. The latter represents the first thermodynamic linear algebra experiment. We also illustrate the applicability of the SPU to uncertainty quantification for neural network classification. We envision that this hardware, when scaled up in size, will have significant impact on accelerating various probabilistic AI applications.

The power and limitations of learning quantum dynamics incoherently

Quantum process learning is emerging as an important tool to study quantum systems. While studied extensively in coherent frameworks, where the target and model system can share quantum information, less attention has been paid to whether the dynamics of quantum systems can be learned without the system and target directly interacting. Such incoherent frameworks are practically appealing since they open up methods of transpiling quantum processes between the different physical platforms without the need for technically challenging hybrid entanglement schemes. Here we provide bounds on the sample complexity of learning unitary processes incoherently by analyzing the number of measurements that are required to emulate well-established coherent learning strategies. We prove that if arbitrary measurements are allowed, then any efficiently representable unitary can be efficiently learned within the incoherent framework; however, when restricted to shallow-depth measurements only low-entangling unitaries can be learned. We demonstrate our incoherent learning algorithm for low entangling unitaries by successfully learning a 16-qubit unitary on \texttt{ibmq\_kolkata}, and further demonstrate the scalabilty of our proposed algorithm through extensive numerical experiments.

Challenges and Opportunities in Quantum Machine Learning

At the intersection of machine learning and quantum computing, Quantum Machine Learning (QML) has the potential of accelerating data analysis, especially for quantum data, with applications for quantum materials, biochemistry, and high-energy physics. Nevertheless, challenges remain regarding the trainability of QML models. Here we review current methods and applications for QML. We highlight differences between quantum and classical machine learning, with a focus on quantum neural networks and quantum deep learning. Finally, we discuss opportunities for quantum advantage with QML.

Thermodynamic AI and the fluctuation frontier

Many Artificial Intelligence (AI) algorithms are inspired by physics and employ stochastic fluctuations. We connect these physics-inspired AI algorithms by unifying them under a single mathematical framework that we call Thermodynamic AI. Seemingly disparate algorithmic classes can be described by this framework, for example, (1) Generative diffusion models, (2) Bayesian neural networks, (3) Monte Carlo sampling and (4) Simulated annealing. Such Thermodynamic AI algorithms are currently run on digital hardware, ultimately limiting their scalability and overall potential. Stochastic fluctuations naturally occur in physical thermodynamic systems, and such fluctuations can be viewed as a computational resource. Hence, we propose a novel computing paradigm, where software and hardware become inseparable. Our algorithmic unification allows us to identify a single full-stack paradigm, involving Thermodynamic AI hardware, that could accelerate such algorithms. We contrast Thermodynamic AI hardware with quantum computing where noise is a roadblock rather than a resource. Thermodynamic AI hardware can be viewed as a novel form of computing, since it uses a novel fundamental building block. We identify stochastic bits (s-bits) and stochastic modes (s-modes) as the respective building blocks for discrete and continuous Thermodynamic AI hardware. In addition to these stochastic units, Thermodynamic AI hardware employs a Maxwell's demon device that guides the system to produce non-trivial states. We provide a few simple physical architectures for building these devices and we develop a formalism for programming the hardware via gate sequences. We hope to stimulate discussion around this new computing paradigm. Beyond acceleration, we believe it will impact the design of both hardware and algorithms, while also deepening our understanding of the connection between physics and intelligence.

Resource frugal optimizer for quantum machine learning

Quantum-enhanced data science, also known as quantum machine learning (QML), is of growing interest as an application of near-term quantum computers. Variational QML algorithms have the potential to solve practical problems on real hardware, particularly when involving quantum data. However, training these algorithms can be challenging and calls for tailored optimization procedures. Specifically, QML applications can require a large shot-count overhead due to the large datasets involved. In this work, we advocate for simultaneous random sampling over both the dataset as well as the measurement operators that define the loss function. We consider a highly general loss function that encompasses many QML applications, and we show how to construct an unbiased estimator of its gradient. This allows us to propose a shot-frugal gradient descent optimizer called Refoqus (REsource Frugal Optimizer for QUantum Stochastic gradient descent). Our numerics indicate that Refoqus can save several orders of magnitude in shot cost, even relative to optimizers that sample over measurement operators alone.

Theory for Equivariant Quantum Neural Networks

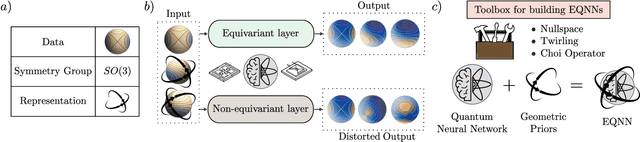
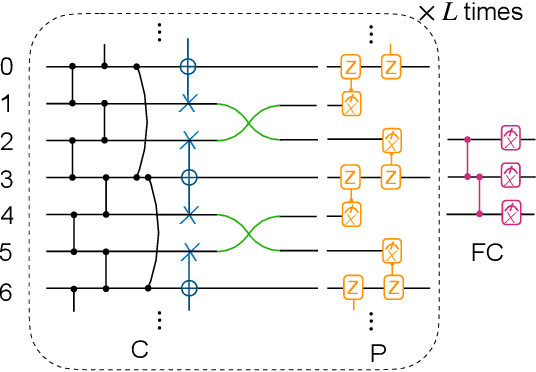
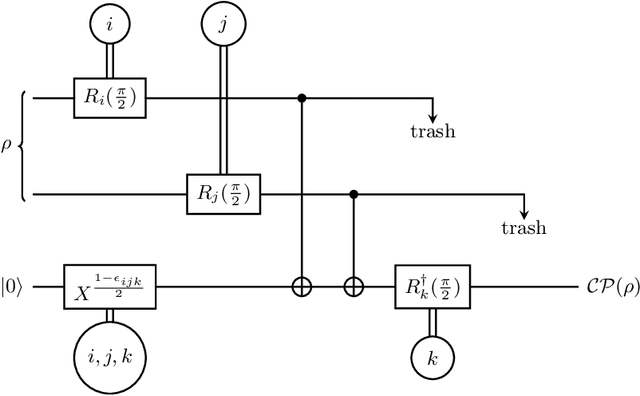
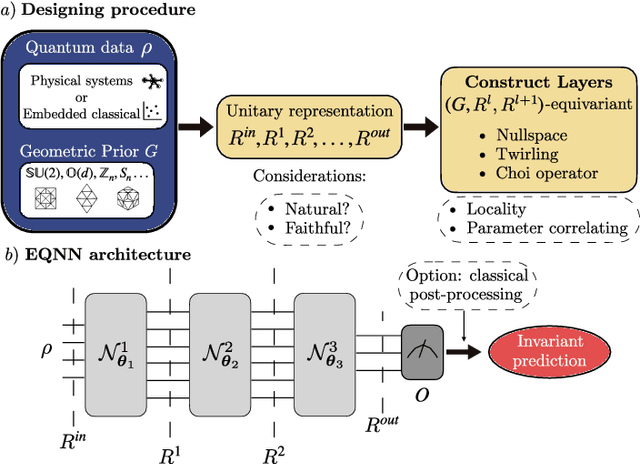
Most currently used quantum neural network architectures have little-to-no inductive biases, leading to trainability and generalization issues. Inspired by a similar problem, recent breakthroughs in classical machine learning address this crux by creating models encoding the symmetries of the learning task. This is materialized through the usage of equivariant neural networks whose action commutes with that of the symmetry. In this work, we import these ideas to the quantum realm by presenting a general theoretical framework to understand, classify, design and implement equivariant quantum neural networks. As a special implementation, we show how standard quantum convolutional neural networks (QCNN) can be generalized to group-equivariant QCNNs where both the convolutional and pooling layers are equivariant under the relevant symmetry group. Our framework can be readily applied to virtually all areas of quantum machine learning, and provides hope to alleviate central challenges such as barren plateaus, poor local minima, and sample complexity.