Thermodynamic Computing System for AI Applications

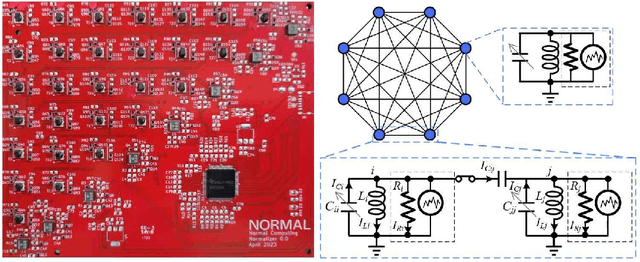
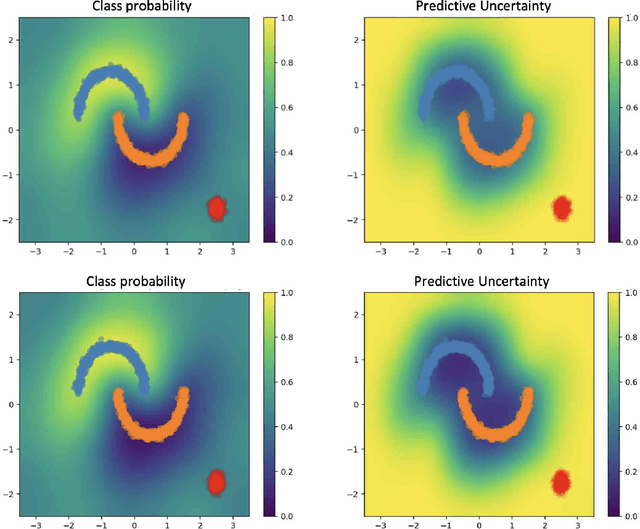
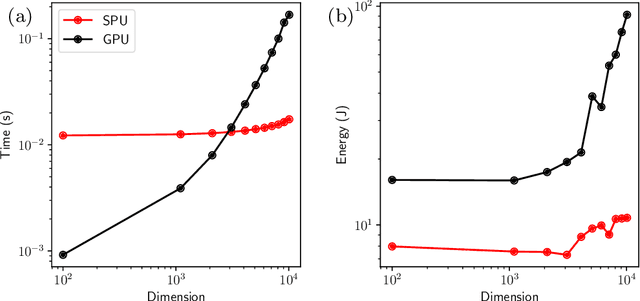
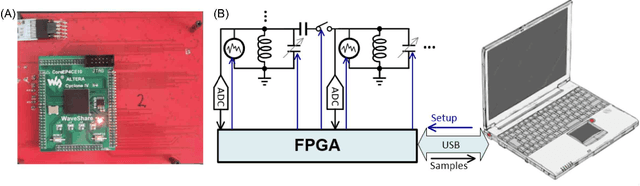
Recent breakthroughs in artificial intelligence (AI) algorithms have highlighted the need for novel computing hardware in order to truly unlock the potential for AI. Physics-based hardware, such as thermodynamic computing, has the potential to provide a fast, low-power means to accelerate AI primitives, especially generative AI and probabilistic AI. In this work, we present the first continuous-variable thermodynamic computer, which we call the stochastic processing unit (SPU). Our SPU is composed of RLC circuits, as unit cells, on a printed circuit board, with 8 unit cells that are all-to-all coupled via switched capacitances. It can be used for either sampling or linear algebra primitives, and we demonstrate Gaussian sampling and matrix inversion on our hardware. The latter represents the first thermodynamic linear algebra experiment. We also illustrate the applicability of the SPU to uncertainty quantification for neural network classification. We envision that this hardware, when scaled up in size, will have significant impact on accelerating various probabilistic AI applications.

Resource frugal optimizer for quantum machine learning

Quantum-enhanced data science, also known as quantum machine learning (QML), is of growing interest as an application of near-term quantum computers. Variational QML algorithms have the potential to solve practical problems on real hardware, particularly when involving quantum data. However, training these algorithms can be challenging and calls for tailored optimization procedures. Specifically, QML applications can require a large shot-count overhead due to the large datasets involved. In this work, we advocate for simultaneous random sampling over both the dataset as well as the measurement operators that define the loss function. We consider a highly general loss function that encompasses many QML applications, and we show how to construct an unbiased estimator of its gradient. This allows us to propose a shot-frugal gradient descent optimizer called Refoqus (REsource Frugal Optimizer for QUantum Stochastic gradient descent). Our numerics indicate that Refoqus can save several orders of magnitude in shot cost, even relative to optimizers that sample over measurement operators alone.

Inference-Based Quantum Sensing

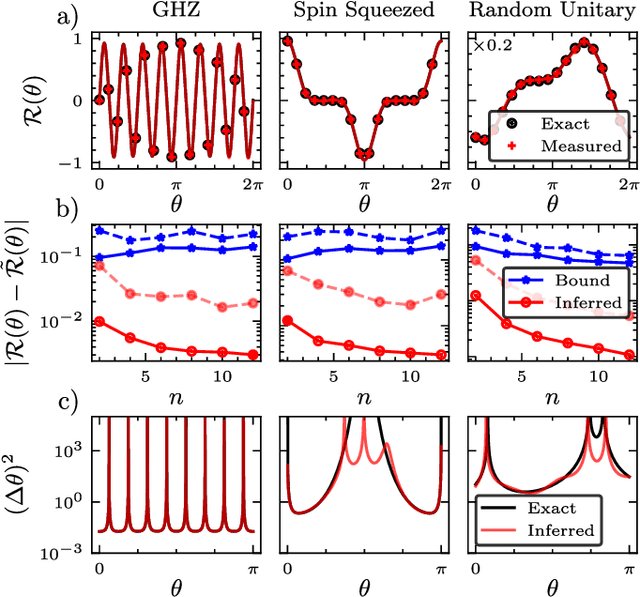
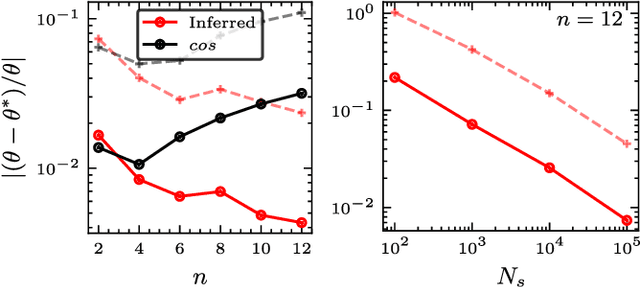
In a standard Quantum Sensing (QS) task one aims at estimating an unknown parameter $\theta$, encoded into an $n$-qubit probe state, via measurements of the system. The success of this task hinges on the ability to correlate changes in the parameter to changes in the system response $\mathcal{R}(\theta)$ (i.e., changes in the measurement outcomes). For simple cases the form of $\mathcal{R}(\theta)$ is known, but the same cannot be said for realistic scenarios, as no general closed-form expression exists. In this work we present an inference-based scheme for QS. We show that, for a general class of unitary families of encoding, $\mathcal{R}(\theta)$ can be fully characterized by only measuring the system response at $2n+1$ parameters. In turn, this allows us to infer the value of an unknown parameter given the measured response, as well as to determine the sensitivity of the sensing scheme, which characterizes its overall performance. We show that inference error is, with high probability, smaller than $\delta$, if one measures the system response with a number of shots that scales only as $\Omega(\log^3(n)/\delta^2)$. Furthermore, the framework presented can be broadly applied as it remains valid for arbitrary probe states and measurement schemes, and, even holds in the presence of quantum noise. We also discuss how to extend our results beyond unitary families. Finally, to showcase our method we implement it for a QS task on real quantum hardware, and in numerical simulations.

Covariance matrix preparation for quantum principal component analysis

Principal component analysis (PCA) is a dimensionality reduction method in data analysis that involves diagonalizing the covariance matrix of the dataset. Recently, quantum algorithms have been formulated for PCA based on diagonalizing a density matrix. These algorithms assume that the covariance matrix can be encoded in a density matrix, but a concrete protocol for this encoding has been lacking. Our work aims to address this gap. Assuming amplitude encoding of the data, with the data given by the ensemble $\{p_i,| \psi_i \rangle\}$, then one can easily prepare the ensemble average density matrix $\overline{\rho} = \sum_i p_i |\psi_i\rangle \langle \psi_i |$. We first show that $\overline{\rho}$ is precisely the covariance matrix whenever the dataset is centered. For quantum datasets, we exploit global phase symmetry to argue that there always exists a centered dataset consistent with $\overline{\rho}$, and hence $\overline{\rho}$ can always be interpreted as a covariance matrix. This provides a simple means for preparing the covariance matrix for arbitrary quantum datasets or centered classical datasets. For uncentered classical datasets, our method is so-called "PCA without centering", which we interpret as PCA on a symmetrized dataset. We argue that this closely corresponds to standard PCA, and we derive equations and inequalities that bound the deviation of the spectrum obtained with our method from that of standard PCA. We numerically illustrate our method for the MNIST handwritten digit dataset. We also argue that PCA on quantum datasets is natural and meaningful, and we numerically implement our method for molecular ground-state datasets.