Scalable quantum dynamics compilation via quantum machine learning

Quantum dynamics compilation is an important task for improving quantum simulation efficiency: It aims to synthesize multi-qubit target dynamics into a circuit consisting of as few elementary gates as possible. Compared to deterministic methods such as Trotterization, variational quantum compilation (VQC) methods employ variational optimization to reduce gate costs while maintaining high accuracy. In this work, we explore the potential of a VQC scheme by making use of out-of-distribution generalization results in quantum machine learning (QML): By learning the action of a given many-body dynamics on a small data set of product states, we can obtain a unitary circuit that generalizes to highly entangled states such as the Haar random states. The efficiency in training allows us to use tensor network methods to compress such time-evolved product states by exploiting their low entanglement features. Our approach exceeds state-of-the-art compilation results in both system size and accuracy in one dimension ($1$D). For the first time, we extend VQC to systems on two-dimensional (2D) strips with a quasi-1D treatment, demonstrating a significant resource advantage over standard Trotterization methods, highlighting the method's promise for advancing quantum simulation tasks on near-term quantum processors.

Quantum Convolutional Neural Networks are (Effectively) Classically Simulable

Quantum Convolutional Neural Networks (QCNNs) are widely regarded as a promising model for Quantum Machine Learning (QML). In this work we tie their heuristic success to two facts. First, that when randomly initialized, they can only operate on the information encoded in low-bodyness measurements of their input states. And second, that they are commonly benchmarked on "locally-easy'' datasets whose states are precisely classifiable by the information encoded in these low-bodyness observables subspace. We further show that the QCNN's action on this subspace can be efficiently classically simulated by a classical algorithm equipped with Pauli shadows on the dataset. Indeed, we present a shadow-based simulation of QCNNs on up-to $1024$ qubits for phases of matter classification. Our results can then be understood as highlighting a deeper symptom of QML: Models could only be showing heuristic success because they are benchmarked on simple problems, for which their action can be classically simulated. This insight points to the fact that non-trivial datasets are a truly necessary ingredient for moving forward with QML. To finish, we discuss how our results can be extrapolated to classically simulate other architectures.

A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

Quantum computer-enabled receivers for optical communication

Optical communication is the standard for high-bandwidth information transfer in today's digital age. The increasing demand for bandwidth has led to the maturation of coherent transceivers that use phase- and amplitude-modulated optical signals to encode more bits of information per transmitted pulse. Such encoding schemes achieve higher information density, but also require more complicated receivers to discriminate the signaling states. In fact, achieving the ultimate limit of optical communication capacity, especially in the low light regime, requires coherent joint detection of multiple pulses. Despite their superiority, such joint detection receivers are not in widespread use because of the difficulty of constructing them in the optical domain. In this work we describe how optomechanical transduction of phase information from coherent optical pulses to superconducting qubit states followed by the execution of trained short-depth variational quantum circuits can perform joint detection of communication codewords with error probabilities that surpass all classical, individual pulse detection receivers. Importantly, we utilize a model of optomechanical transduction that captures non-idealities such as thermal noise and loss in order to understand the transduction performance necessary to achieve a quantum advantage with such a scheme. We also execute the trained variational circuits on an IBM-Q device with the modeled transduced states as input to demonstrate that a quantum advantage is possible even with current levels of quantum computing hardware noise.

Challenges and Opportunities in Quantum Machine Learning

At the intersection of machine learning and quantum computing, Quantum Machine Learning (QML) has the potential of accelerating data analysis, especially for quantum data, with applications for quantum materials, biochemistry, and high-energy physics. Nevertheless, challenges remain regarding the trainability of QML models. Here we review current methods and applications for QML. We highlight differences between quantum and classical machine learning, with a focus on quantum neural networks and quantum deep learning. Finally, we discuss opportunities for quantum advantage with QML.

Resource frugal optimizer for quantum machine learning

Quantum-enhanced data science, also known as quantum machine learning (QML), is of growing interest as an application of near-term quantum computers. Variational QML algorithms have the potential to solve practical problems on real hardware, particularly when involving quantum data. However, training these algorithms can be challenging and calls for tailored optimization procedures. Specifically, QML applications can require a large shot-count overhead due to the large datasets involved. In this work, we advocate for simultaneous random sampling over both the dataset as well as the measurement operators that define the loss function. We consider a highly general loss function that encompasses many QML applications, and we show how to construct an unbiased estimator of its gradient. This allows us to propose a shot-frugal gradient descent optimizer called Refoqus (REsource Frugal Optimizer for QUantum Stochastic gradient descent). Our numerics indicate that Refoqus can save several orders of magnitude in shot cost, even relative to optimizers that sample over measurement operators alone.

Practical Black Box Hamiltonian Learning

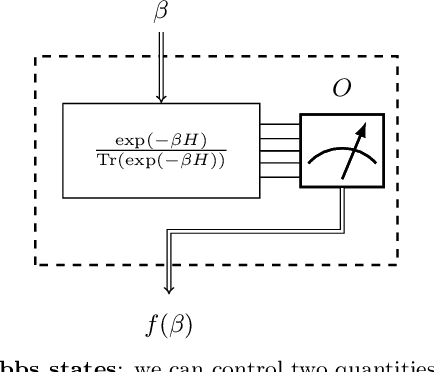
We study the problem of learning the parameters for the Hamiltonian of a quantum many-body system, given limited access to the system. In this work, we build upon recent approaches to Hamiltonian learning via derivative estimation. We propose a protocol that improves the scaling dependence of prior works, particularly with respect to parameters relating to the structure of the Hamiltonian (e.g., its locality $k$). Furthermore, by deriving exact bounds on the performance of our protocol, we are able to provide a precise numerical prescription for theoretically optimal settings of hyperparameters in our learning protocol, such as the maximum evolution time (when learning with unitary dynamics) or minimum temperature (when learning with Gibbs states). Thanks to these improvements, our protocol is practical for large problems: we demonstrate this with a numerical simulation of our protocol on an 80-qubit system.

Dynamical simulation via quantum machine learning with provable generalization

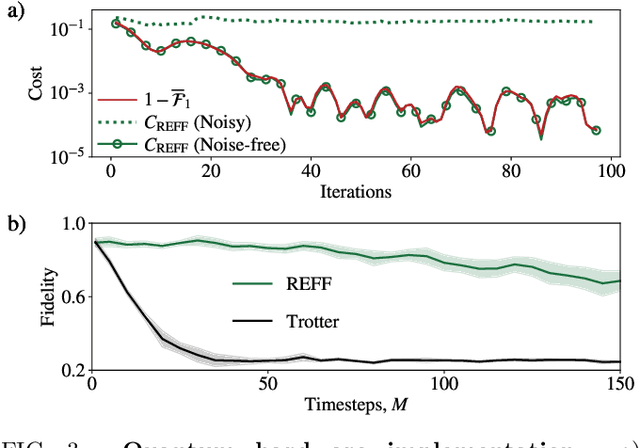
Much attention has been paid to dynamical simulation and quantum machine learning (QML) independently as applications for quantum advantage, while the possibility of using QML to enhance dynamical simulations has not been thoroughly investigated. Here we develop a framework for using QML methods to simulate quantum dynamics on near-term quantum hardware. We use generalization bounds, which bound the error a machine learning model makes on unseen data, to rigorously analyze the training data requirements of an algorithm within this framework. This provides a guarantee that our algorithm is resource-efficient, both in terms of qubit and data requirements. Our numerics exhibit efficient scaling with problem size, and we simulate 20 times longer than Trotterization on IBMQ-Bogota.

Out-of-distribution generalization for learning quantum dynamics

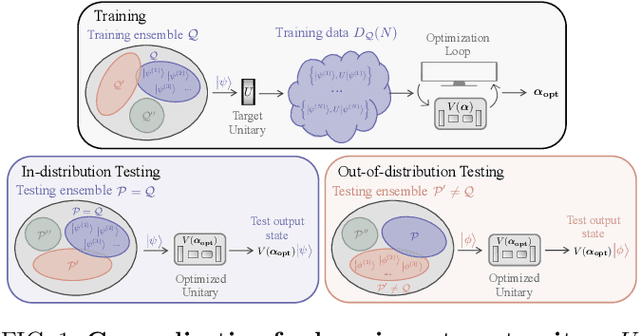
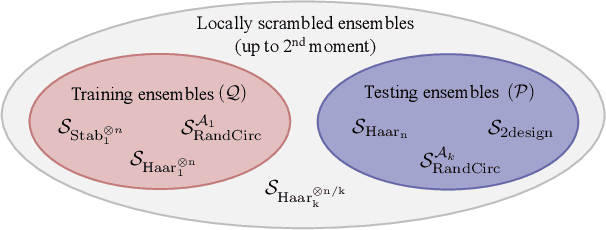
Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.

Covariance matrix preparation for quantum principal component analysis

Principal component analysis (PCA) is a dimensionality reduction method in data analysis that involves diagonalizing the covariance matrix of the dataset. Recently, quantum algorithms have been formulated for PCA based on diagonalizing a density matrix. These algorithms assume that the covariance matrix can be encoded in a density matrix, but a concrete protocol for this encoding has been lacking. Our work aims to address this gap. Assuming amplitude encoding of the data, with the data given by the ensemble $\{p_i,| \psi_i \rangle\}$, then one can easily prepare the ensemble average density matrix $\overline{\rho} = \sum_i p_i |\psi_i\rangle \langle \psi_i |$. We first show that $\overline{\rho}$ is precisely the covariance matrix whenever the dataset is centered. For quantum datasets, we exploit global phase symmetry to argue that there always exists a centered dataset consistent with $\overline{\rho}$, and hence $\overline{\rho}$ can always be interpreted as a covariance matrix. This provides a simple means for preparing the covariance matrix for arbitrary quantum datasets or centered classical datasets. For uncentered classical datasets, our method is so-called "PCA without centering", which we interpret as PCA on a symmetrized dataset. We argue that this closely corresponds to standard PCA, and we derive equations and inequalities that bound the deviation of the spectrum obtained with our method from that of standard PCA. We numerically illustrate our method for the MNIST handwritten digit dataset. We also argue that PCA on quantum datasets is natural and meaningful, and we numerically implement our method for molecular ground-state datasets.