Out-of-distribution generalization for learning quantum dynamics

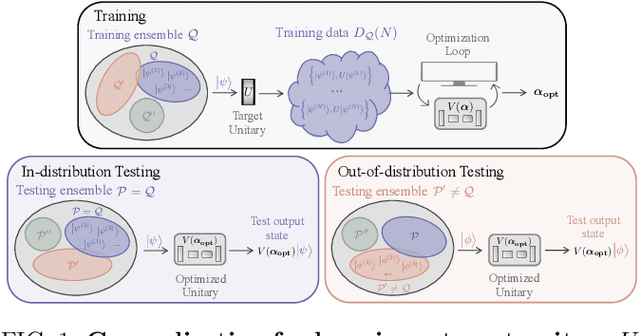
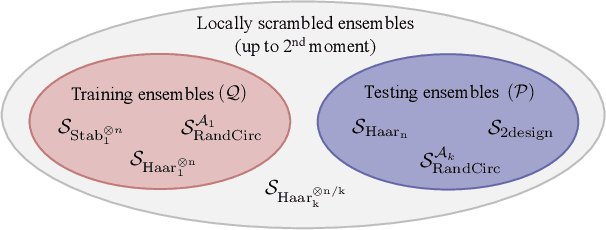
Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.