ClassiFIM: An Unsupervised Method To Detect Phase Transitions

Estimation of the Fisher Information Metric (FIM-estimation) is an important task that arises in unsupervised learning of phase transitions, a problem proposed by physicists. This work completes the definition of the task by defining rigorous evaluation metrics distMSE, distMSEPS, and distRE and introduces ClassiFIM, a novel machine learning method designed to solve the FIM-estimation task. Unlike existing methods for unsupervised learning of phase transitions, ClassiFIM directly estimates a well-defined quantity (the FIM), allowing it to be rigorously compared to any present and future other methods that estimate the same. ClassiFIM transforms a dataset for the FIM-estimation task into a dataset for an auxiliary binary classification task and involves selecting and training a model for the latter. We prove that the output of ClassiFIM approaches the exact FIM in the limit of infinite dataset size and under certain regularity conditions. We implement ClassiFIM on multiple datasets, including datasets describing classical and quantum phase transitions, and find that it achieves a good ground truth approximation with modest computational resources. Furthermore, we independently implement two alternative state-of-the-art methods for unsupervised estimation of phase transition locations on the same datasets and find that ClassiFIM predicts such locations at least as well as these other methods. To emphasize the generality of our method, we also propose and generate the MNIST-CNN dataset, which consists of the output of CNNs trained on MNIST for different hyperparameter choices. Using ClassiFIM on this dataset suggests there is a phase transition in the distribution of image-prediction pairs for CNNs trained on MNIST, demonstrating the broad scope of FIM-estimation beyond physics.

Dynamical simulation via quantum machine learning with provable generalization

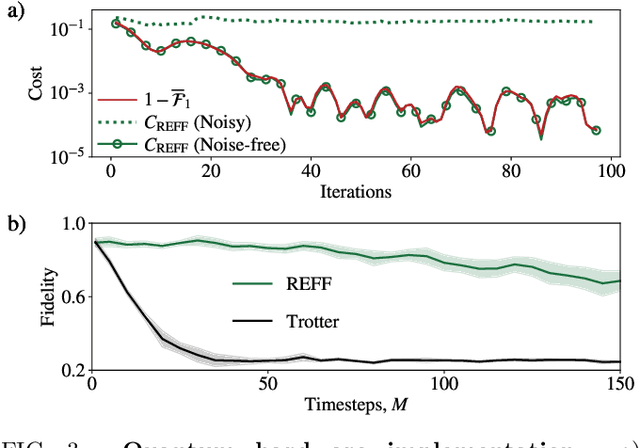
Much attention has been paid to dynamical simulation and quantum machine learning (QML) independently as applications for quantum advantage, while the possibility of using QML to enhance dynamical simulations has not been thoroughly investigated. Here we develop a framework for using QML methods to simulate quantum dynamics on near-term quantum hardware. We use generalization bounds, which bound the error a machine learning model makes on unseen data, to rigorously analyze the training data requirements of an algorithm within this framework. This provides a guarantee that our algorithm is resource-efficient, both in terms of qubit and data requirements. Our numerics exhibit efficient scaling with problem size, and we simulate 20 times longer than Trotterization on IBMQ-Bogota.

Out-of-distribution generalization for learning quantum dynamics

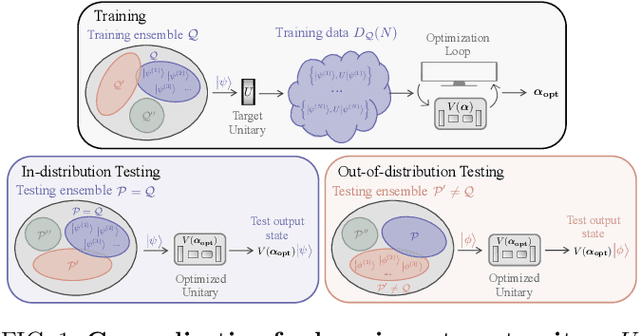
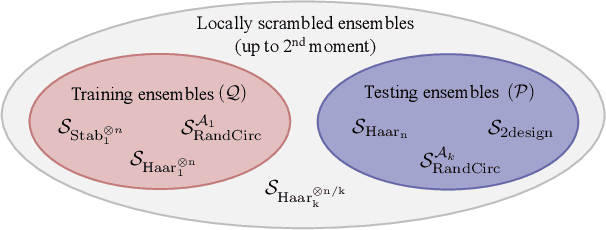
Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.