ClassiFIM: An Unsupervised Method To Detect Phase Transitions

Estimation of the Fisher Information Metric (FIM-estimation) is an important task that arises in unsupervised learning of phase transitions, a problem proposed by physicists. This work completes the definition of the task by defining rigorous evaluation metrics distMSE, distMSEPS, and distRE and introduces ClassiFIM, a novel machine learning method designed to solve the FIM-estimation task. Unlike existing methods for unsupervised learning of phase transitions, ClassiFIM directly estimates a well-defined quantity (the FIM), allowing it to be rigorously compared to any present and future other methods that estimate the same. ClassiFIM transforms a dataset for the FIM-estimation task into a dataset for an auxiliary binary classification task and involves selecting and training a model for the latter. We prove that the output of ClassiFIM approaches the exact FIM in the limit of infinite dataset size and under certain regularity conditions. We implement ClassiFIM on multiple datasets, including datasets describing classical and quantum phase transitions, and find that it achieves a good ground truth approximation with modest computational resources. Furthermore, we independently implement two alternative state-of-the-art methods for unsupervised estimation of phase transition locations on the same datasets and find that ClassiFIM predicts such locations at least as well as these other methods. To emphasize the generality of our method, we also propose and generate the MNIST-CNN dataset, which consists of the output of CNNs trained on MNIST for different hyperparameter choices. Using ClassiFIM on this dataset suggests there is a phase transition in the distribution of image-prediction pairs for CNNs trained on MNIST, demonstrating the broad scope of FIM-estimation beyond physics.

Quantum adiabatic machine learning with zooming

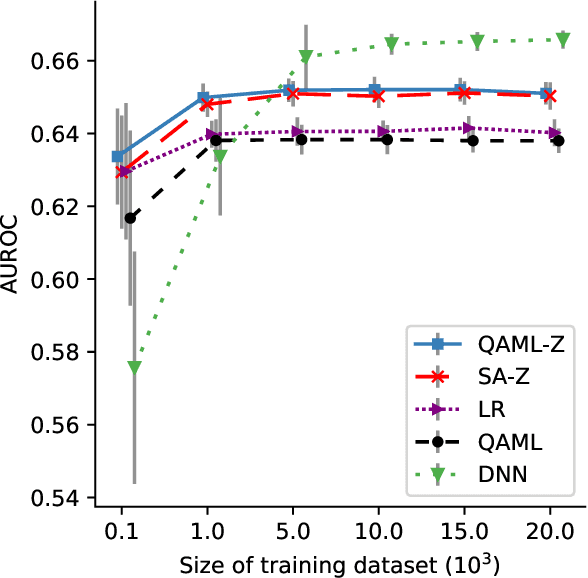
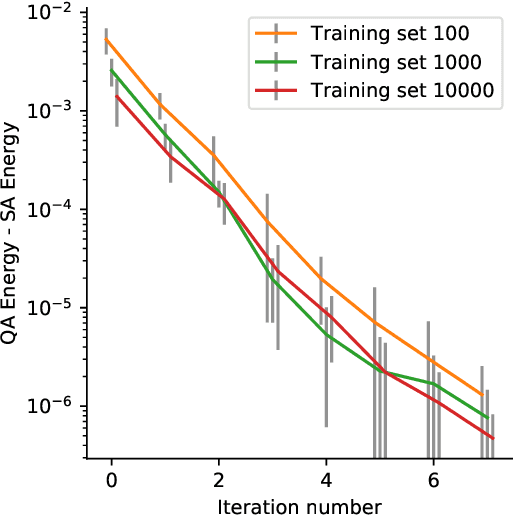
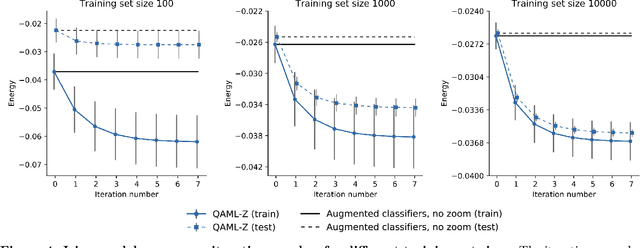
Recent work has shown that quantum annealing for machine learning (QAML) can perform comparably to state-of-the-art machine learning methods with a specific application to Higgs boson classification. We propose a variant algorithm (QAML-Z) that iteratively zooms in on a region of the energy surface by mapping the problem to a continuous space and sequentially applying quantum annealing to an augmented set of weak classifiers. Results on a programmable quantum annealer show that QAML-Z increases the performance difference between QAML and classical deep neural networks by over 40% as measured by area under the ROC curve for small training set sizes. Furthermore, QAML-Z reduces the advantage of deep neural networks over QAML for large training sets by around 50%, indicating that QAML-Z produces stronger classifiers that retain the robustness of the original QAML algorithm.

Charged particle tracking with quantum annealing-inspired optimization

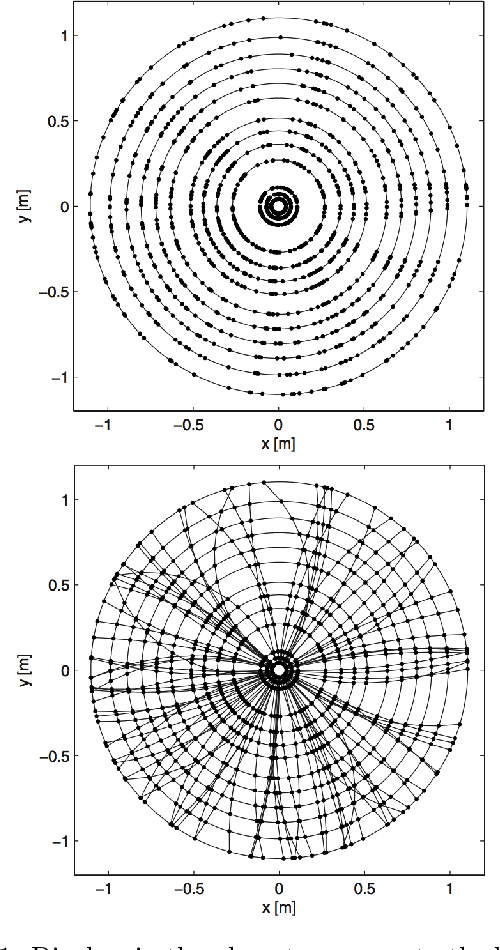
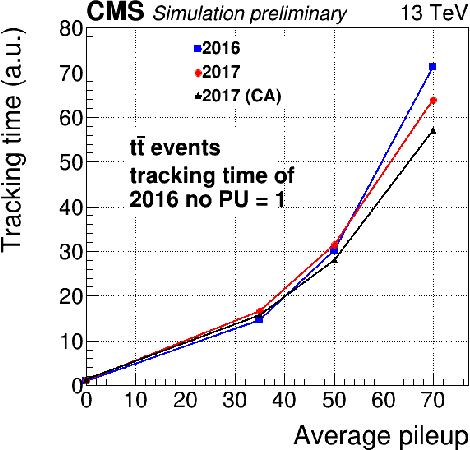
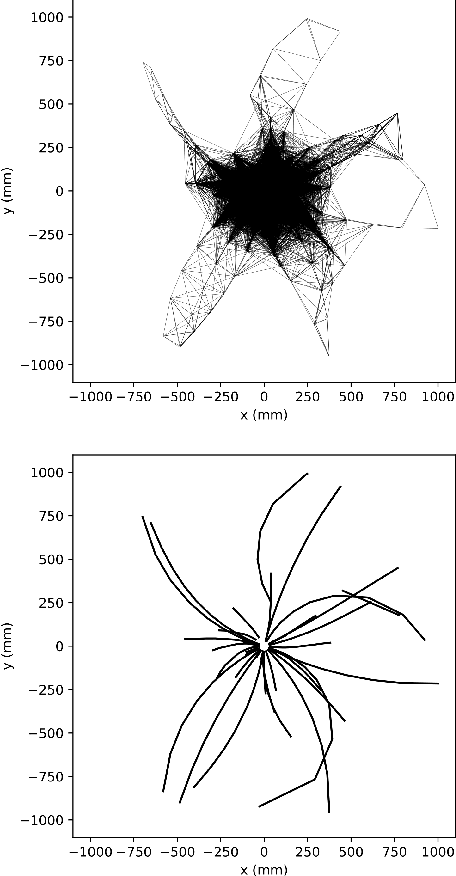
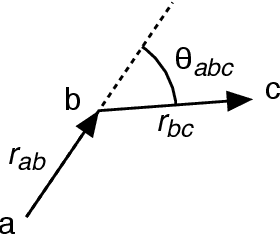
At the High Luminosity Large Hadron Collider (HL-LHC), traditional track reconstruction techniques that are critical for analysis are expected to face challenges due to scaling with track density. Quantum annealing has shown promise in its ability to solve combinatorial optimization problems amidst an ongoing effort to establish evidence of a quantum speedup. As a step towards exploiting such potential speedup, we investigate a track reconstruction approach by adapting the existing geometric Denby-Peterson (Hopfield) network method to the quantum annealing framework and to HL-LHC conditions. Furthermore, we develop additional techniques to embed the problem onto existing and near-term quantum annealing hardware. Results using simulated annealing and quantum annealing with the D-Wave 2X system on the TrackML dataset are presented, demonstrating the successful application of a quantum annealing-inspired algorithm to the track reconstruction challenge. We find that combinatorial optimization problems can effectively reconstruct tracks, suggesting possible applications for fast hardware-specific implementations at the LHC while leaving open the possibility of a quantum speedup for tracking.