Testing classical properties from quantum data

Many properties of Boolean functions can be tested far more efficiently than the function can be learned. However, this advantage often disappears when testers are limited to random samples--a natural setting for data science--rather than queries. In this work we investigate the quantum version of this scenario: quantum algorithms that test properties of a function $f$ solely from quantum data in the form of copies of the function state for $f$. For three well-established properties, we show that the speedup lost when restricting classical testers to samples can be recovered by testers that use quantum data. For monotonicity testing, we give a quantum algorithm that uses $\tilde{\mathcal{O}}(n^2)$ function state copies as compared to the $2^{\Omega(\sqrt{n})}$ samples required classically. We also present $\mathcal{O}(1)$-copy testers for symmetry and triangle-freeness, comparing favorably to classical lower bounds of $\Omega(n^{1/4})$ and $\Omega(n)$ samples respectively. These algorithms are time-efficient and necessarily include techniques beyond the Fourier sampling approaches applied to earlier testing problems. These results make the case for a general study of the advantages afforded by quantum data for testing. We contribute to this project by complementing our upper bounds with a lower bound of $\Omega(1/\varepsilon)$ for monotonicity testing from quantum data in the proximity regime $\varepsilon\leq\mathcal{O}(n^{-3/2})$. This implies a strict separation between testing monotonicity from quantum data and from quantum queries--where $\tilde{\mathcal{O}}(n)$ queries suffice when $\varepsilon=\Theta(n^{-3/2})$. We also exhibit a testing problem that can be solved from $\mathcal{O}(1)$ classical queries but requires $\Omega(2^{n/2})$ function state copies, complementing a separation of the same magnitude in the opposite direction derived from the Forrelation problem.

Interactive proofs for verifying (quantum) learning and testing

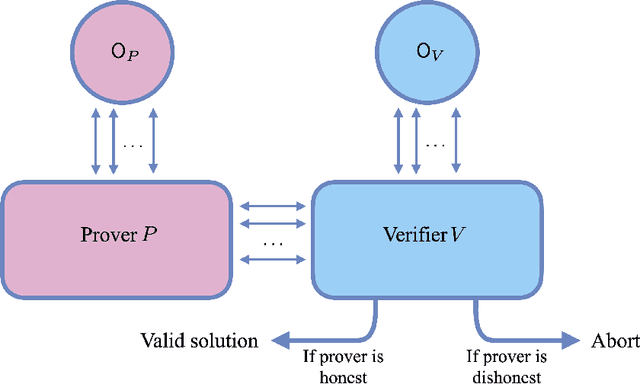
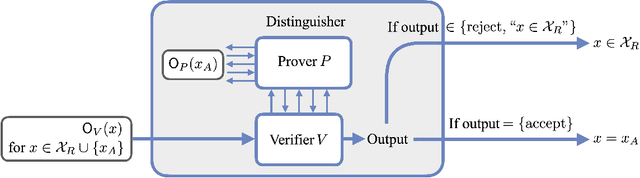
We consider the problem of testing and learning from data in the presence of resource constraints, such as limited memory or weak data access, which place limitations on the efficiency and feasibility of testing or learning. In particular, we ask the following question: Could a resource-constrained learner/tester use interaction with a resource-unconstrained but untrusted party to solve a learning or testing problem more efficiently than they could without such an interaction? In this work, we answer this question both abstractly and for concrete problems, in two complementary ways: For a wide variety of scenarios, we prove that a resource-constrained learner cannot gain any advantage through classical interaction with an untrusted prover. As a special case, we show that for the vast majority of testing and learning problems in which quantum memory is a meaningful resource, a memory-constrained quantum algorithm cannot overcome its limitations via classical communication with a memory-unconstrained quantum prover. In contrast, when quantum communication is allowed, we construct a variety of interactive proof protocols, for specific learning and testing problems, which allow memory-constrained quantum verifiers to gain significant advantages through delegation to untrusted provers. These results highlight both the limitations and potential of delegating learning and testing problems to resource-rich but untrusted third parties.

Online learning of quantum processes

Among recent insights into learning quantum states, online learning and shadow tomography procedures are notable for their ability to accurately predict expectation values even of adaptively chosen observables. In contrast to the state case, quantum process learning tasks with a similarly adaptive nature have received little attention. In this work, we investigate online learning tasks for quantum processes. Whereas online learning is infeasible for general quantum channels, we show that channels of bounded gate complexity as well as Pauli channels can be online learned in the regret and mistake-bounded models of online learning. In fact, we can online learn probabilistic mixtures of any exponentially large set of known channels. We also provide a provably sample-efficient shadow tomography procedure for Pauli channels. Our results extend beyond quantum channels to non-Markovian multi-time processes, with favorable regret and mistake bounds, as well as a shadow tomography procedure. We complement our online learning upper bounds with mistake as well as computational lower bounds. On the technical side, we make use of the multiplicative weights update algorithm, classical adaptive data analysis, and Bell sampling, as well as tools from the theory of quantum combs for multi-time quantum processes. Our work initiates a study of online learning for classes of quantum channels and, more generally, non-Markovian quantum processes. Given the importance of online learning for state shadow tomography, this may serve as a step towards quantum channel variants of adaptive shadow tomography.

Hamiltonian Property Testing

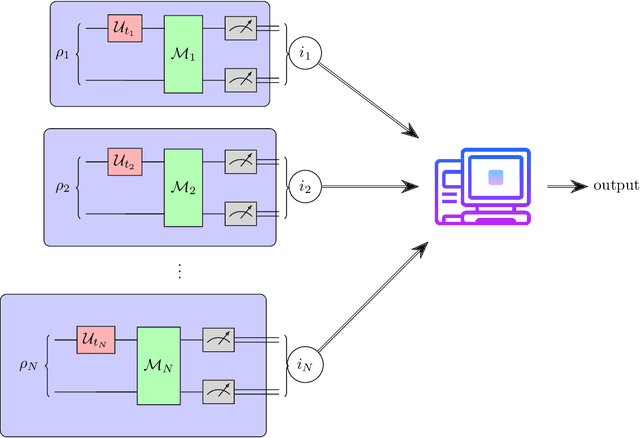
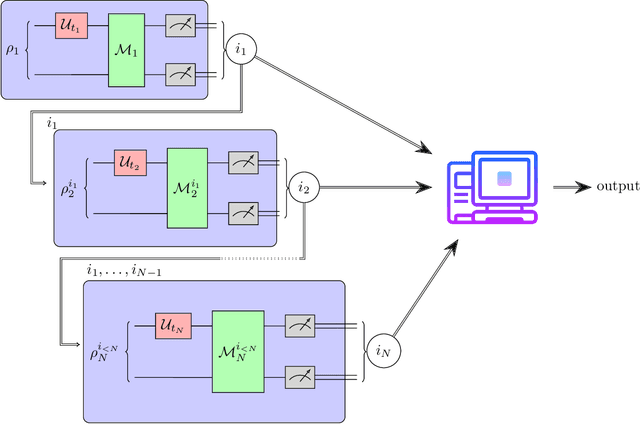
Locality is a fundamental feature of many physical time evolutions. Assumptions on locality and related structural properties also underlie recently proposed procedures for learning an unknown Hamiltonian from access to the induced time evolution. However, no protocols to rigorously test whether an unknown Hamiltonian is local were known. We investigate Hamiltonian locality testing as a property testing problem, where the task is to determine whether an unknown $n$-qubit Hamiltonian $H$ is $k$-local or $\varepsilon$-far from all $k$-local Hamiltonians, given access to the time evolution along $H$. First, we emphasize the importance of the chosen distance measure: With respect to the operator norm, a worst-case distance measure, incoherent quantum locality testers require $\tilde{\Omega}(2^n)$ many time evolution queries and an expected total evolution time of $\tilde{\Omega}(2^n / \varepsilon)$, and even coherent testers need $\Omega(2^{n/2})$ many queries and $\Omega(2^{n/2}/\varepsilon)$ total evolution time. In contrast, when distances are measured according to the normalized Frobenius norm, corresponding to an average-case distance, we give a sample-, time-, and computationally efficient incoherent Hamiltonian locality testing algorithm based on randomized measurements. In fact, our procedure can be used to simultaneously test a wide class of Hamiltonian properties beyond locality. Finally, we prove that learning a general Hamiltonian remains exponentially hard with this average-case distance, thereby establishing an exponential separation between Hamiltonian testing and learning. Our work initiates the study of property testing for quantum Hamiltonians, demonstrating that a broad class of Hamiltonian properties is efficiently testable even with limited quantum capabilities, and positioning Hamiltonian testing as an independent area of research alongside Hamiltonian learning.

Learning quantum states and unitaries of bounded gate complexity

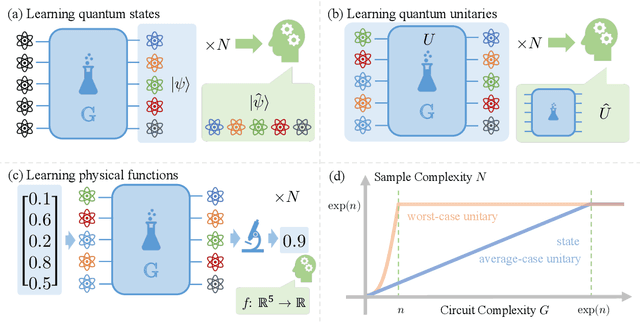
While quantum state tomography is notoriously hard, most states hold little interest to practically-minded tomographers. Given that states and unitaries appearing in Nature are of bounded gate complexity, it is natural to ask if efficient learning becomes possible. In this work, we prove that to learn a state generated by a quantum circuit with $G$ two-qubit gates to a small trace distance, a sample complexity scaling linearly in $G$ is necessary and sufficient. We also prove that the optimal query complexity to learn a unitary generated by $G$ gates to a small average-case error scales linearly in $G$. While sample-efficient learning can be achieved, we show that under reasonable cryptographic conjectures, the computational complexity for learning states and unitaries of gate complexity $G$ must scale exponentially in $G$. We illustrate how these results establish fundamental limitations on the expressivity of quantum machine learning models and provide new perspectives on no-free-lunch theorems in unitary learning. Together, our results answer how the complexity of learning quantum states and unitaries relate to the complexity of creating these states and unitaries.

Classical Verification of Quantum Learning

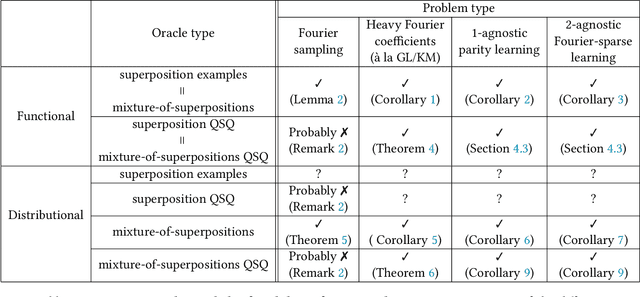
Quantum data access and quantum processing can make certain classically intractable learning tasks feasible. However, quantum capabilities will only be available to a select few in the near future. Thus, reliable schemes that allow classical clients to delegate learning to untrusted quantum servers are required to facilitate widespread access to quantum learning advantages. Building on a recently introduced framework of interactive proof systems for classical machine learning, we develop a framework for classical verification of quantum learning. We exhibit learning problems that a classical learner cannot efficiently solve on their own, but that they can efficiently and reliably solve when interacting with an untrusted quantum prover. Concretely, we consider the problems of agnostic learning parities and Fourier-sparse functions with respect to distributions with uniform input marginal. We propose a new quantum data access model that we call "mixture-of-superpositions" quantum examples, based on which we give efficient quantum learning algorithms for these tasks. Moreover, we prove that agnostic quantum parity and Fourier-sparse learning can be efficiently verified by a classical verifier with only random example or statistical query access. Finally, we showcase two general scenarios in learning and verification in which quantum mixture-of-superpositions examples do not lead to sample complexity improvements over classical data. Our results demonstrate that the potential power of quantum data for learning tasks, while not unlimited, can be utilized by classical agents through interaction with untrusted quantum entities.

The power and limitations of learning quantum dynamics incoherently

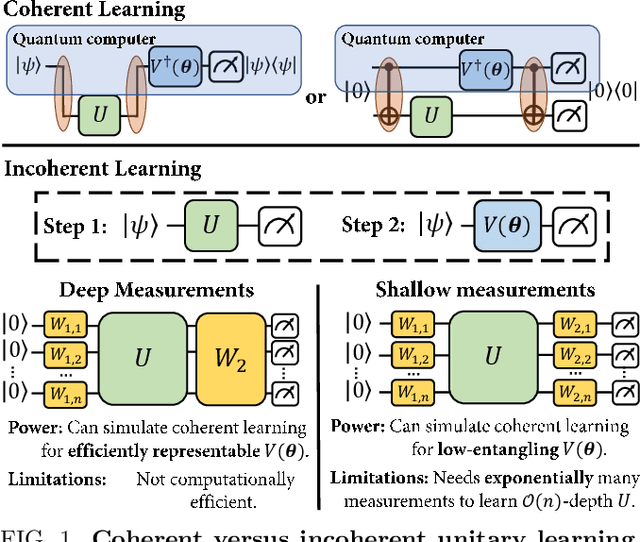
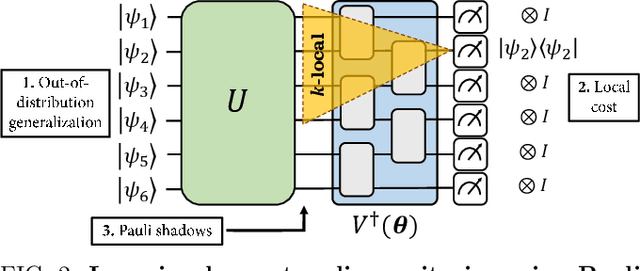
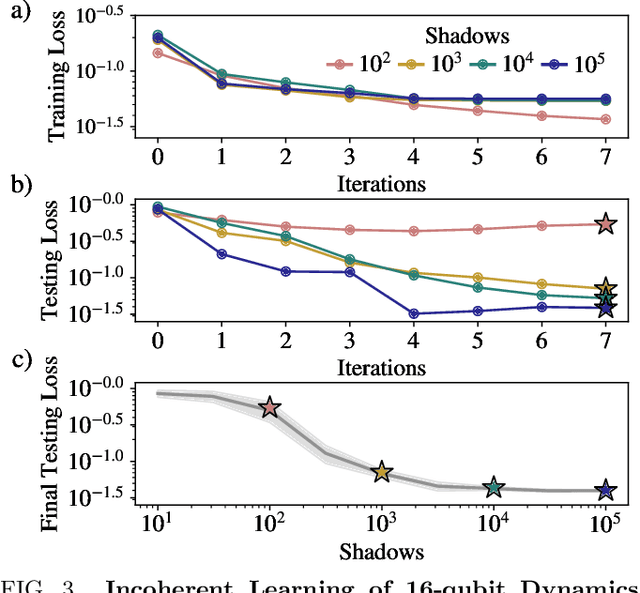
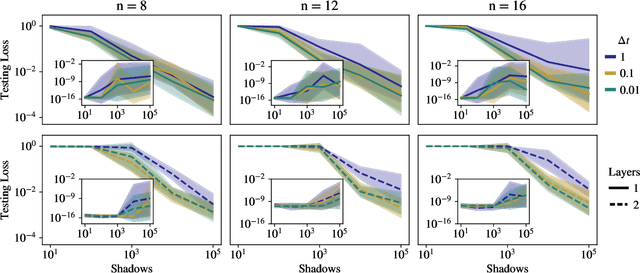
Quantum process learning is emerging as an important tool to study quantum systems. While studied extensively in coherent frameworks, where the target and model system can share quantum information, less attention has been paid to whether the dynamics of quantum systems can be learned without the system and target directly interacting. Such incoherent frameworks are practically appealing since they open up methods of transpiling quantum processes between the different physical platforms without the need for technically challenging hybrid entanglement schemes. Here we provide bounds on the sample complexity of learning unitary processes incoherently by analyzing the number of measurements that are required to emulate well-established coherent learning strategies. We prove that if arbitrary measurements are allowed, then any efficiently representable unitary can be efficiently learned within the incoherent framework; however, when restricted to shallow-depth measurements only low-entangling unitaries can be learned. We demonstrate our incoherent learning algorithm for low entangling unitaries by successfully learning a 16-qubit unitary on \texttt{ibmq\_kolkata}, and further demonstrate the scalabilty of our proposed algorithm through extensive numerical experiments.

Learning Quantum Processes and Hamiltonians via the Pauli Transfer Matrix

Learning about physical systems from quantum-enhanced experiments, relying on a quantum memory and quantum processing, can outperform learning from experiments in which only classical memory and processing are available. Whereas quantum advantages have been established for a variety of state learning tasks, quantum process learning allows for comparable advantages only with a careful problem formulation and is less understood. We establish an exponential quantum advantage for learning an unknown $n$-qubit quantum process $\mathcal{N}$. We show that a quantum memory allows to efficiently solve the following tasks: (a) learning the Pauli transfer matrix of an arbitrary $\mathcal{N}$, (b) predicting expectation values of bounded Pauli-sparse observables measured on the output of an arbitrary $\mathcal{N}$ upon input of a Pauli-sparse state, and (c) predicting expectation values of arbitrary bounded observables measured on the output of an unknown $\mathcal{N}$ with sparse Pauli transfer matrix upon input of an arbitrary state. With quantum memory, these tasks can be solved using linearly-in-$n$ many copies of the Choi state of $\mathcal{N}$, and even time-efficiently in the case of (b). In contrast, any learner without quantum memory requires exponentially-in-$n$ many queries, even when querying $\mathcal{N}$ on subsystems of adaptively chosen states and performing adaptively chosen measurements. In proving this separation, we extend existing shadow tomography upper and lower bounds from states to channels via the Choi-Jamiolkowski isomorphism. Moreover, we combine Pauli transfer matrix learning with polynomial interpolation techniques to develop a procedure for learning arbitrary Hamiltonians, which may have non-local all-to-all interactions, from short-time dynamics. Our results highlight the power of quantum-enhanced experiments for learning highly complex quantum dynamics.

Dynamical simulation via quantum machine learning with provable generalization

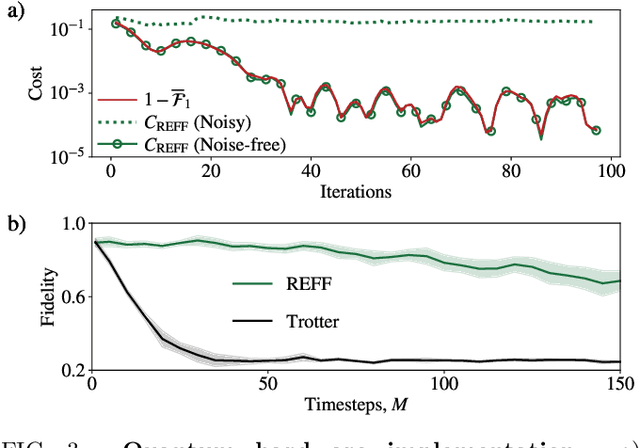
Much attention has been paid to dynamical simulation and quantum machine learning (QML) independently as applications for quantum advantage, while the possibility of using QML to enhance dynamical simulations has not been thoroughly investigated. Here we develop a framework for using QML methods to simulate quantum dynamics on near-term quantum hardware. We use generalization bounds, which bound the error a machine learning model makes on unseen data, to rigorously analyze the training data requirements of an algorithm within this framework. This provides a guarantee that our algorithm is resource-efficient, both in terms of qubit and data requirements. Our numerics exhibit efficient scaling with problem size, and we simulate 20 times longer than Trotterization on IBMQ-Bogota.

Out-of-distribution generalization for learning quantum dynamics

Generalization bounds are a critical tool to assess the training data requirements of Quantum Machine Learning (QML). Recent work has established guarantees for in-distribution generalization of quantum neural networks (QNNs), where training and testing data are assumed to be drawn from the same data distribution. However, there are currently no results on out-of-distribution generalization in QML, where we require a trained model to perform well even on data drawn from a distribution different from the training distribution. In this work, we prove out-of-distribution generalization for the task of learning an unknown unitary using a QNN and for a broad class of training and testing distributions. In particular, we show that one can learn the action of a unitary on entangled states using only product state training data. We numerically illustrate this by showing that the evolution of a Heisenberg spin chain can be learned using only product training states. Since product states can be prepared using only single-qubit gates, this advances the prospects of learning quantum dynamics using near term quantum computers and quantum experiments, and further opens up new methods for both the classical and quantum compilation of quantum circuits.