Hamiltonian Property Testing
Paper and Code
Mar 05, 2024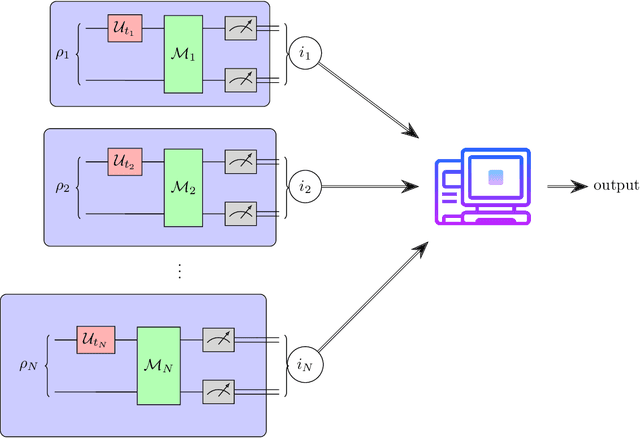
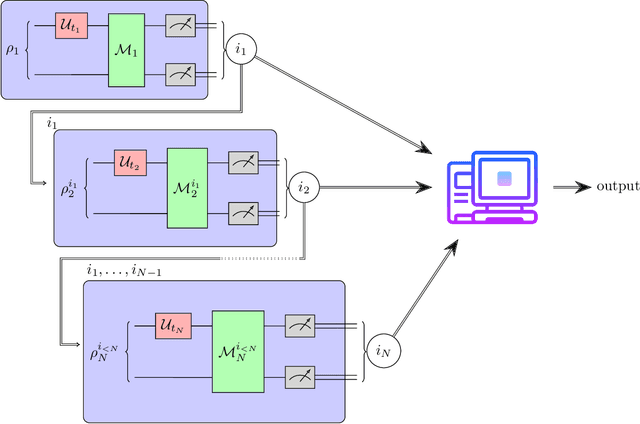

Locality is a fundamental feature of many physical time evolutions. Assumptions on locality and related structural properties also underlie recently proposed procedures for learning an unknown Hamiltonian from access to the induced time evolution. However, no protocols to rigorously test whether an unknown Hamiltonian is local were known. We investigate Hamiltonian locality testing as a property testing problem, where the task is to determine whether an unknown $n$-qubit Hamiltonian $H$ is $k$-local or $\varepsilon$-far from all $k$-local Hamiltonians, given access to the time evolution along $H$. First, we emphasize the importance of the chosen distance measure: With respect to the operator norm, a worst-case distance measure, incoherent quantum locality testers require $\tilde{\Omega}(2^n)$ many time evolution queries and an expected total evolution time of $\tilde{\Omega}(2^n / \varepsilon)$, and even coherent testers need $\Omega(2^{n/2})$ many queries and $\Omega(2^{n/2}/\varepsilon)$ total evolution time. In contrast, when distances are measured according to the normalized Frobenius norm, corresponding to an average-case distance, we give a sample-, time-, and computationally efficient incoherent Hamiltonian locality testing algorithm based on randomized measurements. In fact, our procedure can be used to simultaneously test a wide class of Hamiltonian properties beyond locality. Finally, we prove that learning a general Hamiltonian remains exponentially hard with this average-case distance, thereby establishing an exponential separation between Hamiltonian testing and learning. Our work initiates the study of property testing for quantum Hamiltonians, demonstrating that a broad class of Hamiltonian properties is efficiently testable even with limited quantum capabilities, and positioning Hamiltonian testing as an independent area of research alongside Hamiltonian learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge