Learning quantum states and unitaries of bounded gate complexity

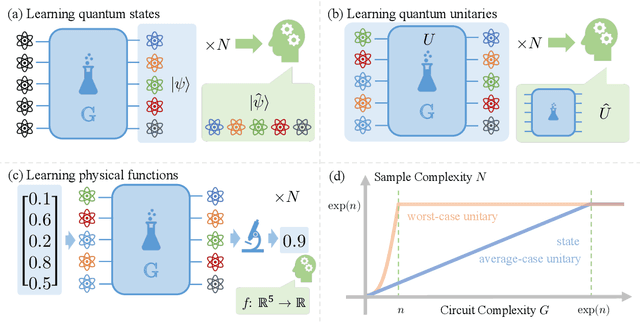
While quantum state tomography is notoriously hard, most states hold little interest to practically-minded tomographers. Given that states and unitaries appearing in Nature are of bounded gate complexity, it is natural to ask if efficient learning becomes possible. In this work, we prove that to learn a state generated by a quantum circuit with $G$ two-qubit gates to a small trace distance, a sample complexity scaling linearly in $G$ is necessary and sufficient. We also prove that the optimal query complexity to learn a unitary generated by $G$ gates to a small average-case error scales linearly in $G$. While sample-efficient learning can be achieved, we show that under reasonable cryptographic conjectures, the computational complexity for learning states and unitaries of gate complexity $G$ must scale exponentially in $G$. We illustrate how these results establish fundamental limitations on the expressivity of quantum machine learning models and provide new perspectives on no-free-lunch theorems in unitary learning. Together, our results answer how the complexity of learning quantum states and unitaries relate to the complexity of creating these states and unitaries.

A single $T$-gate makes distribution learning hard

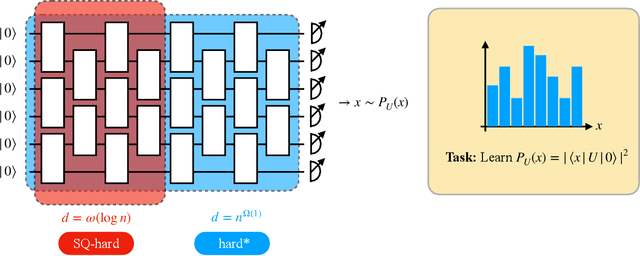
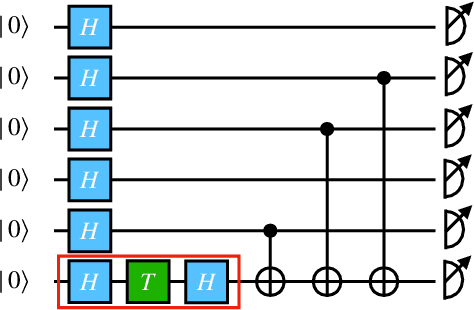
The task of learning a probability distribution from samples is ubiquitous across the natural sciences. The output distributions of local quantum circuits form a particularly interesting class of distributions, of key importance both to quantum advantage proposals and a variety of quantum machine learning algorithms. In this work, we provide an extensive characterization of the learnability of the output distributions of local quantum circuits. Our first result yields insight into the relationship between the efficient learnability and the efficient simulatability of these distributions. Specifically, we prove that the density modelling problem associated with Clifford circuits can be efficiently solved, while for depth $d=n^{\Omega(1)}$ circuits the injection of a single $T$-gate into the circuit renders this problem hard. This result shows that efficient simulatability does not imply efficient learnability. Our second set of results provides insight into the potential and limitations of quantum generative modelling algorithms. We first show that the generative modelling problem associated with depth $d=n^{\Omega(1)}$ local quantum circuits is hard for any learning algorithm, classical or quantum. As a consequence, one cannot use a quantum algorithm to gain a practical advantage for this task. We then show that, for a wide variety of the most practically relevant learning algorithms -- including hybrid-quantum classical algorithms -- even the generative modelling problem associated with depth $d=\omega(\log(n))$ Clifford circuits is hard. This result places limitations on the applicability of near-term hybrid quantum-classical generative modelling algorithms.

Learnability of the output distributions of local quantum circuits

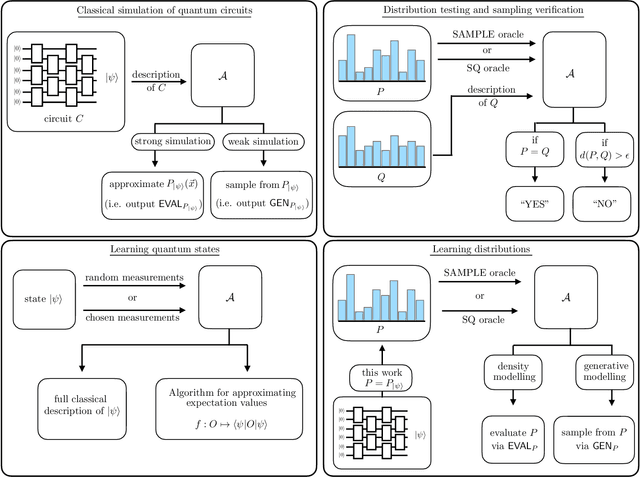
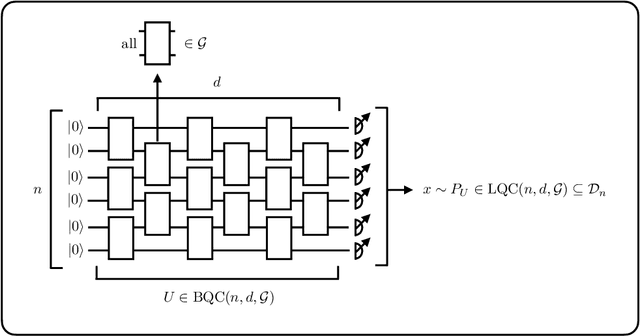
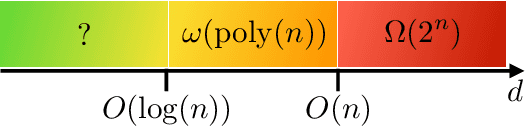
There is currently a large interest in understanding the potential advantages quantum devices can offer for probabilistic modelling. In this work we investigate, within two different oracle models, the probably approximately correct (PAC) learnability of quantum circuit Born machines, i.e., the output distributions of local quantum circuits. We first show a negative result, namely, that the output distributions of super-logarithmic depth Clifford circuits are not sample-efficiently learnable in the statistical query model, i.e., when given query access to empirical expectation values of bounded functions over the sample space. This immediately implies the hardness, for both quantum and classical algorithms, of learning from statistical queries the output distributions of local quantum circuits using any gate set which includes the Clifford group. As many practical generative modelling algorithms use statistical queries -- including those for training quantum circuit Born machines -- our result is broadly applicable and strongly limits the possibility of a meaningful quantum advantage for learning the output distributions of local quantum circuits. As a positive result, we show that in a more powerful oracle model, namely when directly given access to samples, the output distributions of local Clifford circuits are computationally efficiently PAC learnable by a classical learner. Our results are equally applicable to the problems of learning an algorithm for generating samples from the target distribution (generative modelling) and learning an algorithm for evaluating its probabilities (density modelling). They provide the first rigorous insights into the learnability of output distributions of local quantum circuits from the probabilistic modelling perspective.

Private learning implies quantum stability

Learning an unknown $n$-qubit quantum state $\rho$ is a fundamental challenge in quantum computing. Information-theoretically, it is known that tomography requires exponential in $n$ many copies of $\rho$ to estimate it up to trace distance. Motivated by computational learning theory, Aaronson et al. introduced many (weaker) learning models: the PAC model of learning states (Proceedings of Royal Society A'07), shadow tomography (STOC'18) for learning "shadows" of a state, a model that also requires learners to be differentially private (STOC'19) and the online model of learning states (NeurIPS'18). In these models it was shown that an unknown state can be learned "approximately" using linear-in-$n$ many copies of rho. But is there any relationship between these models? In this paper we prove a sequence of (information-theoretic) implications from differentially-private PAC learning, to communication complexity, to online learning and then to quantum stability. Our main result generalizes the recent work of Bun, Livni and Moran (Journal of the ACM'21) who showed that finite Littlestone dimension (of Boolean-valued concept classes) implies PAC learnability in the (approximate) differentially private (DP) setting. We first consider their work in the real-valued setting and further extend their techniques to the setting of learning quantum states. Key to our results is our generic quantum online learner, Robust Standard Optimal Algorithm (RSOA), which is robust to adversarial imprecision. We then show information-theoretic implications between DP learning quantum states in the PAC model, learnability of quantum states in the one-way communication model, online learning of quantum states, quantum stability (which is our conceptual contribution), various combinatorial parameters and give further applications to gentle shadow tomography and noisy quantum state learning.

Robust quantum minimum finding with an application to hypothesis selection

We consider the problem of finding the minimum element in a list of length $N$ using a noisy comparator. The noise is modelled as follows: given two elements to compare, if the values of the elements differ by at least $\alpha$ by some metric defined on the elements, then the comparison will be made correctly; if the values of the elements are closer than $\alpha$, the outcome of the comparison is not subject to any guarantees. We demonstrate a quantum algorithm for noisy quantum minimum-finding that preserves the quadratic speedup of the noiseless case: our algorithm runs in time $\tilde O(\sqrt{N (1+\Delta)})$, where $\Delta$ is an upper-bound on the number of elements within the interval $\alpha$, and outputs a good approximation of the true minimum with high probability. Our noisy comparator model is motivated by the problem of hypothesis selection, where given a set of $N$ known candidate probability distributions and samples from an unknown target distribution, one seeks to output some candidate distribution $O(\varepsilon)$-close to the unknown target. Much work on the classical front has been devoted to speeding up the run time of classical hypothesis selection from $O(N^2)$ to $O(N)$, in part by using statistical primitives such as the Scheff\'{e} test. Assuming a quantum oracle generalization of the classical data access and applying our noisy quantum minimum-finding algorithm, we take this run time into the sublinear regime. The final expected run time is $\tilde O( \sqrt{N(1+\Delta)})$, with the same $O(\log N)$ sample complexity from the unknown distribution as the classical algorithm. We expect robust quantum minimum-finding to be a useful building block for algorithms in situations where the comparator (which may be another quantum or classical algorithm) is resolution-limited or subject to some uncertainty.

Adaptive Quantum State Tomography with Neural Networks

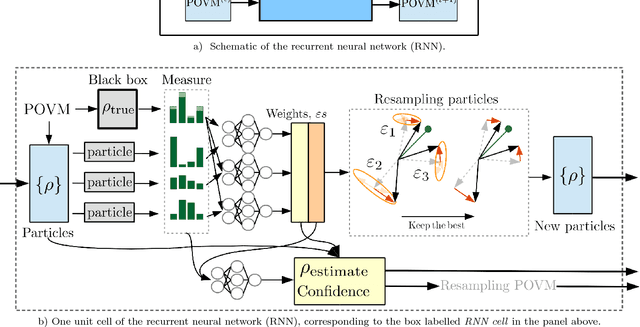
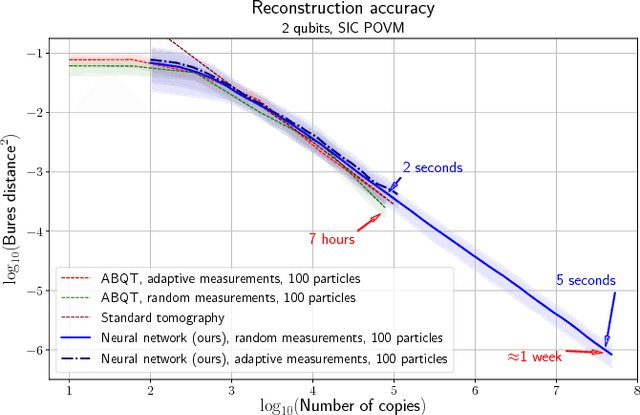
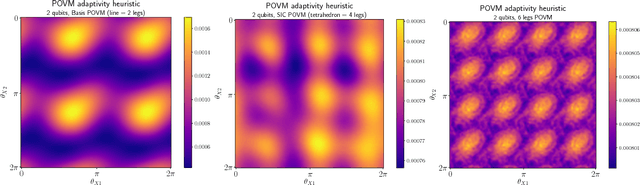
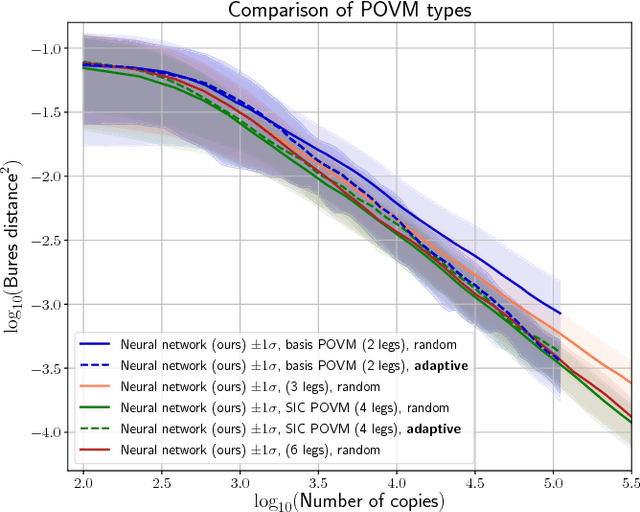
Quantum State Tomography is the task of determining an unknown quantum state by making measurements on identical copies of the state. Current algorithms are costly both on the experimental front -- requiring vast numbers of measurements -- as well as in terms of the computational time to analyze those measurements. In this paper, we address the problem of analysis speed and flexibility, introducing \textit{Neural Adaptive Quantum State Tomography} (NA-QST), a machine learning based algorithm for quantum state tomography that adapts measurements and provides orders of magnitude faster processing while retaining state-of-the-art reconstruction accuracy. Our algorithm is inspired by particle swarm optimization and Bayesian particle-filter based adaptive methods, which we extend and enhance using neural networks. The resampling step, in which a bank of candidate solutions -- particles -- is refined, is in our case learned directly from data, removing the computational bottleneck of standard methods. We successfully replace the Bayesian calculation that requires computational time of $O(\mathrm{poly}(n))$ with a learned heuristic whose time complexity empirically scales as $O(\log(n))$ with the number of copies measured $n$, while retaining the same reconstruction accuracy. This corresponds to a factor of a million speedup for $10^7$ copies measured. We demonstrate that our algorithm learns to work with basis, symmetric informationally complete (SIC), as well as other types of POVMs. We discuss the value of measurement adaptivity for each POVM type, demonstrating that its effect is significant only for basis POVMs. Our algorithm can be retrained within hours on a single laptop for a two-qubit situation, which suggests a feasible time-cost when extended to larger systems. It can also adapt to a subset of possible states, a choice of the type of measurement, and other experimental details.