A super-polynomial quantum-classical separation for density modelling

Density modelling is the task of learning an unknown probability density function from samples, and is one of the central problems of unsupervised machine learning. In this work, we show that there exists a density modelling problem for which fault-tolerant quantum computers can offer a super-polynomial advantage over classical learning algorithms, given standard cryptographic assumptions. Along the way, we provide a variety of additional results and insights, of potential interest for proving future distribution learning separations between quantum and classical learning algorithms. Specifically, we (a) provide an overview of the relationships between hardness results in supervised learning and distribution learning, and (b) show that any weak pseudo-random function can be used to construct a classically hard density modelling problem. The latter result opens up the possibility of proving quantum-classical separations for density modelling based on weaker assumptions than those necessary for pseudo-random functions.

A single $T$-gate makes distribution learning hard

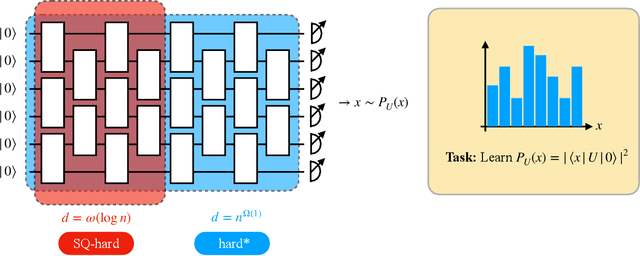
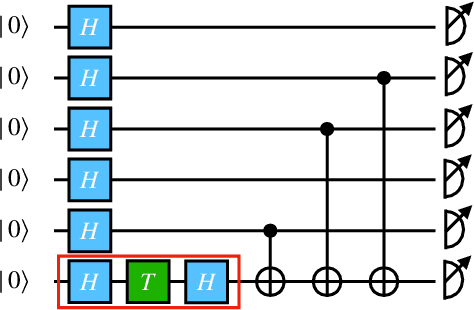
The task of learning a probability distribution from samples is ubiquitous across the natural sciences. The output distributions of local quantum circuits form a particularly interesting class of distributions, of key importance both to quantum advantage proposals and a variety of quantum machine learning algorithms. In this work, we provide an extensive characterization of the learnability of the output distributions of local quantum circuits. Our first result yields insight into the relationship between the efficient learnability and the efficient simulatability of these distributions. Specifically, we prove that the density modelling problem associated with Clifford circuits can be efficiently solved, while for depth $d=n^{\Omega(1)}$ circuits the injection of a single $T$-gate into the circuit renders this problem hard. This result shows that efficient simulatability does not imply efficient learnability. Our second set of results provides insight into the potential and limitations of quantum generative modelling algorithms. We first show that the generative modelling problem associated with depth $d=n^{\Omega(1)}$ local quantum circuits is hard for any learning algorithm, classical or quantum. As a consequence, one cannot use a quantum algorithm to gain a practical advantage for this task. We then show that, for a wide variety of the most practically relevant learning algorithms -- including hybrid-quantum classical algorithms -- even the generative modelling problem associated with depth $d=\omega(\log(n))$ Clifford circuits is hard. This result places limitations on the applicability of near-term hybrid quantum-classical generative modelling algorithms.

Learnability of the output distributions of local quantum circuits

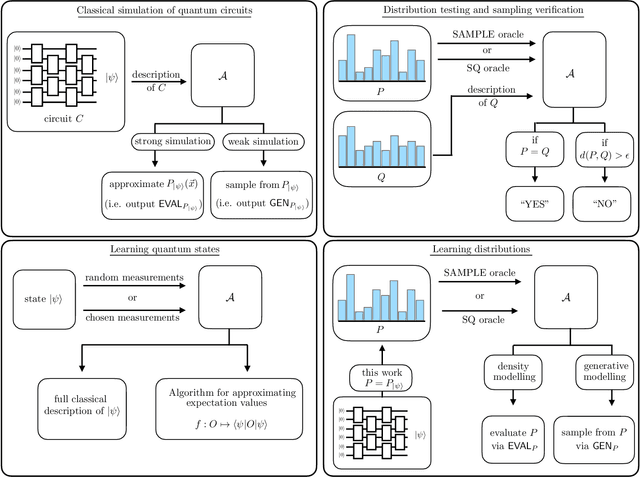
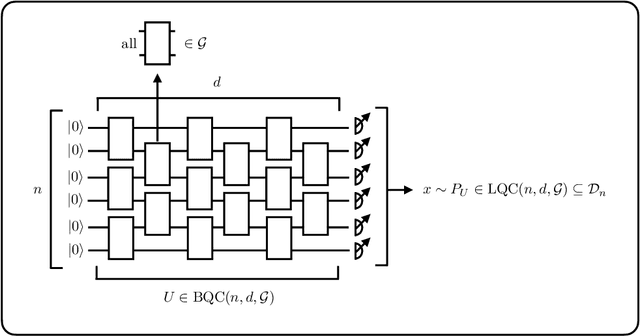
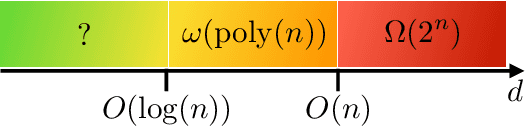
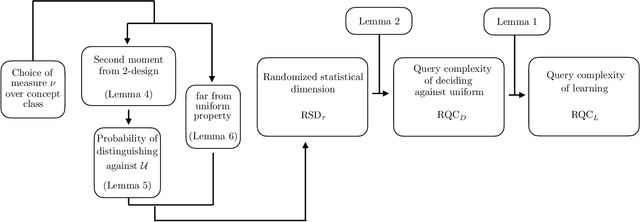
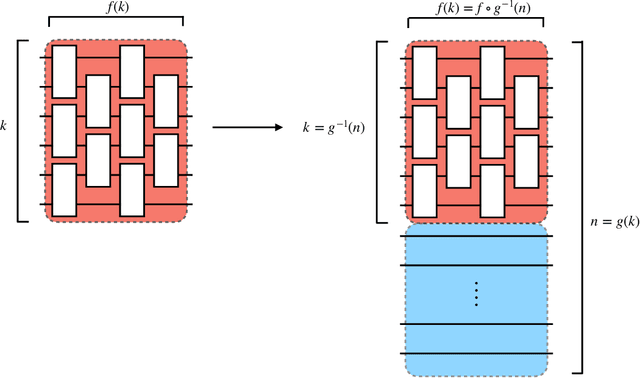
There is currently a large interest in understanding the potential advantages quantum devices can offer for probabilistic modelling. In this work we investigate, within two different oracle models, the probably approximately correct (PAC) learnability of quantum circuit Born machines, i.e., the output distributions of local quantum circuits. We first show a negative result, namely, that the output distributions of super-logarithmic depth Clifford circuits are not sample-efficiently learnable in the statistical query model, i.e., when given query access to empirical expectation values of bounded functions over the sample space. This immediately implies the hardness, for both quantum and classical algorithms, of learning from statistical queries the output distributions of local quantum circuits using any gate set which includes the Clifford group. As many practical generative modelling algorithms use statistical queries -- including those for training quantum circuit Born machines -- our result is broadly applicable and strongly limits the possibility of a meaningful quantum advantage for learning the output distributions of local quantum circuits. As a positive result, we show that in a more powerful oracle model, namely when directly given access to samples, the output distributions of local Clifford circuits are computationally efficiently PAC learnable by a classical learner. Our results are equally applicable to the problems of learning an algorithm for generating samples from the target distribution (generative modelling) and learning an algorithm for evaluating its probabilities (density modelling). They provide the first rigorous insights into the learnability of output distributions of local quantum circuits from the probabilistic modelling perspective.

On the Quantum versus Classical Learnability of Discrete Distributions

Here we study the comparative power of classical and quantum learners for generative modelling within the Probably Approximately Correct (PAC) framework. More specifically we consider the following task: Given samples from some unknown discrete probability distribution, output with high probability an efficient algorithm for generating new samples from a good approximation of the original distribution. Our primary result is the explicit construction of a class of discrete probability distributions which, under the decisional Diffie-Hellman assumption, is provably not efficiently PAC learnable by a classical generative modelling algorithm, but for which we construct an efficient quantum learner. This class of distributions therefore provides a concrete example of a generative modelling problem for which quantum learners exhibit a provable advantage over classical learning algorithms. In addition, we discuss techniques for proving classical generative modelling hardness results, as well as the relationship between the PAC learnability of Boolean functions and the PAC learnability of discrete probability distributions.