Interactive proofs for verifying (quantum) learning and testing

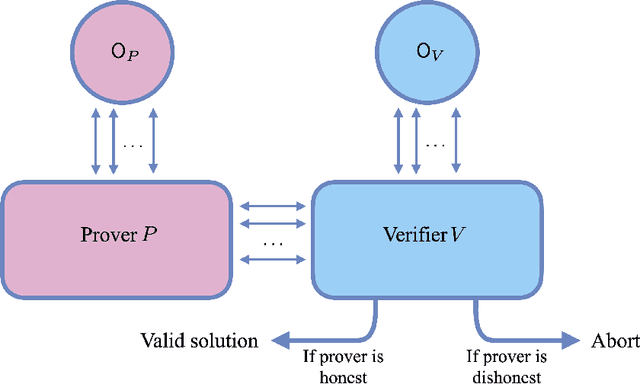
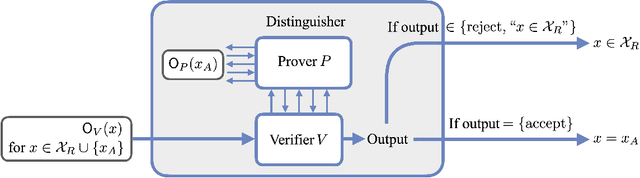
We consider the problem of testing and learning from data in the presence of resource constraints, such as limited memory or weak data access, which place limitations on the efficiency and feasibility of testing or learning. In particular, we ask the following question: Could a resource-constrained learner/tester use interaction with a resource-unconstrained but untrusted party to solve a learning or testing problem more efficiently than they could without such an interaction? In this work, we answer this question both abstractly and for concrete problems, in two complementary ways: For a wide variety of scenarios, we prove that a resource-constrained learner cannot gain any advantage through classical interaction with an untrusted prover. As a special case, we show that for the vast majority of testing and learning problems in which quantum memory is a meaningful resource, a memory-constrained quantum algorithm cannot overcome its limitations via classical communication with a memory-unconstrained quantum prover. In contrast, when quantum communication is allowed, we construct a variety of interactive proof protocols, for specific learning and testing problems, which allow memory-constrained quantum verifiers to gain significant advantages through delegation to untrusted provers. These results highlight both the limitations and potential of delegating learning and testing problems to resource-rich but untrusted third parties.

Classical Verification of Quantum Learning

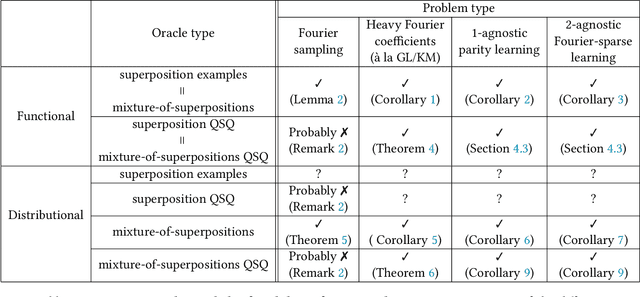
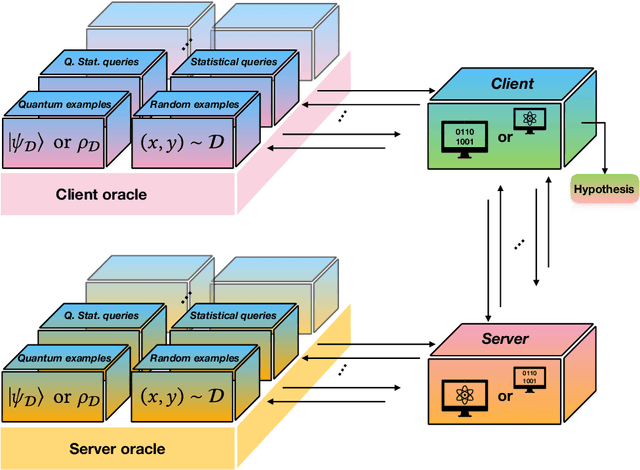
Quantum data access and quantum processing can make certain classically intractable learning tasks feasible. However, quantum capabilities will only be available to a select few in the near future. Thus, reliable schemes that allow classical clients to delegate learning to untrusted quantum servers are required to facilitate widespread access to quantum learning advantages. Building on a recently introduced framework of interactive proof systems for classical machine learning, we develop a framework for classical verification of quantum learning. We exhibit learning problems that a classical learner cannot efficiently solve on their own, but that they can efficiently and reliably solve when interacting with an untrusted quantum prover. Concretely, we consider the problems of agnostic learning parities and Fourier-sparse functions with respect to distributions with uniform input marginal. We propose a new quantum data access model that we call "mixture-of-superpositions" quantum examples, based on which we give efficient quantum learning algorithms for these tasks. Moreover, we prove that agnostic quantum parity and Fourier-sparse learning can be efficiently verified by a classical verifier with only random example or statistical query access. Finally, we showcase two general scenarios in learning and verification in which quantum mixture-of-superpositions examples do not lead to sample complexity improvements over classical data. Our results demonstrate that the potential power of quantum data for learning tasks, while not unlimited, can be utilized by classical agents through interaction with untrusted quantum entities.

On the average-case complexity of learning output distributions of quantum circuits

In this work, we show that learning the output distributions of brickwork random quantum circuits is average-case hard in the statistical query model. This learning model is widely used as an abstract computational model for most generic learning algorithms. In particular, for brickwork random quantum circuits on $n$ qubits of depth $d$, we show three main results: - At super logarithmic circuit depth $d=\omega(\log(n))$, any learning algorithm requires super polynomially many queries to achieve a constant probability of success over the randomly drawn instance. - There exists a $d=O(n)$, such that any learning algorithm requires $\Omega(2^n)$ queries to achieve a $O(2^{-n})$ probability of success over the randomly drawn instance. - At infinite circuit depth $d\to\infty$, any learning algorithm requires $2^{2^{\Omega(n)}}$ many queries to achieve a $2^{-2^{\Omega(n)}}$ probability of success over the randomly drawn instance. As an auxiliary result of independent interest, we show that the output distribution of a brickwork random quantum circuit is constantly far from any fixed distribution in total variation distance with probability $1-O(2^{-n})$, which confirms a variant of a conjecture by Aaronson and Chen.

A single $T$-gate makes distribution learning hard

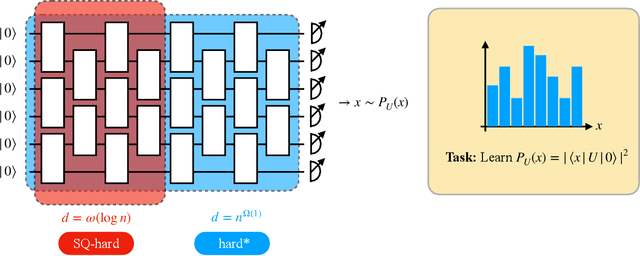
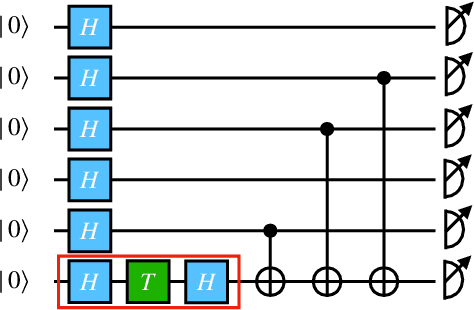
The task of learning a probability distribution from samples is ubiquitous across the natural sciences. The output distributions of local quantum circuits form a particularly interesting class of distributions, of key importance both to quantum advantage proposals and a variety of quantum machine learning algorithms. In this work, we provide an extensive characterization of the learnability of the output distributions of local quantum circuits. Our first result yields insight into the relationship between the efficient learnability and the efficient simulatability of these distributions. Specifically, we prove that the density modelling problem associated with Clifford circuits can be efficiently solved, while for depth $d=n^{\Omega(1)}$ circuits the injection of a single $T$-gate into the circuit renders this problem hard. This result shows that efficient simulatability does not imply efficient learnability. Our second set of results provides insight into the potential and limitations of quantum generative modelling algorithms. We first show that the generative modelling problem associated with depth $d=n^{\Omega(1)}$ local quantum circuits is hard for any learning algorithm, classical or quantum. As a consequence, one cannot use a quantum algorithm to gain a practical advantage for this task. We then show that, for a wide variety of the most practically relevant learning algorithms -- including hybrid-quantum classical algorithms -- even the generative modelling problem associated with depth $d=\omega(\log(n))$ Clifford circuits is hard. This result places limitations on the applicability of near-term hybrid quantum-classical generative modelling algorithms.

Learnability of the output distributions of local quantum circuits

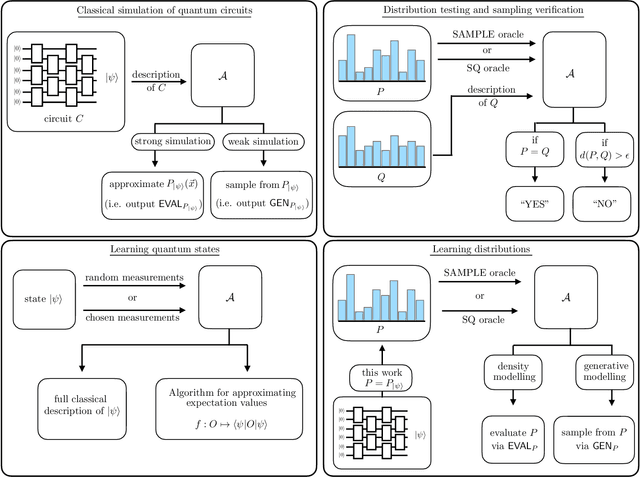
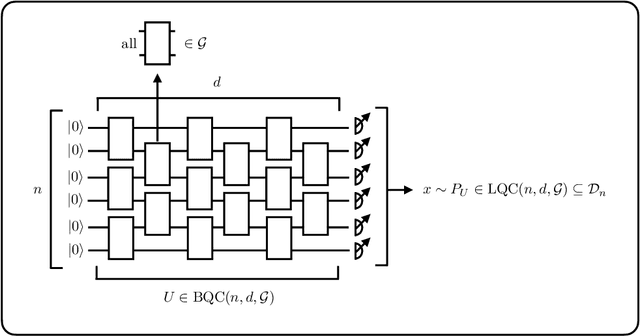
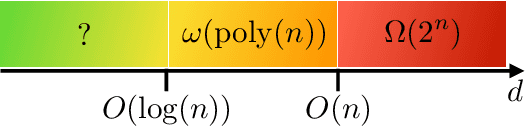
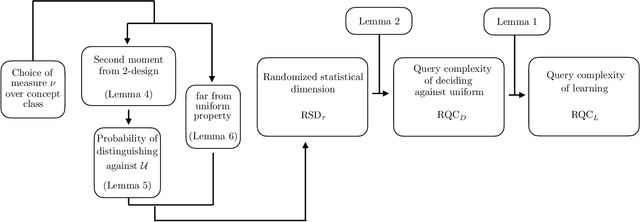
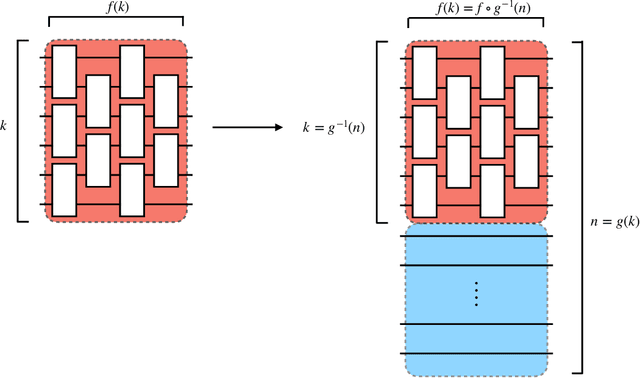
There is currently a large interest in understanding the potential advantages quantum devices can offer for probabilistic modelling. In this work we investigate, within two different oracle models, the probably approximately correct (PAC) learnability of quantum circuit Born machines, i.e., the output distributions of local quantum circuits. We first show a negative result, namely, that the output distributions of super-logarithmic depth Clifford circuits are not sample-efficiently learnable in the statistical query model, i.e., when given query access to empirical expectation values of bounded functions over the sample space. This immediately implies the hardness, for both quantum and classical algorithms, of learning from statistical queries the output distributions of local quantum circuits using any gate set which includes the Clifford group. As many practical generative modelling algorithms use statistical queries -- including those for training quantum circuit Born machines -- our result is broadly applicable and strongly limits the possibility of a meaningful quantum advantage for learning the output distributions of local quantum circuits. As a positive result, we show that in a more powerful oracle model, namely when directly given access to samples, the output distributions of local Clifford circuits are computationally efficiently PAC learnable by a classical learner. Our results are equally applicable to the problems of learning an algorithm for generating samples from the target distribution (generative modelling) and learning an algorithm for evaluating its probabilities (density modelling). They provide the first rigorous insights into the learnability of output distributions of local quantum circuits from the probabilistic modelling perspective.