Information-Computation Gaps in Quantum Learning via Low-Degree Likelihood

In a variety of physically relevant settings for learning from quantum data, designing protocols that can computationally efficiently extract information remains largely an art, and there are important cases where we believe this to be impossible, that is, where there is an information-computation gap. While there is a large array of tools in the classical literature for giving evidence for average-case hardness of statistical inference problems, the corresponding tools in the quantum literature are far more limited. One such framework in the classical literature, the low-degree method, makes predictions about hardness of inference problems based on the failure of estimators given by low-degree polynomials. In this work, we extend this framework to the quantum setting. We establish a general connection between state designs and low-degree hardness. We use this to obtain the first information-computation gaps for learning Gibbs states of random, sparse, non-local Hamiltonians. We also use it to prove hardness for learning random shallow quantum circuit states in a challenging model where states can be measured in adaptively chosen bases. To our knowledge, the ability to model adaptivity within the low-degree framework was open even in classical settings. In addition, we also obtain a low-degree hardness result for quantum error mitigation against strategies with single-qubit measurements. We define a new quantum generalization of the planted biclique problem and identify the threshold at which this problem becomes computationally hard for protocols that perform local measurements. Interestingly, the complexity landscape for this problem shifts when going from local measurements to more entangled single-copy measurements. We show average-case hardness for the "standard" variant of Learning Stabilizers with Noise and for agnostically learning product states.

On the sample complexity of purity and inner product estimation

We study the sample complexity of the prototypical tasks quantum purity estimation and quantum inner product estimation. In purity estimation, we are to estimate $tr(\rho^2)$ of an unknown quantum state $\rho$ to additive error $\epsilon$. Meanwhile, for quantum inner product estimation, Alice and Bob are to estimate $tr(\rho\sigma)$ to additive error $\epsilon$ given copies of unknown quantum state $\rho$ and $\sigma$ using classical communication and restricted quantum communication. In this paper, we show a strong connection between the sample complexity of purity estimation with bounded quantum memory and inner product estimation with bounded quantum communication and unentangled measurements. We propose a protocol that solves quantum inner product estimation with $k$-qubit one-way quantum communication and unentangled local measurements using $O(median\{1/\epsilon^2,2^{n/2}/\epsilon,2^{n-k}/\epsilon^2\})$ copies of $\rho$ and $\sigma$. Our protocol can be modified to estimate the purity of an unknown quantum state $\rho$ using $k$-qubit quantum memory with the same complexity. We prove that arbitrary protocols with $k$-qubit quantum memory that estimate purity to error $\epsilon$ require $\Omega(median\{1/\epsilon^2,2^{n/2}/\sqrt{\epsilon},2^{n-k}/\epsilon^2\})$ copies of $\rho$. This indicates the same lower bound for quantum inner product estimation with one-way $k$-qubit quantum communication and classical communication, and unentangled local measurements. For purity estimation, we further improve the lower bound to $\Omega(\max\{1/\epsilon^2,2^{n/2}/\epsilon\})$ for any protocols using an identical single-copy projection-valued measurement. Additionally, we investigate a decisional variant of quantum distributed inner product estimation without quantum communication for mixed state and provide a lower bound on the sample complexity.

On the average-case complexity of learning output distributions of quantum circuits

In this work, we show that learning the output distributions of brickwork random quantum circuits is average-case hard in the statistical query model. This learning model is widely used as an abstract computational model for most generic learning algorithms. In particular, for brickwork random quantum circuits on $n$ qubits of depth $d$, we show three main results: - At super logarithmic circuit depth $d=\omega(\log(n))$, any learning algorithm requires super polynomially many queries to achieve a constant probability of success over the randomly drawn instance. - There exists a $d=O(n)$, such that any learning algorithm requires $\Omega(2^n)$ queries to achieve a $O(2^{-n})$ probability of success over the randomly drawn instance. - At infinite circuit depth $d\to\infty$, any learning algorithm requires $2^{2^{\Omega(n)}}$ many queries to achieve a $2^{-2^{\Omega(n)}}$ probability of success over the randomly drawn instance. As an auxiliary result of independent interest, we show that the output distribution of a brickwork random quantum circuit is constantly far from any fixed distribution in total variation distance with probability $1-O(2^{-n})$, which confirms a variant of a conjecture by Aaronson and Chen.

A single $T$-gate makes distribution learning hard

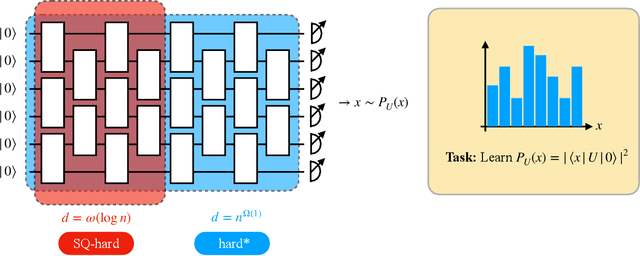
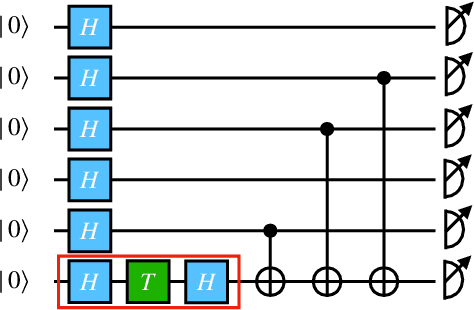
The task of learning a probability distribution from samples is ubiquitous across the natural sciences. The output distributions of local quantum circuits form a particularly interesting class of distributions, of key importance both to quantum advantage proposals and a variety of quantum machine learning algorithms. In this work, we provide an extensive characterization of the learnability of the output distributions of local quantum circuits. Our first result yields insight into the relationship between the efficient learnability and the efficient simulatability of these distributions. Specifically, we prove that the density modelling problem associated with Clifford circuits can be efficiently solved, while for depth $d=n^{\Omega(1)}$ circuits the injection of a single $T$-gate into the circuit renders this problem hard. This result shows that efficient simulatability does not imply efficient learnability. Our second set of results provides insight into the potential and limitations of quantum generative modelling algorithms. We first show that the generative modelling problem associated with depth $d=n^{\Omega(1)}$ local quantum circuits is hard for any learning algorithm, classical or quantum. As a consequence, one cannot use a quantum algorithm to gain a practical advantage for this task. We then show that, for a wide variety of the most practically relevant learning algorithms -- including hybrid-quantum classical algorithms -- even the generative modelling problem associated with depth $d=\omega(\log(n))$ Clifford circuits is hard. This result places limitations on the applicability of near-term hybrid quantum-classical generative modelling algorithms.

Learnability of the output distributions of local quantum circuits

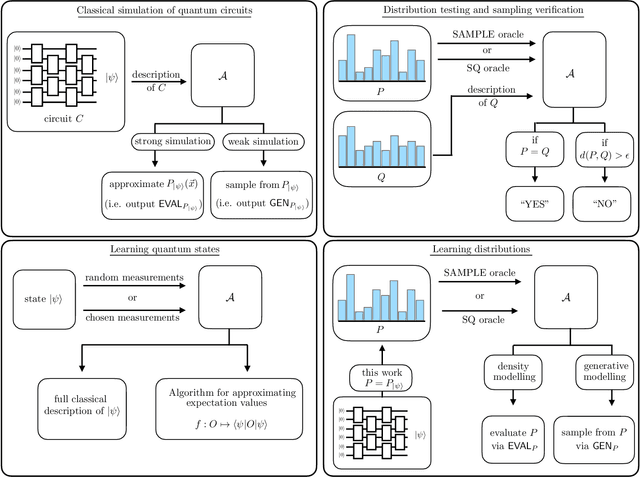
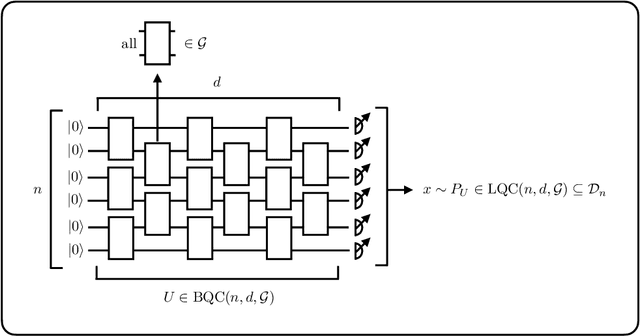
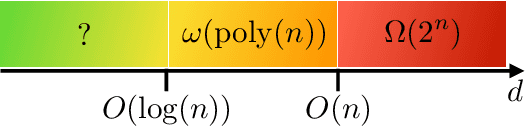
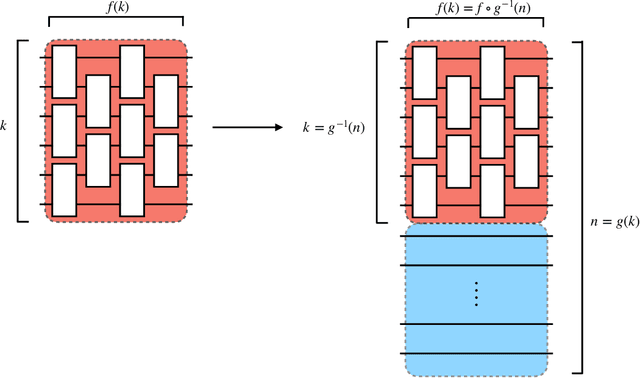
There is currently a large interest in understanding the potential advantages quantum devices can offer for probabilistic modelling. In this work we investigate, within two different oracle models, the probably approximately correct (PAC) learnability of quantum circuit Born machines, i.e., the output distributions of local quantum circuits. We first show a negative result, namely, that the output distributions of super-logarithmic depth Clifford circuits are not sample-efficiently learnable in the statistical query model, i.e., when given query access to empirical expectation values of bounded functions over the sample space. This immediately implies the hardness, for both quantum and classical algorithms, of learning from statistical queries the output distributions of local quantum circuits using any gate set which includes the Clifford group. As many practical generative modelling algorithms use statistical queries -- including those for training quantum circuit Born machines -- our result is broadly applicable and strongly limits the possibility of a meaningful quantum advantage for learning the output distributions of local quantum circuits. As a positive result, we show that in a more powerful oracle model, namely when directly given access to samples, the output distributions of local Clifford circuits are computationally efficiently PAC learnable by a classical learner. Our results are equally applicable to the problems of learning an algorithm for generating samples from the target distribution (generative modelling) and learning an algorithm for evaluating its probabilities (density modelling). They provide the first rigorous insights into the learnability of output distributions of local quantum circuits from the probabilistic modelling perspective.