On the sample complexity of purity and inner product estimation

We study the sample complexity of the prototypical tasks quantum purity estimation and quantum inner product estimation. In purity estimation, we are to estimate $tr(\rho^2)$ of an unknown quantum state $\rho$ to additive error $\epsilon$. Meanwhile, for quantum inner product estimation, Alice and Bob are to estimate $tr(\rho\sigma)$ to additive error $\epsilon$ given copies of unknown quantum state $\rho$ and $\sigma$ using classical communication and restricted quantum communication. In this paper, we show a strong connection between the sample complexity of purity estimation with bounded quantum memory and inner product estimation with bounded quantum communication and unentangled measurements. We propose a protocol that solves quantum inner product estimation with $k$-qubit one-way quantum communication and unentangled local measurements using $O(median\{1/\epsilon^2,2^{n/2}/\epsilon,2^{n-k}/\epsilon^2\})$ copies of $\rho$ and $\sigma$. Our protocol can be modified to estimate the purity of an unknown quantum state $\rho$ using $k$-qubit quantum memory with the same complexity. We prove that arbitrary protocols with $k$-qubit quantum memory that estimate purity to error $\epsilon$ require $\Omega(median\{1/\epsilon^2,2^{n/2}/\sqrt{\epsilon},2^{n-k}/\epsilon^2\})$ copies of $\rho$. This indicates the same lower bound for quantum inner product estimation with one-way $k$-qubit quantum communication and classical communication, and unentangled local measurements. For purity estimation, we further improve the lower bound to $\Omega(\max\{1/\epsilon^2,2^{n/2}/\epsilon\})$ for any protocols using an identical single-copy projection-valued measurement. Additionally, we investigate a decisional variant of quantum distributed inner product estimation without quantum communication for mixed state and provide a lower bound on the sample complexity.

Stabilizer bootstrapping: A recipe for efficient agnostic tomography and magic estimation

We study the task of agnostic tomography: given copies of an unknown $n$-qubit state $\rho$ which has fidelity $\tau$ with some state in a given class $C$, find a state which has fidelity $\ge \tau - \epsilon$ with $\rho$. We give a new framework, stabilizer bootstrapping, for designing computationally efficient protocols for this task, and use this to get new agnostic tomography protocols for the following classes: Stabilizer states: We give a protocol that runs in time $\mathrm{poly}(n,1/\epsilon)\cdot (1/\tau)^{O(\log(1/\tau))}$, answering an open question posed by Grewal, Iyer, Kretschmer, Liang [40] and Anshu and Arunachalam [6]. Previous protocols ran in time $\mathrm{exp}(\Theta(n))$ or required $\tau>\cos^2(\pi/8)$. States with stabilizer dimension $n - t$: We give a protocol that runs in time $n^3\cdot(2^t/\tau)^{O(\log(1/\epsilon))}$, extending recent work on learning quantum states prepared by circuits with few non-Clifford gates, which only applied in the realizable setting where $\tau = 1$ [30, 37, 46, 61]. Discrete product states: If $C = K^{\otimes n}$ for some $\mu$-separated discrete set $K$ of single-qubit states, we give a protocol that runs in time $(n/\mu)^{O((1 + \log (1/\tau))/\mu)}/\epsilon^2$. This strictly generalizes a prior guarantee which applied to stabilizer product states [39]. For stabilizer product states, we give a further improved protocol that runs in time $(n^2/\epsilon^2)\cdot (1/\tau)^{O(\log(1/\tau))}$. As a corollary, we give the first protocol for estimating stabilizer fidelity, a standard measure of magic for quantum states, to error $\epsilon$ in $n^3 \mathrm{quasipoly}(1/\epsilon)$ time.

Quantum-Classical Separations in Shallow-Circuit-Based Learning with and without Noises

We study quantum-classical separations between classical and quantum supervised learning models based on constant depth (i.e., shallow) circuits, in scenarios with and without noises. We construct a classification problem defined by a noiseless shallow quantum circuit and rigorously prove that any classical neural network with bounded connectivity requires logarithmic depth to output correctly with a larger-than-exponentially-small probability. This unconditional near-optimal quantum-classical separation originates from the quantum nonlocality property that distinguishes quantum circuits from their classical counterparts. We further derive the noise thresholds for demonstrating such a separation on near-term quantum devices under the depolarization noise model. We prove that this separation will persist if the noise strength is upper bounded by an inverse polynomial with respect to the system size, and vanish if the noise strength is greater than an inverse polylogarithmic function. In addition, for quantum devices with constant noise strength, we prove that no super-polynomial classical-quantum separation exists for any classification task defined by shallow Clifford circuits, independent of the structures of the circuits that specify the learning models.

Futility and utility of a few ancillas for Pauli channel learning

In this paper we revisit one of the prototypical tasks for characterizing the structure of noise in quantum devices, estimating the eigenvalues of an $n$-qubit Pauli noise channel. Prior work (Chen et al., 2022) established exponential lower bounds for this task for algorithms with limited quantum memory. We first improve upon their lower bounds and show: (1) Any algorithm without quantum memory must make $\Omega(2^n/\epsilon^2)$ measurements to estimate each eigenvalue within error $\epsilon$. This is tight and implies the randomized benchmarking protocol is optimal, resolving an open question of (Flammia and Wallman, 2020). (2) Any algorithm with $\le k$ ancilla qubits of quantum memory must make $\Omega(2^{(n-k)/3})$ queries to the unknown channel. Crucially, unlike in (Chen et al., 2022), our bound holds even if arbitrary adaptive control and channel concatenation are allowed. In fact these lower bounds, like those of (Chen et al., 2022), hold even for the easier hypothesis testing problem of determining whether the underlying channel is completely depolarizing or has exactly one other nontrivial eigenvalue. Surprisingly, we show that: (3) With only $k=2$ ancilla qubits of quantum memory, there is an algorithm that solves this hypothesis testing task with high probability using a single measurement. Note that (3) does not contradict (2) as the protocol concatenates exponentially many queries to the channel before the measurement. This result suggests a novel mechanism by which channel concatenation and $O(1)$ qubits of quantum memory could work in tandem to yield striking speedups for quantum process learning that are not possible for quantum state learning.

Enhancing Quantum Adversarial Robustness by Randomized Encodings

The interplay between quantum physics and machine learning gives rise to the emergent frontier of quantum machine learning, where advanced quantum learning models may outperform their classical counterparts in solving certain challenging problems. However, quantum learning systems are vulnerable to adversarial attacks: adding tiny carefully-crafted perturbations on legitimate input samples can cause misclassifications. To address this issue, we propose a general scheme to protect quantum learning systems from adversarial attacks by randomly encoding the legitimate data samples through unitary or quantum error correction encoders. In particular, we rigorously prove that both global and local random unitary encoders lead to exponentially vanishing gradients (i.e. barren plateaus) for any variational quantum circuits that aim to add adversarial perturbations, independent of the input data and the inner structures of adversarial circuits and quantum classifiers. In addition, we prove a rigorous bound on the vulnerability of quantum classifiers under local unitary adversarial attacks. We show that random black-box quantum error correction encoders can protect quantum classifiers against local adversarial noises and their robustness increases as we concatenate error correction codes. To quantify the robustness enhancement, we adapt quantum differential privacy as a measure of the prediction stability for quantum classifiers. Our results establish versatile defense strategies for quantum classifiers against adversarial perturbations, which provide valuable guidance to enhance the reliability and security for both near-term and future quantum learning technologies.

Weighted Quantum Channel Compiling through Proximal Policy Optimization

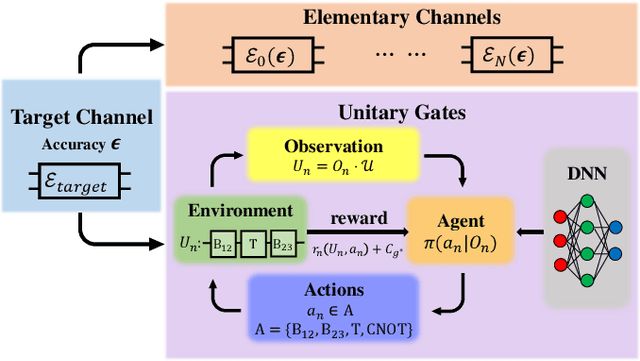
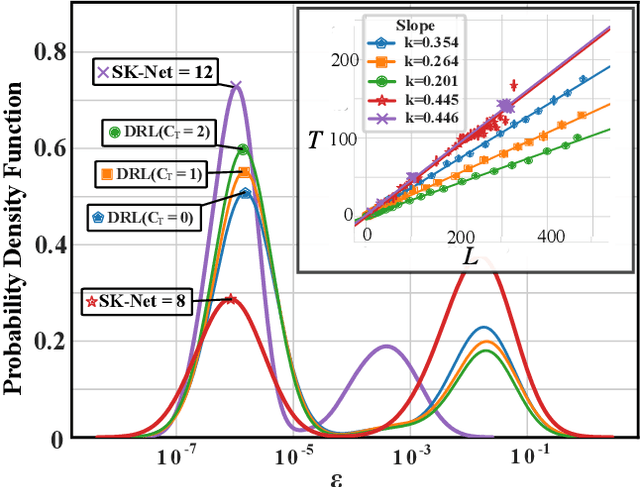
We propose a general and systematic strategy to compile arbitrary quantum channels without using ancillary qubits, based on proximal policy optimization -- a powerful deep reinforcement learning algorithm. We rigorously prove that, in sharp contrast to the case of compiling unitary gates, it is impossible to compile an arbitrary channel to arbitrary precision with any given finite elementary channel set, regardless of the length of the decomposition sequence. However, for a fixed accuracy $\epsilon$ one can construct a universal set with constant number of $\epsilon$-dependent elementary channels, such that an arbitrary quantum channel can be decomposed into a sequence of these elementary channels followed by a unitary gate, with the sequence length bounded by $O(\frac{1}{\epsilon}\log\frac{1}{\epsilon})$. Through a concrete example concerning topological compiling of Majorana fermions, we show that our proposed algorithm can conveniently and effectively reduce the use of expensive elementary gates through adding the weighted cost into the reward function of the proximal policy optimization.

Universal Adversarial Examples and Perturbations for Quantum Classifiers

Quantum machine learning explores the interplay between machine learning and quantum physics, which may lead to unprecedented perspectives for both fields. In fact, recent works have shown strong evidences that quantum computers could outperform classical computers in solving certain notable machine learning tasks. Yet, quantum learning systems may also suffer from the vulnerability problem: adding a tiny carefully-crafted perturbation to the legitimate input data would cause the systems to make incorrect predictions at a notably high confidence level. In this paper, we study the universality of adversarial examples and perturbations for quantum classifiers. Through concrete examples involving classifications of real-life images and quantum phases of matter, we show that there exist universal adversarial examples that can fool a set of different quantum classifiers. We prove that for a set of $k$ classifiers with each receiving input data of $n$ qubits, an $O(\frac{\ln k} {2^n})$ increase of the perturbation strength is enough to ensure a moderate universal adversarial risk. In addition, for a given quantum classifier we show that there exist universal adversarial perturbations, which can be added to different legitimate samples and make them to be adversarial examples for the classifier. Our results reveal the universality perspective of adversarial attacks for quantum machine learning systems, which would be crucial for practical applications of both near-term and future quantum technologies in solving machine learning problems.