Video-MSR: Benchmarking Multi-hop Spatial Reasoning Capabilities of MLLMs

Spatial reasoning has emerged as a critical capability for Multimodal Large Language Models (MLLMs), drawing increasing attention and rapid advancement. However, existing benchmarks primarily focus on single-step perception-to-judgment tasks, leaving scenarios requiring complex visual-spatial logical chains significantly underexplored. To bridge this gap, we introduce Video-MSR, the first benchmark specifically designed to evaluate Multi-hop Spatial Reasoning (MSR) in dynamic video scenarios. Video-MSR systematically probes MSR capabilities through four distinct tasks: Constrained Localization, Chain-based Reference Retrieval, Route Planning, and Counterfactual Physical Deduction. Our benchmark comprises 3,052 high-quality video instances with 4,993 question-answer pairs, constructed via a scalable, visually-grounded pipeline combining advanced model generation with rigorous human verification. Through a comprehensive evaluation of 20 state-of-the-art MLLMs, we uncover significant limitations, revealing that while models demonstrate proficiency in surface-level perception, they exhibit distinct performance drops in MSR tasks, frequently suffering from spatial disorientation and hallucination during multi-step deductions. To mitigate these shortcomings and empower models with stronger MSR capabilities, we further curate MSR-9K, a specialized instruction-tuning dataset, and fine-tune Qwen-VL, achieving a +7.82% absolute improvement on Video-MSR. Our results underscore the efficacy of multi-hop spatial instruction data and establish Video-MSR as a vital foundation for future research. The code and data will be available at https://github.com/ruiz-nju/Video-MSR.

Decide Then Retrieve: A Training-Free Framework with Uncertainty-Guided Triggering and Dual-Path Retrieval

Retrieval-augmented generation (RAG) enhances large language models (LLMs) by incorporating external knowledge, but existing approaches indiscriminately trigger retrieval and rely on single-path evidence construction, often introducing noise and limiting performance gains. In this work, we propose Decide Then Retrieve (DTR), a training-free framework that adaptively determines when retrieval is necessary and how external information should be selected. DTR leverages generation uncertainty to guide retrieval triggering and introduces a dual-path retrieval mechanism with adaptive information selection to better handle sparse and ambiguous queries. Extensive experiments across five open-domain QA benchmarks, multiple model scales, and different retrievers demonstrate that DTR consistently improves EM and F1 over standard RAG and strong retrieval-enhanced baselines, while reducing unnecessary retrievals. The code and data used in this paper are available at https://github.com/ChenWangHKU/DTR.

BBox DocVQA: A Large Scale Bounding Box Grounded Dataset for Enhancing Reasoning in Document Visual Question Answer

Document Visual Question Answering (DocVQA) is a fundamental task for multimodal document understanding and a key testbed for vision language reasoning. However, most existing DocVQA datasets are limited to the page level and lack fine grained spatial grounding, constraining the interpretability and reasoning capability of Vision Language Models (VLMs). To address this gap, we introduce BBox DocVQA a large scale, bounding box grounded dataset designed to enhance spatial reasoning and evidence localization in visual documents. We further present an automated construction pipeline, Segment Judge and Generate, which integrates a segment model for region segmentation, a VLM for semantic judgment, and another advanced VLM for question answer generation, followed by human verification for quality assurance. The resulting dataset contains 3.6 K diverse documents and 32 K QA pairs, encompassing single and multi region as well as single and multi page scenarios. Each QA instance is grounded on explicit bounding boxes, enabling fine grained evaluation of spatial semantic alignment. Benchmarking multiple state of the art VLMs (e.g., GPT 5, Qwen2.5 VL, and InternVL) on BBox DocVQA reveals persistent challenges in spatial grounding and reasoning accuracy. Furthermore, fine tuning on BBox DocVQA substantially improves both bounding box localization and answer generation, validating its effectiveness for enhancing the reasoning ability of VLMs. Our dataset and code will be publicly released to advance research on interpretable and spatially grounded vision language reasoning.

Reducing Cognitive Load in Multi-Agent Reinforcement Learning for Mathematical Problem Solving: Decoupling Reasoning and Code Generation

Current tool-integrated mathematical reasoning systems often adopt a single-agent paradigm, where one large language model handles problem reasoning, code generation, and code execution in an integrated workflow. While this design eases coordination, we hypothesize that it imposes cognitive load interference, as the agent must interleave long-horizon reasoning with precise program synthesis. We validate this hypothesis through a controlled comparison between a reasoning-only agent and a reasoning-plus-code agent, finding that the latter produces significantly fewer correct reasoning paths despite having tool-calling capabilities. To address this, we propose a dual-agent hybrid framework: a Reasoning Agent performs stepwise problem decomposition, and a Code Agent handles code generation and execution. Training combines imitation learning and reinforcement learning: the Code Agent receives strong rewards for matching intermediate ground-truth programs and weaker rewards for valid execution, while the Reasoning Agent is optimized chiefly via final-answer accuracy using advantage estimation to credit intermediate steps. This decoupled role design reduces cognitive interference and promotes stable reasoning-coding coordination.

Cross-LoRA: A Data-Free LoRA Transfer Framework across Heterogeneous LLMs

Traditional parameter-efficient fine-tuning (PEFT) methods such as LoRA are tightly coupled with the base model architecture, which constrains their applicability across heterogeneous pretrained large language models (LLMs). To address this limitation, we introduce Cross-LoRA, a data-free framework for transferring LoRA modules between diverse base models without requiring additional training data. Cross-LoRA consists of two key components: (a) LoRA-Align, which performs subspace alignment between source and target base models through rank-truncated singular value decomposition (SVD) and Frobenius-optimal linear transformation, ensuring compatibility under dimension mismatch; and (b) LoRA-Shift, which applies the aligned subspaces to project source LoRA weight updates into the target model parameter space. Both components are data-free, training-free, and enable lightweight adaptation on a commodity GPU in 20 minutes. Experiments on ARCs, OBOA and HellaSwag show that Cross-LoRA achieves relative gains of up to 5.26% over base models. Across other commonsense reasoning benchmarks, Cross-LoRA maintains performance comparable to that of directly trained LoRA adapters.

PAIRS: Parametric-Verified Adaptive Information Retrieval and Selection for Efficient RAG

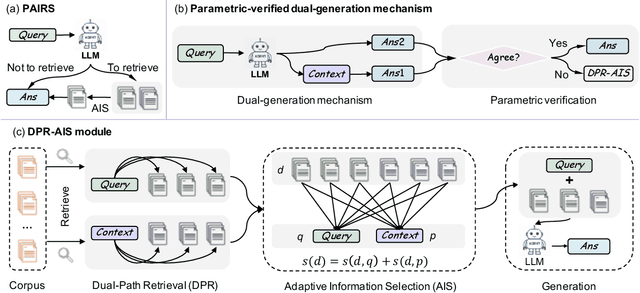
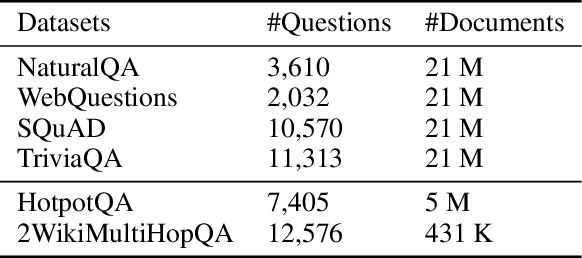
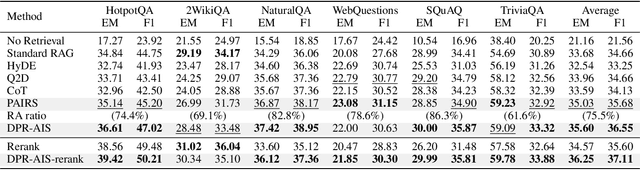
Retrieval-Augmented Generation (RAG) has become a cornerstone technique for enhancing large language models (LLMs) with external knowledge. However, current RAG systems face two critical limitations: (1) they inefficiently retrieve information for every query, including simple questions that could be resolved using the LLM's parametric knowledge alone, and (2) they risk retrieving irrelevant documents when queries contain sparse information signals. To address these gaps, we introduce Parametric-verified Adaptive Information Retrieval and Selection (PAIRS), a training-free framework that integrates parametric and retrieved knowledge to adaptively determine whether to retrieve and how to select external information. Specifically, PAIRS employs a dual-path generation mechanism: First, the LLM produces both a direct answer and a context-augmented answer using self-generated pseudo-context. When these outputs converge, PAIRS bypasses external retrieval entirely, dramatically improving the RAG system's efficiency. For divergent cases, PAIRS activates a dual-path retrieval (DPR) process guided by both the original query and self-generated contextual signals, followed by an Adaptive Information Selection (AIS) module that filters documents through weighted similarity to both sources. This simple yet effective approach can not only enhance efficiency by eliminating unnecessary retrievals but also improve accuracy through contextually guided retrieval and adaptive information selection. Experimental results on six question-answering (QA) benchmarks show that PAIRS reduces retrieval costs by around 25% (triggering for only 75% of queries) while still improving accuracy-achieving +1.1% EM and +1.0% F1 over prior baselines on average.

Solving excited states for long-range interacting trapped ions with neural networks

The computation of excited states in strongly interacting quantum many-body systems is of fundamental importance. Yet, it is notoriously challenging due to the exponential scaling of the Hilbert space dimension with the system size. Here, we introduce a neural network-based algorithm that can simultaneously output multiple low-lying excited states of a quantum many-body spin system in an accurate and efficient fashion. This algorithm, dubbed the neural quantum excited-state (NQES) algorithm, requires no explicit orthogonalization of the states and is generally applicable to higher dimensions. We demonstrate, through concrete examples including the Haldane-Shastry model with all-to-all interactions, that the NQES algorithm is capable of efficiently computing multiple excited states and their related observable expectations. In addition, we apply the NQES algorithm to two classes of long-range interacting trapped-ion systems in a two-dimensional Wigner crystal. For non-decaying all-to-all interactions with alternating signs, our computed low-lying excited states bear spatial correlation patterns similar to those of the ground states, which closely match recent experimental observations that the quasi-adiabatically prepared state accurately reproduces analytical ground-state correlations. For a system of up to 300 ions with power-law decaying antiferromagnetic interactions, we successfully uncover its gap scaling and correlation features. Our results establish a scalable and efficient algorithm for computing excited states of interacting quantum many-body systems, which holds potential applications ranging from benchmarking quantum devices to photoisomerization.

Quantum automated learning with provable and explainable trainability

Machine learning is widely believed to be one of the most promising practical applications of quantum computing. Existing quantum machine learning schemes typically employ a quantum-classical hybrid approach that relies crucially on gradients of model parameters. Such an approach lacks provable convergence to global minima and will become infeasible as quantum learning models scale up. Here, we introduce quantum automated learning, where no variational parameter is involved and the training process is converted to quantum state preparation. In particular, we encode training data into unitary operations and iteratively evolve a random initial state under these unitaries and their inverses, with a target-oriented perturbation towards higher prediction accuracy sandwiched in between. Under reasonable assumptions, we rigorously prove that the evolution converges exponentially to the desired state corresponding to the global minimum of the loss function. We show that such a training process can be understood from the perspective of preparing quantum states by imaginary time evolution, where the data-encoded unitaries together with target-oriented perturbations would train the quantum learning model in an automated fashion. We further prove that the quantum automated learning paradigm features good generalization ability with the generalization error upper bounded by the ratio between a logarithmic function of the Hilbert space dimension and the number of training samples. In addition, we carry out extensive numerical simulations on real-life images and quantum data to demonstrate the effectiveness of our approach and validate the assumptions. Our results establish an unconventional quantum learning strategy that is gradient-free with provable and explainable trainability, which would be crucial for large-scale practical applications of quantum computing in machine learning scenarios.

Quantum delegated and federated learning via quantum homomorphic encryption

Quantum learning models hold the potential to bring computational advantages over the classical realm. As powerful quantum servers become available on the cloud, ensuring the protection of clients' private data becomes crucial. By incorporating quantum homomorphic encryption schemes, we present a general framework that enables quantum delegated and federated learning with a computation-theoretical data privacy guarantee. We show that learning and inference under this framework feature substantially lower communication complexity compared with schemes based on blind quantum computing. In addition, in the proposed quantum federated learning scenario, there is less computational burden on local quantum devices from the client side, since the server can operate on encrypted quantum data without extracting any information. We further prove that certain quantum speedups in supervised learning carry over to private delegated learning scenarios employing quantum kernel methods. Our results provide a valuable guide toward privacy-guaranteed quantum learning on the cloud, which may benefit future studies and security-related applications.

Quantum-machine-assisted Drug Discovery: Survey and Perspective

Drug discovery and development is a highly complex and costly endeavor, typically requiring over a decade and substantial financial investment to bring a new drug to market. Traditional computer-aided drug design (CADD) has made significant progress in accelerating this process, but the development of quantum computing offers potential due to its unique capabilities. This paper discusses the integration of quantum computing into drug discovery and development, focusing on how quantum technologies might accelerate and enhance various stages of the drug development cycle. Specifically, we explore the application of quantum computing in addressing challenges related to drug discovery, such as molecular simulation and the prediction of drug-target interactions, as well as the optimization of clinical trial outcomes. By leveraging the inherent capabilities of quantum computing, we might be able to reduce the time and cost associated with bringing new drugs to market, ultimately benefiting public health.