Probing many-body Bell correlation depth with superconducting qubits

Quantum nonlocality describes a stronger form of quantum correlation than that of entanglement. It refutes Einstein's belief of local realism and is among the most distinctive and enigmatic features of quantum mechanics. It is a crucial resource for achieving quantum advantages in a variety of practical applications, ranging from cryptography and certified random number generation via self-testing to machine learning. Nevertheless, the detection of nonlocality, especially in quantum many-body systems, is notoriously challenging. Here, we report an experimental certification of genuine multipartite Bell correlations, which signal nonlocality in quantum many-body systems, up to 24 qubits with a fully programmable superconducting quantum processor. In particular, we employ energy as a Bell correlation witness and variationally decrease the energy of a many-body system across a hierarchy of thresholds, below which an increasing Bell correlation depth can be certified from experimental data. As an illustrating example, we variationally prepare the low-energy state of a two-dimensional honeycomb model with 73 qubits and certify its Bell correlations by measuring an energy that surpasses the corresponding classical bound with up to 48 standard deviations. In addition, we variationally prepare a sequence of low-energy states and certify their genuine multipartite Bell correlations up to 24 qubits via energies measured efficiently by parity oscillation and multiple quantum coherence techniques. Our results establish a viable approach for preparing and certifying multipartite Bell correlations, which provide not only a finer benchmark beyond entanglement for quantum devices, but also a valuable guide towards exploiting multipartite Bell correlation in a wide spectrum of practical applications.

Expressibility-induced Concentration of Quantum Neural Tangent Kernels

Quantum tangent kernel methods provide an efficient approach to analyzing the performance of quantum machine learning models in the infinite-width limit, which is of crucial importance in designing appropriate circuit architectures for certain learning tasks. Recently, they have been adapted to describe the convergence rate of training errors in quantum neural networks in an analytical manner. Here, we study the connections between the trainability and expressibility of quantum tangent kernel models. In particular, for global loss functions, we rigorously prove that high expressibility of both the global and local quantum encodings can lead to exponential concentration of quantum tangent kernel values to zero. Whereas for local loss functions, such issue of exponential concentration persists owing to the high expressibility, but can be partially mitigated. We further carry out extensive numerical simulations to support our analytical theories. Our discoveries unveil a pivotal characteristic of quantum neural tangent kernels, offering valuable insights for the design of wide quantum variational circuit models in practical applications.

Quantum Neural Network Classifiers: A Tutorial

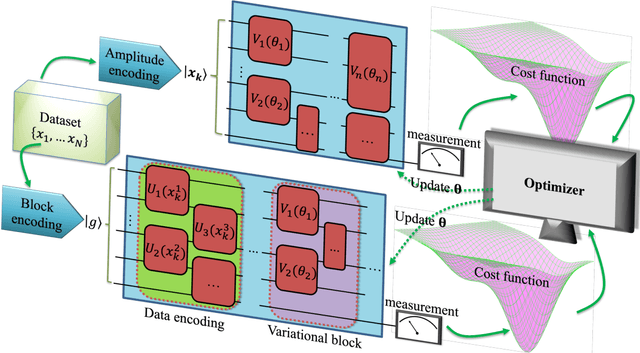
Machine learning has achieved dramatic success over the past decade, with applications ranging from face recognition to natural language processing. Meanwhile, rapid progress has been made in the field of quantum computation including developing both powerful quantum algorithms and advanced quantum devices. The interplay between machine learning and quantum physics holds the intriguing potential for bringing practical applications to the modern society. Here, we focus on quantum neural networks in the form of parameterized quantum circuits. We will mainly discuss different structures and encoding strategies of quantum neural networks for supervised learning tasks, and benchmark their performance utilizing Yao.jl, a quantum simulation package written in Julia Language. The codes are efficient, aiming to provide convenience for beginners in scientific works such as developing powerful variational quantum learning models and assisting the corresponding experimental demonstrations.

Quantum Continual Learning Overcoming Catastrophic Forgetting

Catastrophic forgetting describes the fact that machine learning models will likely forget the knowledge of previously learned tasks after the learning process of a new one. It is a vital problem in the continual learning scenario and recently has attracted tremendous concern across different communities. In this paper, we explore the catastrophic forgetting phenomena in the context of quantum machine learning. We find that, similar to those classical learning models based on neural networks, quantum learning systems likewise suffer from such forgetting problem in classification tasks emerging from various application scenes. We show that based on the local geometrical information in the loss function landscape of the trained model, a uniform strategy can be adapted to overcome the forgetting problem in the incremental learning setting. Our results uncover the catastrophic forgetting phenomena in quantum machine learning and offer a practical method to overcome this problem, which opens a new avenue for exploring potential quantum advantages towards continual learning.