MinosEval: Distinguishing Factoid and Non-Factoid for Tailored Open-Ended QA Evaluation with LLMs

Open-ended question answering (QA) is a key task for evaluating the capabilities of large language models (LLMs). Compared to closed-ended QA, it demands longer answer statements, more nuanced reasoning processes, and diverse expressions, making refined and interpretable automatic evaluation both crucial and challenging. Traditional metrics like ROUGE and BERTScore struggle to capture semantic similarities due to different patterns between model responses and reference answers. Current LLM-based evaluation approaches, such as pairwise or listwise comparisons of candidate answers, lack intuitive interpretability. While pointwise scoring of each response provides some descriptions, it fails to adapt across different question contents. Most notably, existing methods overlook the distinction between factoid and non-factoid questions. To address these challenges, we propose \textbf{MinosEval}, a novel evaluation method that first distinguishes open-ended questions and then ranks candidate answers using different evaluation strategies. For factoid questions, it applies an adaptive key-point scoring strategy, while for non-factoid questions, it uses an instance-aware listwise ranking strategy. Experiments on multiple open-ended QA datasets, including self-built ones with more candidate responses to complement community resources, show that MinosEval better aligns with human annotations and offers more interpretable results.

OpenHOI: Open-World Hand-Object Interaction Synthesis with Multimodal Large Language Model

Understanding and synthesizing realistic 3D hand-object interactions (HOI) is critical for applications ranging from immersive AR/VR to dexterous robotics. Existing methods struggle with generalization, performing well on closed-set objects and predefined tasks but failing to handle unseen objects or open-vocabulary instructions. We introduce OpenHOI, the first framework for open-world HOI synthesis, capable of generating long-horizon manipulation sequences for novel objects guided by free-form language commands. Our approach integrates a 3D Multimodal Large Language Model (MLLM) fine-tuned for joint affordance grounding and semantic task decomposition, enabling precise localization of interaction regions (e.g., handles, buttons) and breakdown of complex instructions (e.g., "Find a water bottle and take a sip") into executable sub-tasks. To synthesize physically plausible interactions, we propose an affordance-driven diffusion model paired with a training-free physics refinement stage that minimizes penetration and optimizes affordance alignment. Evaluations across diverse scenarios demonstrate OpenHOI's superiority over state-of-the-art methods in generalizing to novel object categories, multi-stage tasks, and complex language instructions. Our project page at \href{https://openhoi.github.io}

Neuro-Symbolic Query Compiler

Precise recognition of search intent in Retrieval-Augmented Generation (RAG) systems remains a challenging goal, especially under resource constraints and for complex queries with nested structures and dependencies. This paper presents QCompiler, a neuro-symbolic framework inspired by linguistic grammar rules and compiler design, to bridge this gap. It theoretically designs a minimal yet sufficient Backus-Naur Form (BNF) grammar $G[q]$ to formalize complex queries. Unlike previous methods, this grammar maintains completeness while minimizing redundancy. Based on this, QCompiler includes a Query Expression Translator, a Lexical Syntax Parser, and a Recursive Descent Processor to compile queries into Abstract Syntax Trees (ASTs) for execution. The atomicity of the sub-queries in the leaf nodes ensures more precise document retrieval and response generation, significantly improving the RAG system's ability to address complex queries.

Hierarchical Document Refinement for Long-context Retrieval-augmented Generation

Real-world RAG applications often encounter long-context input scenarios, where redundant information and noise results in higher inference costs and reduced performance. To address these challenges, we propose LongRefiner, an efficient plug-and-play refiner that leverages the inherent structural characteristics of long documents. LongRefiner employs dual-level query analysis, hierarchical document structuring, and adaptive refinement through multi-task learning on a single foundation model. Experiments on seven QA datasets demonstrate that LongRefiner achieves competitive performance in various scenarios while using 10x fewer computational costs and latency compared to the best baseline. Further analysis validates that LongRefiner is scalable, efficient, and effective, providing practical insights for real-world long-text RAG applications. Our code is available at https://github.com/ignorejjj/LongRefiner.

Ansatz-free Hamiltonian learning with Heisenberg-limited scaling

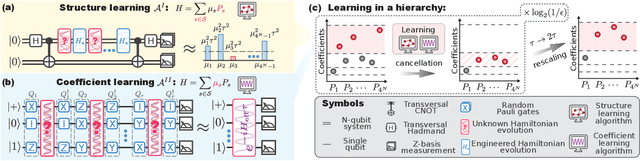
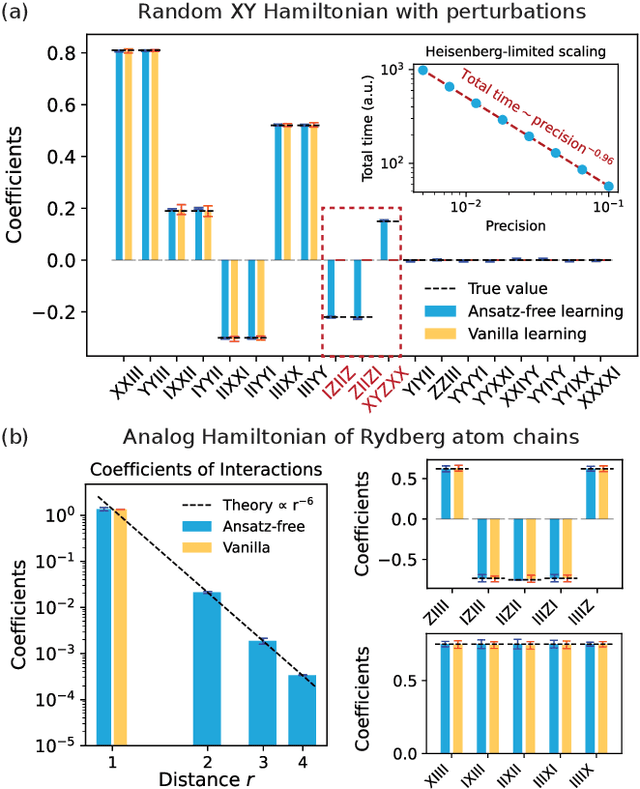
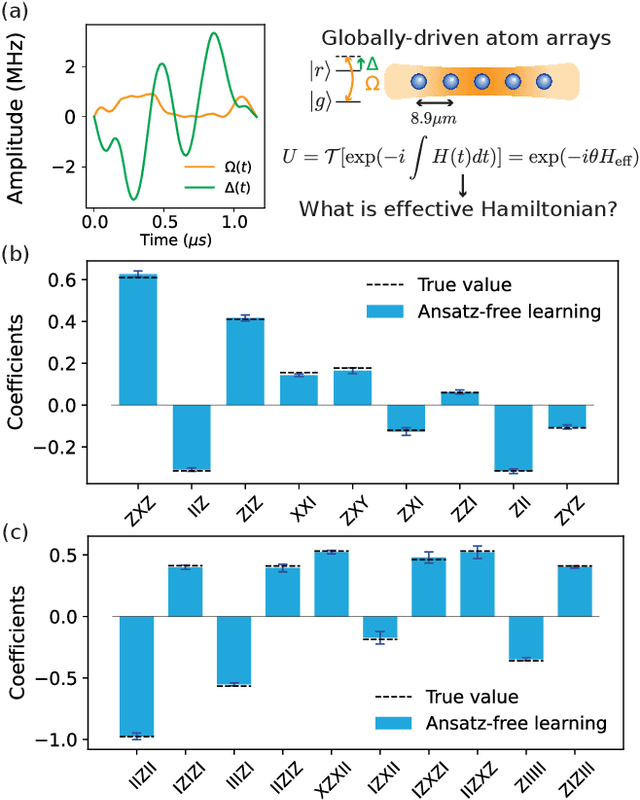
Learning the unknown interactions that govern a quantum system is crucial for quantum information processing, device benchmarking, and quantum sensing. The problem, known as Hamiltonian learning, is well understood under the assumption that interactions are local, but this assumption may not hold for arbitrary Hamiltonians. Previous methods all require high-order inverse polynomial dependency with precision, unable to surpass the standard quantum limit and reach the gold standard Heisenberg-limited scaling. Whether Heisenberg-limited Hamiltonian learning is possible without prior assumptions about the interaction structures, a challenge we term \emph{ansatz-free Hamiltonian learning}, remains an open question. In this work, we present a quantum algorithm to learn arbitrary sparse Hamiltonians without any structure constraints using only black-box queries of the system's real-time evolution and minimal digital controls to attain Heisenberg-limited scaling in estimation error. Our method is also resilient to state-preparation-and-measurement errors, enhancing its practical feasibility. Moreover, we establish a fundamental trade-off between total evolution time and quantum control on learning arbitrary interactions, revealing the intrinsic interplay between controllability and total evolution time complexity for any learning algorithm. These results pave the way for further exploration into Heisenberg-limited Hamiltonian learning in complex quantum systems under minimal assumptions, potentially enabling new benchmarking and verification protocols.

CMQCIC-Bench: A Chinese Benchmark for Evaluating Large Language Models in Medical Quality Control Indicator Calculation

Medical quality control indicators are essential to assess the qualifications of healthcare institutions for medical services. With the impressive performance of large language models (LLMs) like GPT-4 in the medical field, leveraging these technologies for the Medical Quality Control Indicator Calculation (MQCIC) presents a promising approach. In this work, (1) we introduce a real-world task MQCIC and propose an open-source Chinese electronic medical records (EMRs)-based dataset (CMQCIC-Bench) comprising 785 instances and 76 indicators. (2) We propose a semi-automatic method to enhance the rule representation. Then we propose the Clinical Facts-based Inferential Rule (CF-IR) method that disentangles the clinical fact verification and inferential rule reasoning actions. (3) We conduct comprehensive experiments on 20 representative LLMs, covering general and medical models. Our findings reveal that CF-IR outperforms Chain-of-Thought methods in MQCIC tasks. (4) We conduct an error analysis and investigate the capabilities of clinical fact verification and inferential rule reasoning, providing insights to improve performance in the MQCIC further. The dataset and code is available in this repo https://anonymous.4open.science/r/C-MQCIC-1151.

Quantum automated learning with provable and explainable trainability

Machine learning is widely believed to be one of the most promising practical applications of quantum computing. Existing quantum machine learning schemes typically employ a quantum-classical hybrid approach that relies crucially on gradients of model parameters. Such an approach lacks provable convergence to global minima and will become infeasible as quantum learning models scale up. Here, we introduce quantum automated learning, where no variational parameter is involved and the training process is converted to quantum state preparation. In particular, we encode training data into unitary operations and iteratively evolve a random initial state under these unitaries and their inverses, with a target-oriented perturbation towards higher prediction accuracy sandwiched in between. Under reasonable assumptions, we rigorously prove that the evolution converges exponentially to the desired state corresponding to the global minimum of the loss function. We show that such a training process can be understood from the perspective of preparing quantum states by imaginary time evolution, where the data-encoded unitaries together with target-oriented perturbations would train the quantum learning model in an automated fashion. We further prove that the quantum automated learning paradigm features good generalization ability with the generalization error upper bounded by the ratio between a logarithmic function of the Hilbert space dimension and the number of training samples. In addition, we carry out extensive numerical simulations on real-life images and quantum data to demonstrate the effectiveness of our approach and validate the assumptions. Our results establish an unconventional quantum learning strategy that is gradient-free with provable and explainable trainability, which would be crucial for large-scale practical applications of quantum computing in machine learning scenarios.

VTAO-BiManip: Masked Visual-Tactile-Action Pre-training with Object Understanding for Bimanual Dexterous Manipulation

Bimanual dexterous manipulation remains significant challenges in robotics due to the high DoFs of each hand and their coordination. Existing single-hand manipulation techniques often leverage human demonstrations to guide RL methods but fail to generalize to complex bimanual tasks involving multiple sub-skills. In this paper, we introduce VTAO-BiManip, a novel framework that combines visual-tactile-action pretraining with object understanding to facilitate curriculum RL to enable human-like bimanual manipulation. We improve prior learning by incorporating hand motion data, providing more effective guidance for dual-hand coordination than binary tactile feedback. Our pretraining model predicts future actions as well as object pose and size using masked multimodal inputs, facilitating cross-modal regularization. To address the multi-skill learning challenge, we introduce a two-stage curriculum RL approach to stabilize training. We evaluate our method on a bottle-cap unscrewing task, demonstrating its effectiveness in both simulated and real-world environments. Our approach achieves a success rate that surpasses existing visual-tactile pretraining methods by over 20%.

RetroLLM: Empowering Large Language Models to Retrieve Fine-grained Evidence within Generation

Large language models (LLMs) exhibit remarkable generative capabilities but often suffer from hallucinations. Retrieval-augmented generation (RAG) offers an effective solution by incorporating external knowledge, but existing methods still face several limitations: additional deployment costs of separate retrievers, redundant input tokens from retrieved text chunks, and the lack of joint optimization of retrieval and generation. To address these issues, we propose \textbf{RetroLLM}, a unified framework that integrates retrieval and generation into a single, cohesive process, enabling LLMs to directly generate fine-grained evidence from the corpus with constrained decoding. Moreover, to mitigate false pruning in the process of constrained evidence generation, we introduce (1) hierarchical FM-Index constraints, which generate corpus-constrained clues to identify a subset of relevant documents before evidence generation, reducing irrelevant decoding space; and (2) a forward-looking constrained decoding strategy, which considers the relevance of future sequences to improve evidence accuracy. Extensive experiments on five open-domain QA datasets demonstrate RetroLLM's superior performance across both in-domain and out-of-domain tasks. The code is available at \url{https://github.com/sunnynexus/RetroLLM}.

No-Free-Lunch Theories for Tensor-Network Machine Learning Models

Tensor network machine learning models have shown remarkable versatility in tackling complex data-driven tasks, ranging from quantum many-body problems to classical pattern recognitions. Despite their promising performance, a comprehensive understanding of the underlying assumptions and limitations of these models is still lacking. In this work, we focus on the rigorous formulation of their no-free-lunch theorem -- essential yet notoriously challenging to formalize for specific tensor network machine learning models. In particular, we rigorously analyze the generalization risks of learning target output functions from input data encoded in tensor network states. We first prove a no-free-lunch theorem for machine learning models based on matrix product states, i.e., the one-dimensional tensor network states. Furthermore, we circumvent the challenging issue of calculating the partition function for two-dimensional Ising model, and prove the no-free-lunch theorem for the case of two-dimensional projected entangled-pair state, by introducing the combinatorial method associated to the "puzzle of polyominoes". Our findings reveal the intrinsic limitations of tensor network-based learning models in a rigorous fashion, and open up an avenue for future analytical exploration of both the strengths and limitations of quantum-inspired machine learning frameworks.