Quantum automated learning with provable and explainable trainability

Machine learning is widely believed to be one of the most promising practical applications of quantum computing. Existing quantum machine learning schemes typically employ a quantum-classical hybrid approach that relies crucially on gradients of model parameters. Such an approach lacks provable convergence to global minima and will become infeasible as quantum learning models scale up. Here, we introduce quantum automated learning, where no variational parameter is involved and the training process is converted to quantum state preparation. In particular, we encode training data into unitary operations and iteratively evolve a random initial state under these unitaries and their inverses, with a target-oriented perturbation towards higher prediction accuracy sandwiched in between. Under reasonable assumptions, we rigorously prove that the evolution converges exponentially to the desired state corresponding to the global minimum of the loss function. We show that such a training process can be understood from the perspective of preparing quantum states by imaginary time evolution, where the data-encoded unitaries together with target-oriented perturbations would train the quantum learning model in an automated fashion. We further prove that the quantum automated learning paradigm features good generalization ability with the generalization error upper bounded by the ratio between a logarithmic function of the Hilbert space dimension and the number of training samples. In addition, we carry out extensive numerical simulations on real-life images and quantum data to demonstrate the effectiveness of our approach and validate the assumptions. Our results establish an unconventional quantum learning strategy that is gradient-free with provable and explainable trainability, which would be crucial for large-scale practical applications of quantum computing in machine learning scenarios.

Expressibility-induced Concentration of Quantum Neural Tangent Kernels

Quantum tangent kernel methods provide an efficient approach to analyzing the performance of quantum machine learning models in the infinite-width limit, which is of crucial importance in designing appropriate circuit architectures for certain learning tasks. Recently, they have been adapted to describe the convergence rate of training errors in quantum neural networks in an analytical manner. Here, we study the connections between the trainability and expressibility of quantum tangent kernel models. In particular, for global loss functions, we rigorously prove that high expressibility of both the global and local quantum encodings can lead to exponential concentration of quantum tangent kernel values to zero. Whereas for local loss functions, such issue of exponential concentration persists owing to the high expressibility, but can be partially mitigated. We further carry out extensive numerical simulations to support our analytical theories. Our discoveries unveil a pivotal characteristic of quantum neural tangent kernels, offering valuable insights for the design of wide quantum variational circuit models in practical applications.

Influenza Modeling Based on Massive Feature Engineering and International Flow Deconvolution

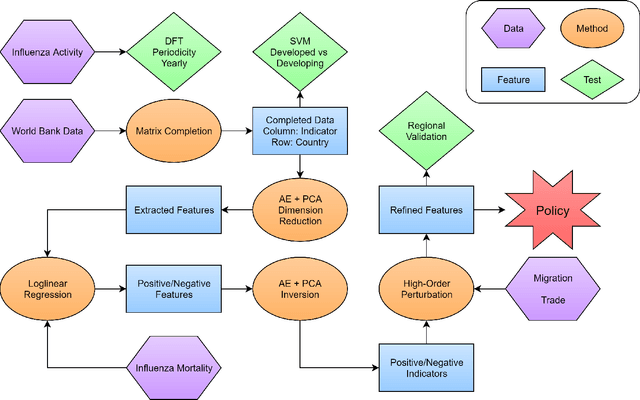
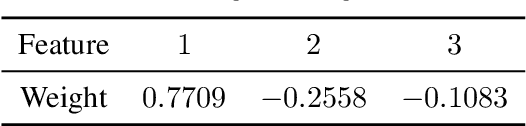
In this article, we focus on the analysis of the potential factors driving the spread of influenza, and possible policies to mitigate the adverse effects of the disease. To be precise, we first invoke discrete Fourier transform (DFT) to conclude a yearly periodic regional structure in the influenza activity, thus safely restricting ourselves to the analysis of the yearly influenza behavior. Then we collect a massive number of possible region-wise indicators contributing to the influenza mortality, such as consumption, immunization, sanitation, water quality, and other indicators from external data, with $1170$ dimensions in total. We extract significant features from the high dimensional indicators using a combination of data analysis techniques, including matrix completion, support vector machines (SVM), autoencoders, and principal component analysis (PCA). Furthermore, we model the international flow of migration and trade as a convolution on regional influenza activity, and solve the deconvolution problem as higher-order perturbations to the linear regression, thus separating regional and international factors related to the influenza mortality. Finally, both the original model and the perturbed model are tested on regional examples, as validations of our models. Pertaining to the policy, we make a proposal based on the connectivity data along with the previously extracted significant features to alleviate the impact of influenza, as well as efficiently propagate and carry out the policies. We conclude that environmental features and economic features are of significance to the influenza mortality. The model can be easily adapted to model other types of infectious diseases.