From Tensor Network Quantum States to Tensorial Recurrent Neural Networks

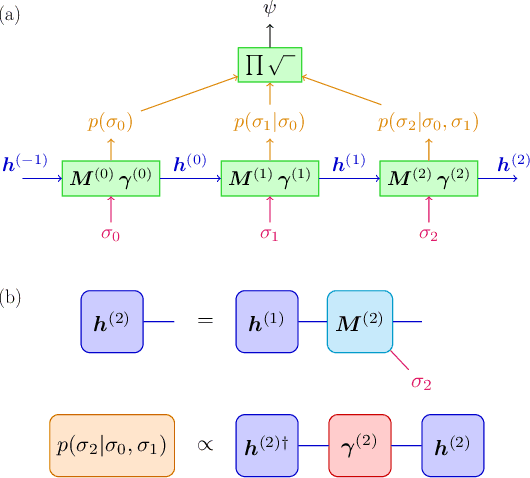
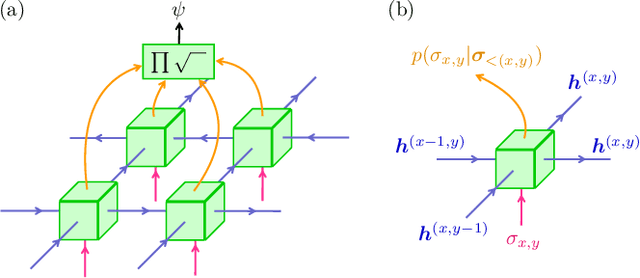
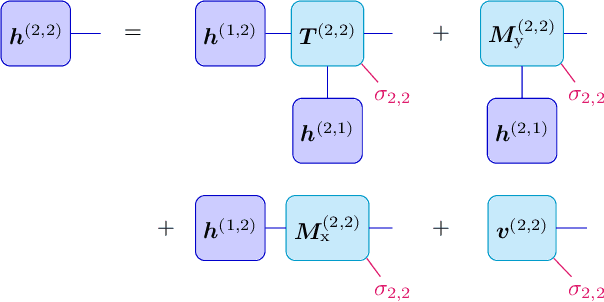
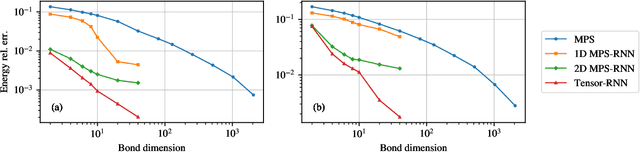
We show that any matrix product state (MPS) can be exactly represented by a recurrent neural network (RNN) with a linear memory update. We generalize this RNN architecture to 2D lattices using a multilinear memory update. It supports perfect sampling and wave function evaluation in polynomial time, and can represent an area law of entanglement entropy. Numerical evidence shows that it can encode the wave function using a bond dimension lower by orders of magnitude when compared to MPS, with an accuracy that can be systematically improved by increasing the bond dimension.

NetKet 3: Machine Learning Toolbox for Many-Body Quantum Systems

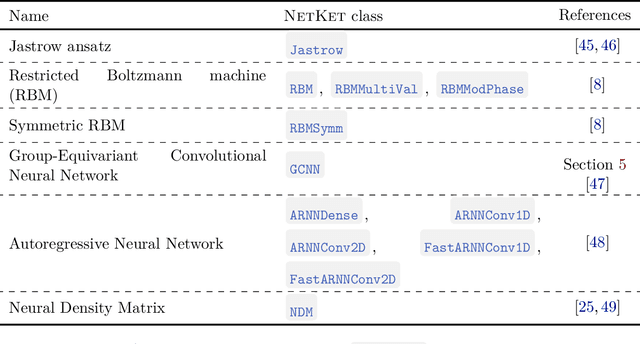
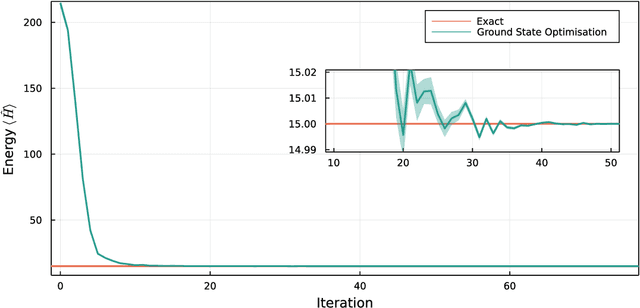
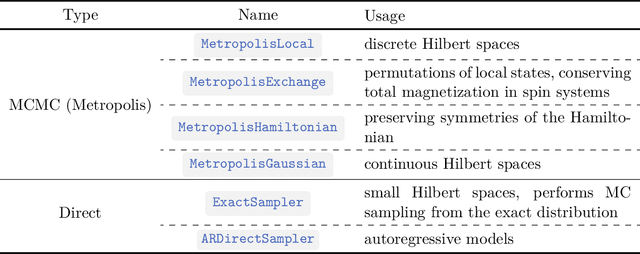
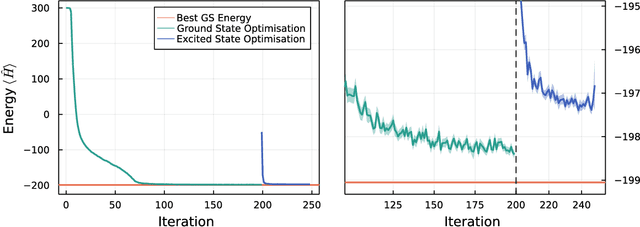
We introduce version 3 of NetKet, the machine learning toolbox for many-body quantum physics. NetKet is built around neural-network quantum states and provides efficient algorithms for their evaluation and optimization. This new version is built on top of JAX, a differentiable programming and accelerated linear algebra framework for the Python programming language. The most significant new feature is the possibility to define arbitrary neural network ans\"atze in pure Python code using the concise notation of machine-learning frameworks, which allows for just-in-time compilation as well as the implicit generation of gradients thanks to automatic differentiation. NetKet 3 also comes with support for GPU and TPU accelerators, advanced support for discrete symmetry groups, chunking to scale up to thousands of degrees of freedom, drivers for quantum dynamics applications, and improved modularity, allowing users to use only parts of the toolbox as a foundation for their own code.

Unbiased Monte Carlo Cluster Updates with Autoregressive Neural Networks

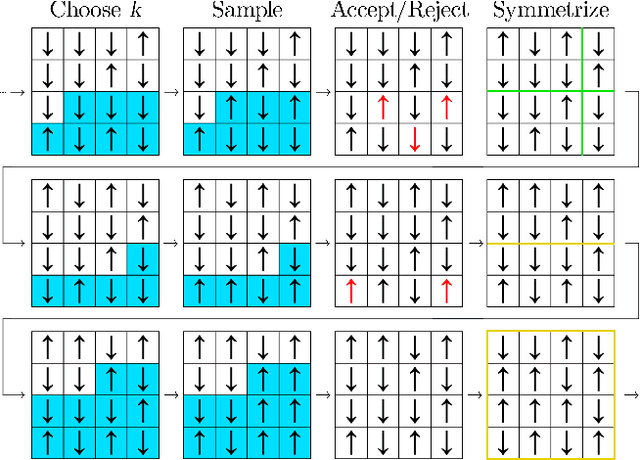
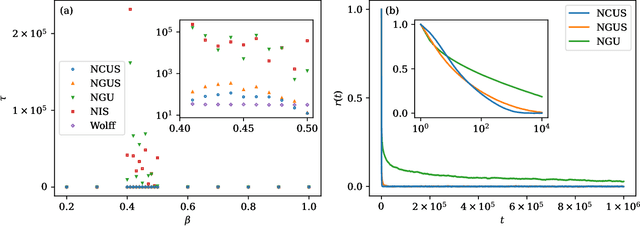
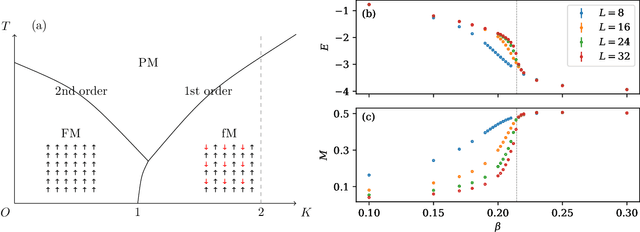
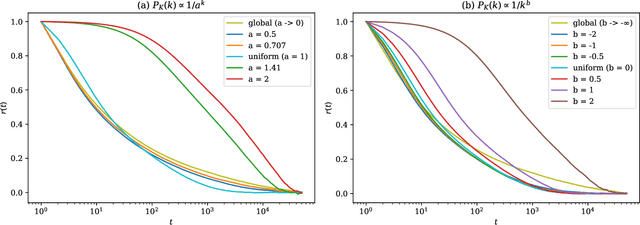
Efficient sampling of complex high-dimensional probability densities is a central task in computational science. Machine Learning techniques based on autoregressive neural networks have been recently shown to provide good approximations of probability distributions of interest in physics. In this work, we propose a systematic way to remove the intrinsic bias associated with these variational approximations, combining it with Markov-chain Monte Carlo in an automatic scheme to efficiently generate cluster updates, which is particularly useful for models for which no efficient cluster update scheme is known. Our approach is based on symmetry-enforced cluster updates building on the neural-network representation of conditional probabilities. We demonstrate that such finite-cluster updates are crucial to circumvent ergodicity problems associated with global neural updates. We test our method for first- and second-order phase transitions in classical spin systems, proving in particular its viability for critical systems, or in the presence of metastable states.

RG-Flow: A hierarchical and explainable flow model based on renormalization group and sparse prior

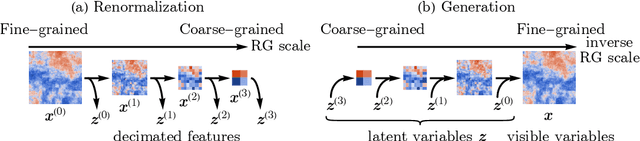
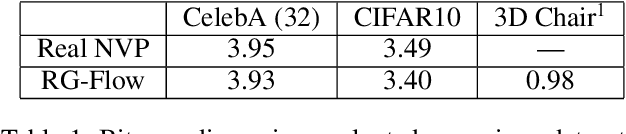
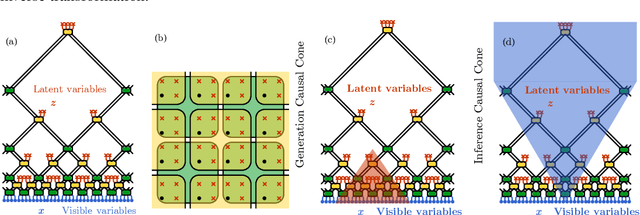
Flow-based generative models have become an important class of unsupervised learning approaches. In this work, we incorporate the key idea of renormalization group (RG) and sparse prior distribution to design a hierarchical flow-based generative model, called RG-Flow, which can separate different scale information of images with disentangle representations at each scale. We demonstrate our method mainly on the CelebA dataset and show that the disentangled representation at different scales enables semantic manipulation and style mixing of the images. To visualize the latent representation, we introduce the receptive fields for flow-based models and find receptive fields learned by RG-Flow are similar to convolutional neural networks. In addition, we replace the widely adopted Gaussian prior distribution by sparse prior distributions to further enhance the disentanglement of representations. From a theoretical perspective, the proposed method has $O(\log L)$ complexity for image inpainting compared to previous flow-based models with $O(L^2)$ complexity.

Influenza Modeling Based on Massive Feature Engineering and International Flow Deconvolution

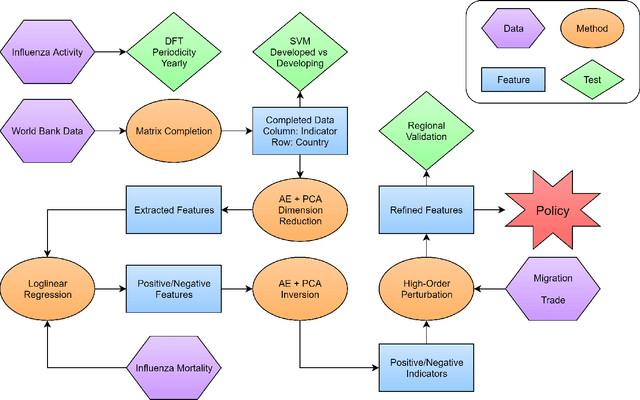
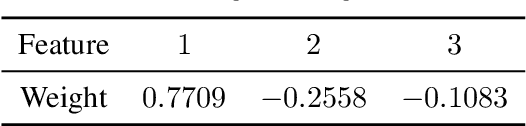
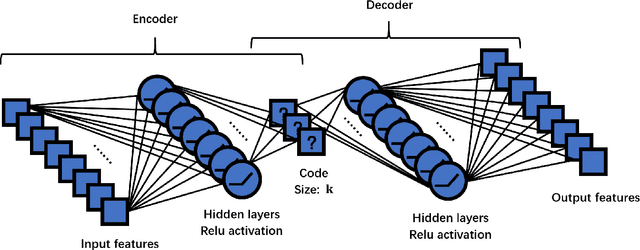
In this article, we focus on the analysis of the potential factors driving the spread of influenza, and possible policies to mitigate the adverse effects of the disease. To be precise, we first invoke discrete Fourier transform (DFT) to conclude a yearly periodic regional structure in the influenza activity, thus safely restricting ourselves to the analysis of the yearly influenza behavior. Then we collect a massive number of possible region-wise indicators contributing to the influenza mortality, such as consumption, immunization, sanitation, water quality, and other indicators from external data, with $1170$ dimensions in total. We extract significant features from the high dimensional indicators using a combination of data analysis techniques, including matrix completion, support vector machines (SVM), autoencoders, and principal component analysis (PCA). Furthermore, we model the international flow of migration and trade as a convolution on regional influenza activity, and solve the deconvolution problem as higher-order perturbations to the linear regression, thus separating regional and international factors related to the influenza mortality. Finally, both the original model and the perturbed model are tested on regional examples, as validations of our models. Pertaining to the policy, we make a proposal based on the connectivity data along with the previously extracted significant features to alleviate the impact of influenza, as well as efficiently propagate and carry out the policies. We conclude that environmental features and economic features are of significance to the influenza mortality. The model can be easily adapted to model other types of infectious diseases.

Solving Statistical Mechanics using Variational Autoregressive Networks

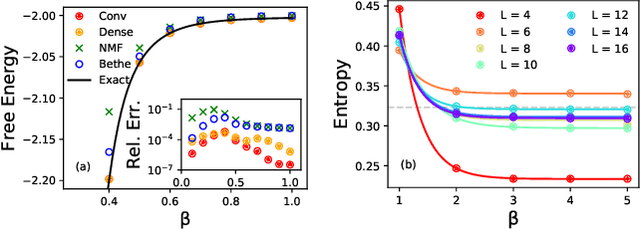
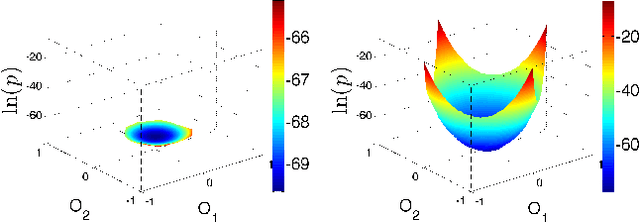
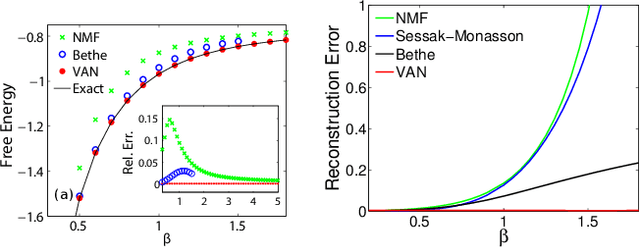
We propose a general framework for solving statistical mechanics of systems with a finite size. The approach extends the celebrated variational mean-field approaches using autoregressive neural networks which support direct sampling and exact calculation of normalized probability of configurations. The network computes variational free energy, estimates physical quantities such as entropy, magnetizations and correlations, and generates uncorrelated samples all at once. Training of the network employs the policy gradient approach in reinforcement learning, which unbiasedly estimates the gradient of variational parameters. We apply our approach to several classical systems, including 2-d Ising models, Hopfield model, Sherrington--Kirkpatrick spin glasses, and the inverse Ising model, for demonstrating its advantages over existing variational mean-field methods. Our approach sheds light on solving statistical physics problems using modern deep generative neural networks.