Solving Statistical Mechanics using Variational Autoregressive Networks

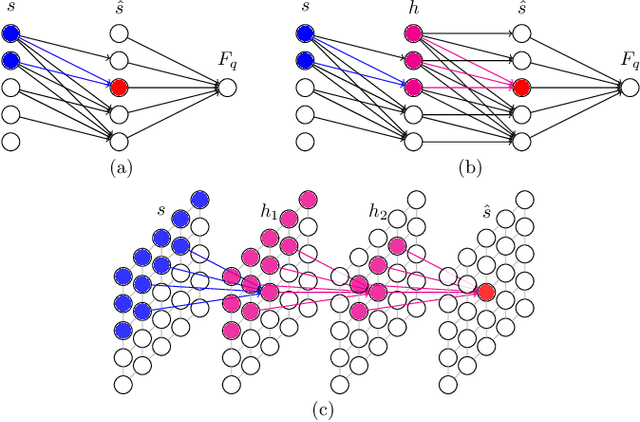
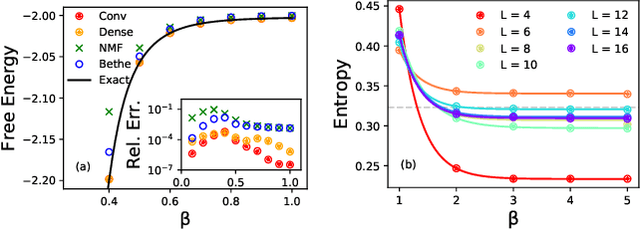
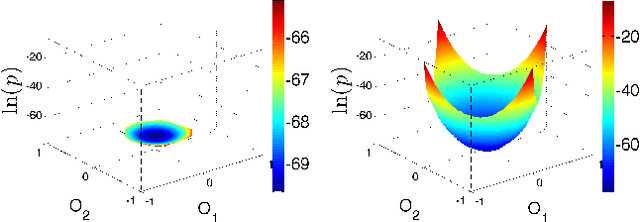
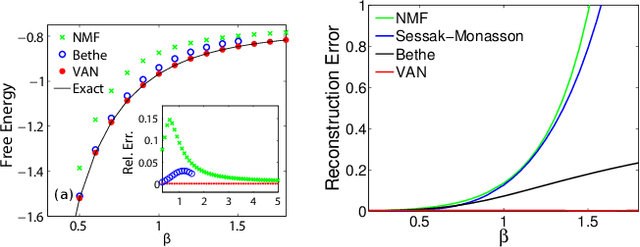
We propose a general framework for solving statistical mechanics of systems with a finite size. The approach extends the celebrated variational mean-field approaches using autoregressive neural networks which support direct sampling and exact calculation of normalized probability of configurations. The network computes variational free energy, estimates physical quantities such as entropy, magnetizations and correlations, and generates uncorrelated samples all at once. Training of the network employs the policy gradient approach in reinforcement learning, which unbiasedly estimates the gradient of variational parameters. We apply our approach to several classical systems, including 2-d Ising models, Hopfield model, Sherrington--Kirkpatrick spin glasses, and the inverse Ising model, for demonstrating its advantages over existing variational mean-field methods. Our approach sheds light on solving statistical physics problems using modern deep generative neural networks.