Learning ground states of gapped quantum Hamiltonians with Kernel Methods

Neural network approaches to approximate the ground state of quantum hamiltonians require the numerical solution of a highly nonlinear optimization problem. We introduce a statistical learning approach that makes the optimization trivial by using kernel methods. Our scheme is an approximate realization of the power method, where supervised learning is used to learn the next step of the power iteration. We show that the ground state properties of arbitrary gapped quantum hamiltonians can be reached with polynomial resources under the assumption that the supervised learning is efficient. Using kernel ridge regression, we provide numerical evidence that the learning assumption is verified by applying our scheme to find the ground states of several prototypical interacting many-body quantum systems, both in one and two dimensions, showing the flexibility of our approach.

Positive-definite parametrization of mixed quantum states with deep neural networks

We introduce the Gram-Hadamard Density Operator (GHDO), a new deep neural-network architecture that can encode positive semi-definite density operators of exponential rank with polynomial resources. We then show how to embed an autoregressive structure in the GHDO to allow direct sampling of the probability distribution. These properties are especially important when representing and variationally optimizing the mixed quantum state of a system interacting with an environment. Finally, we benchmark this architecture by simulating the steady state of the dissipative transverse-field Ising model. Estimating local observables and the R\'enyi entropy, we show significant improvements over previous state-of-the-art variational approaches.

From Tensor Network Quantum States to Tensorial Recurrent Neural Networks

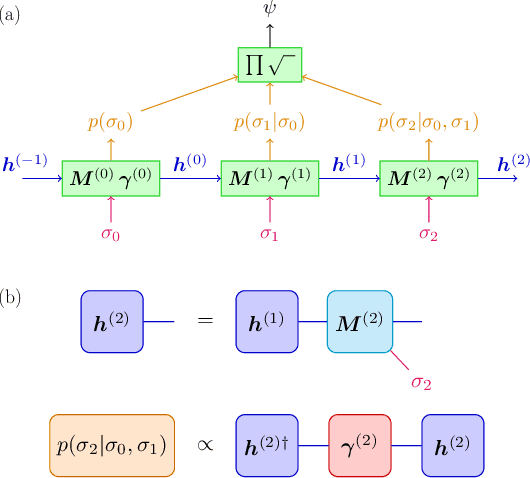
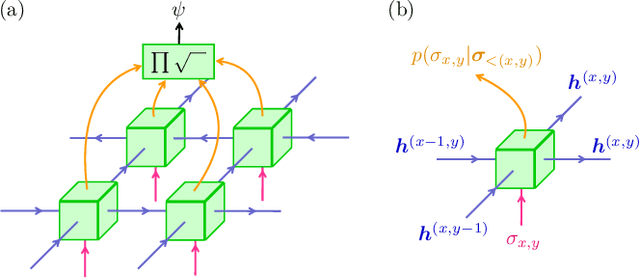
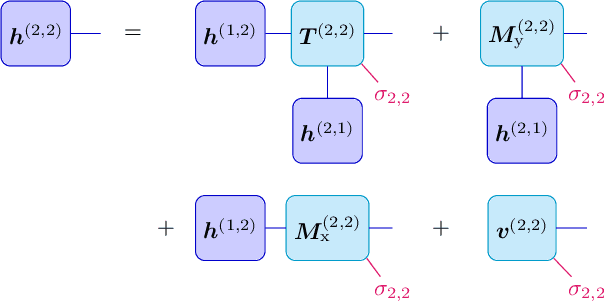
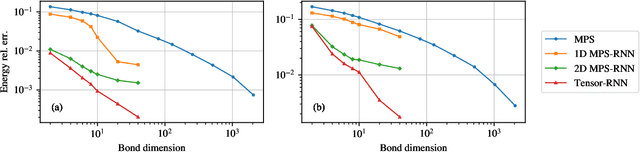
We show that any matrix product state (MPS) can be exactly represented by a recurrent neural network (RNN) with a linear memory update. We generalize this RNN architecture to 2D lattices using a multilinear memory update. It supports perfect sampling and wave function evaluation in polynomial time, and can represent an area law of entanglement entropy. Numerical evidence shows that it can encode the wave function using a bond dimension lower by orders of magnitude when compared to MPS, with an accuracy that can be systematically improved by increasing the bond dimension.

Unbiased Monte Carlo Cluster Updates with Autoregressive Neural Networks

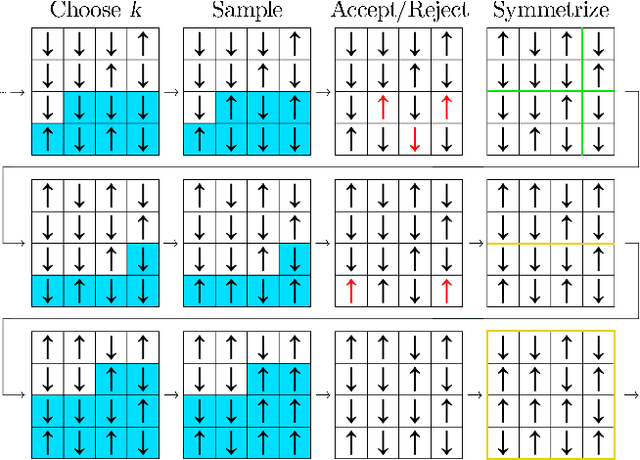
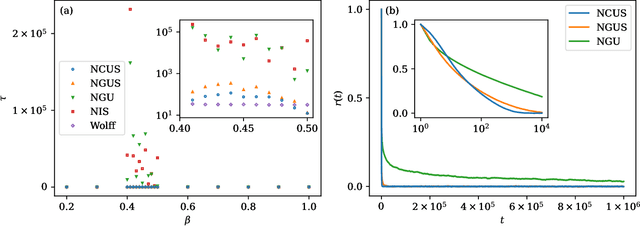
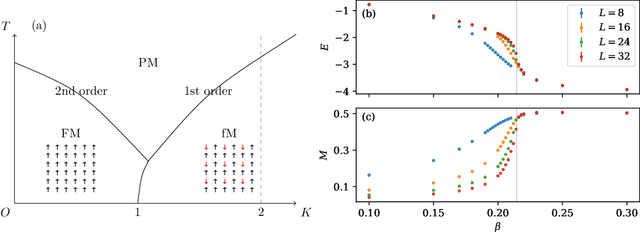
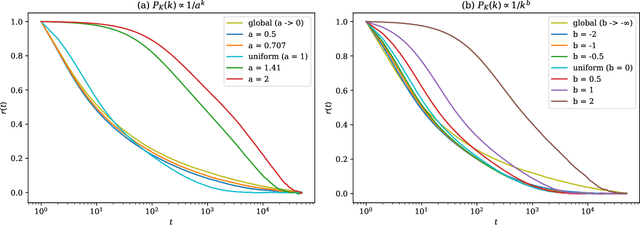
Efficient sampling of complex high-dimensional probability densities is a central task in computational science. Machine Learning techniques based on autoregressive neural networks have been recently shown to provide good approximations of probability distributions of interest in physics. In this work, we propose a systematic way to remove the intrinsic bias associated with these variational approximations, combining it with Markov-chain Monte Carlo in an automatic scheme to efficiently generate cluster updates, which is particularly useful for models for which no efficient cluster update scheme is known. Our approach is based on symmetry-enforced cluster updates building on the neural-network representation of conditional probabilities. We demonstrate that such finite-cluster updates are crucial to circumvent ergodicity problems associated with global neural updates. We test our method for first- and second-order phase transitions in classical spin systems, proving in particular its viability for critical systems, or in the presence of metastable states.

Neural networks trained with WiFi traces to predict airport passenger behavior

The use of neural networks to predict airport passenger activity choices inside the terminal is presented in this paper. Three network architectures are proposed: Feedforward Neural Networks (FNN), Long Short-Term Memory (LSTM) networks, and a combination of the two. Inputs to these models are both static (passenger and trip characteristics) and dynamic (real-time passenger tracking). A real-world case study exemplifies the application of these models, using anonymous WiFi traces collected at Bologna Airport to train the networks. The performance of the models were evaluated according to the misclassification rate of passenger activity choices. In the LSTM approach, two different multi-step forecasting strategies are tested. According to our findings, the direct LSTM approach provides better results than the FNN, especially when the prediction horizon is relatively short (20 minutes or less).