Empirical Sample Complexity of Neural Network Mixed State Reconstruction

Quantum state reconstruction using Neural Quantum States has been proposed as a viable tool to reduce quantum shot complexity in practical applications, and its advantage over competing techniques has been shown in numerical experiments focusing mainly on the noiseless case. In this work, we numerically investigate the performance of different quantum state reconstruction techniques for mixed states: the finite-temperature Ising model. We show how to systematically reduce the quantum resource requirement of the algorithms by applying variance reduction techniques. Then, we compare the two leading neural quantum state encodings of the state, namely, the Neural Density Operator and the positive operator-valued measurement representation, and illustrate their different performance as the mixedness of the target state varies. We find that certain encodings are more efficient in different regimes of mixedness and point out the need for designing more efficient encodings in terms of both classical and quantum resources.

Learning ground states of gapped quantum Hamiltonians with Kernel Methods

Neural network approaches to approximate the ground state of quantum hamiltonians require the numerical solution of a highly nonlinear optimization problem. We introduce a statistical learning approach that makes the optimization trivial by using kernel methods. Our scheme is an approximate realization of the power method, where supervised learning is used to learn the next step of the power iteration. We show that the ground state properties of arbitrary gapped quantum hamiltonians can be reached with polynomial resources under the assumption that the supervised learning is efficient. Using kernel ridge regression, we provide numerical evidence that the learning assumption is verified by applying our scheme to find the ground states of several prototypical interacting many-body quantum systems, both in one and two dimensions, showing the flexibility of our approach.

Positive-definite parametrization of mixed quantum states with deep neural networks

We introduce the Gram-Hadamard Density Operator (GHDO), a new deep neural-network architecture that can encode positive semi-definite density operators of exponential rank with polynomial resources. We then show how to embed an autoregressive structure in the GHDO to allow direct sampling of the probability distribution. These properties are especially important when representing and variationally optimizing the mixed quantum state of a system interacting with an environment. Finally, we benchmark this architecture by simulating the steady state of the dissipative transverse-field Ising model. Estimating local observables and the R\'enyi entropy, we show significant improvements over previous state-of-the-art variational approaches.

From Tensor Network Quantum States to Tensorial Recurrent Neural Networks

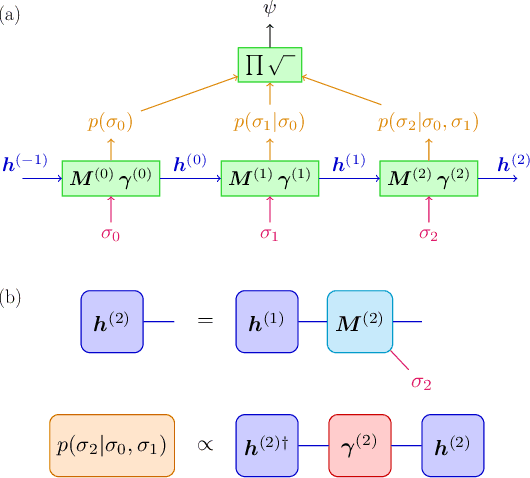
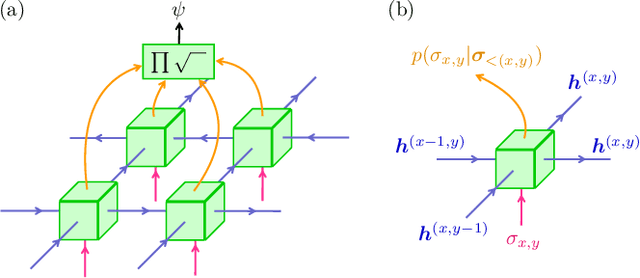
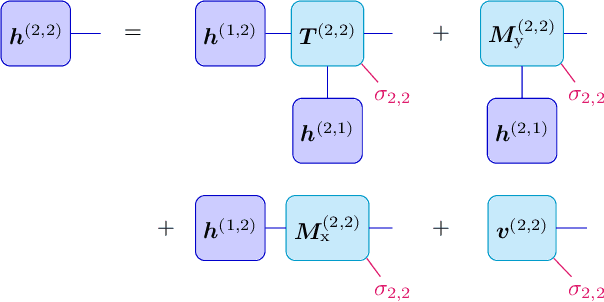
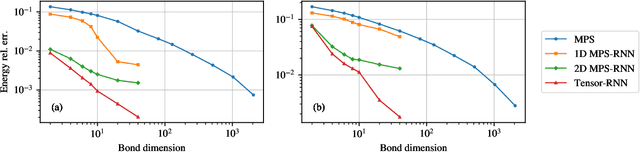
We show that any matrix product state (MPS) can be exactly represented by a recurrent neural network (RNN) with a linear memory update. We generalize this RNN architecture to 2D lattices using a multilinear memory update. It supports perfect sampling and wave function evaluation in polynomial time, and can represent an area law of entanglement entropy. Numerical evidence shows that it can encode the wave function using a bond dimension lower by orders of magnitude when compared to MPS, with an accuracy that can be systematically improved by increasing the bond dimension.

NetKet 3: Machine Learning Toolbox for Many-Body Quantum Systems

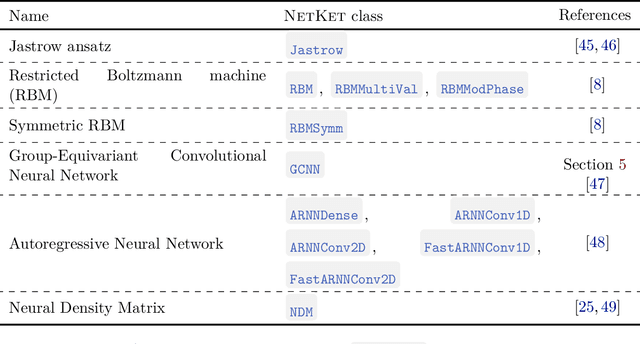
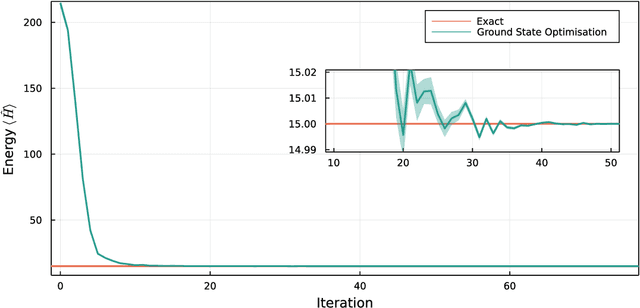
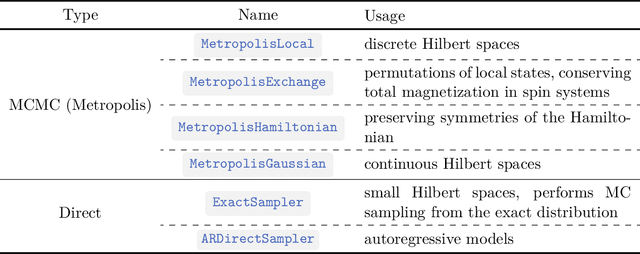
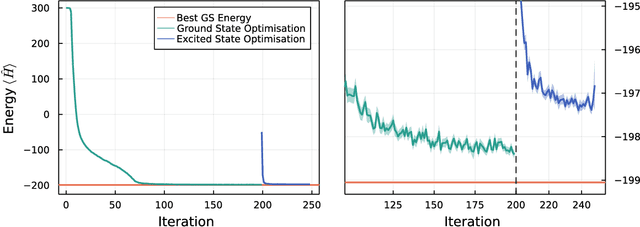
We introduce version 3 of NetKet, the machine learning toolbox for many-body quantum physics. NetKet is built around neural-network quantum states and provides efficient algorithms for their evaluation and optimization. This new version is built on top of JAX, a differentiable programming and accelerated linear algebra framework for the Python programming language. The most significant new feature is the possibility to define arbitrary neural network ans\"atze in pure Python code using the concise notation of machine-learning frameworks, which allows for just-in-time compilation as well as the implicit generation of gradients thanks to automatic differentiation. NetKet 3 also comes with support for GPU and TPU accelerators, advanced support for discrete symmetry groups, chunking to scale up to thousands of degrees of freedom, drivers for quantum dynamics applications, and improved modularity, allowing users to use only parts of the toolbox as a foundation for their own code.