Ansatz-free Hamiltonian learning with Heisenberg-limited scaling

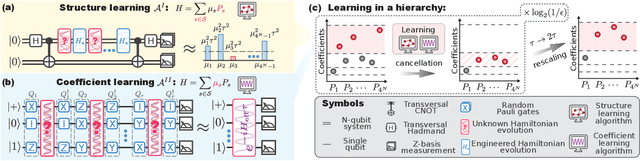
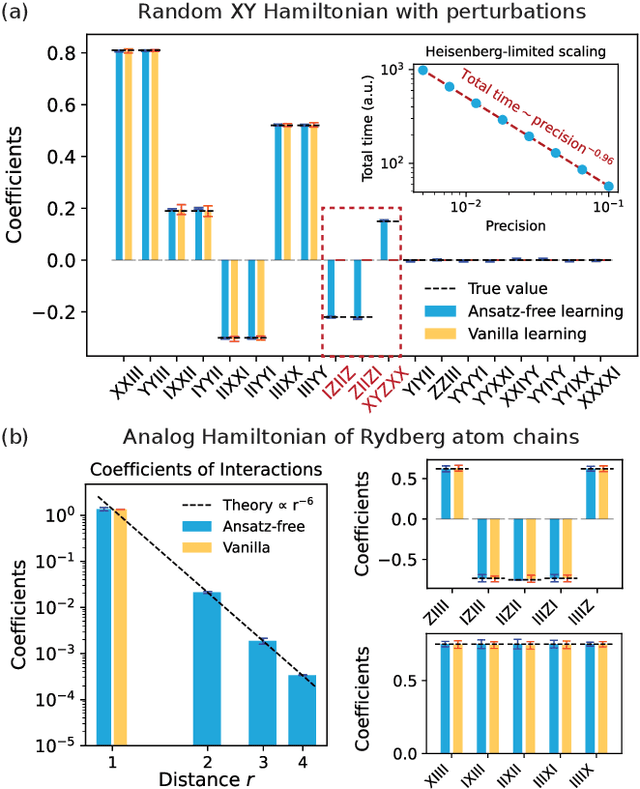
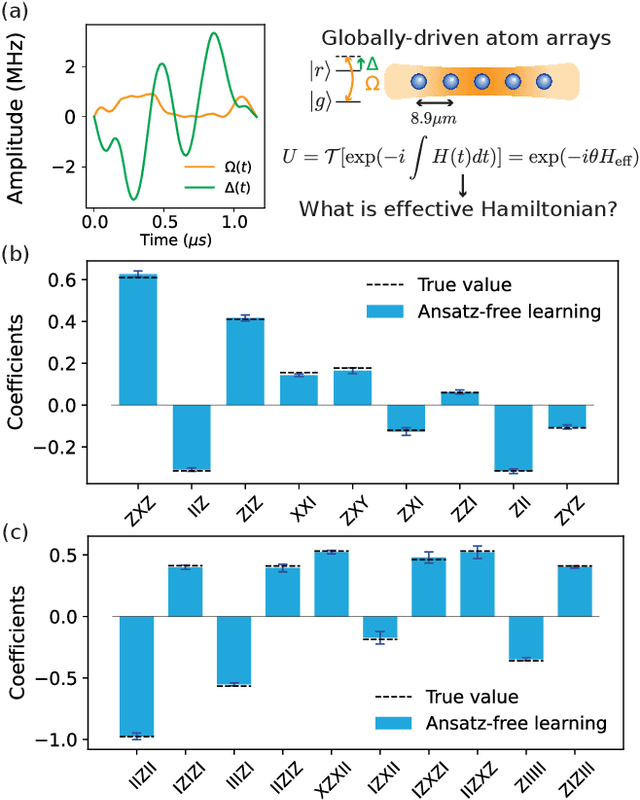
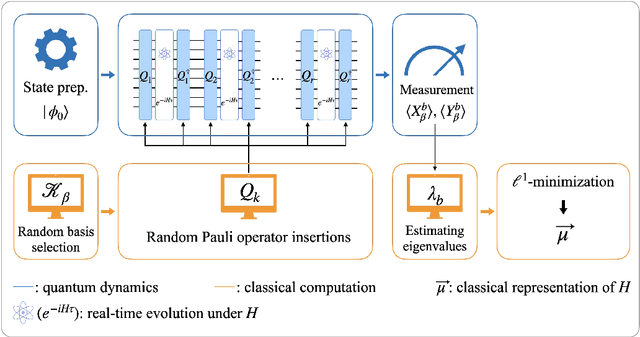
Learning the unknown interactions that govern a quantum system is crucial for quantum information processing, device benchmarking, and quantum sensing. The problem, known as Hamiltonian learning, is well understood under the assumption that interactions are local, but this assumption may not hold for arbitrary Hamiltonians. Previous methods all require high-order inverse polynomial dependency with precision, unable to surpass the standard quantum limit and reach the gold standard Heisenberg-limited scaling. Whether Heisenberg-limited Hamiltonian learning is possible without prior assumptions about the interaction structures, a challenge we term \emph{ansatz-free Hamiltonian learning}, remains an open question. In this work, we present a quantum algorithm to learn arbitrary sparse Hamiltonians without any structure constraints using only black-box queries of the system's real-time evolution and minimal digital controls to attain Heisenberg-limited scaling in estimation error. Our method is also resilient to state-preparation-and-measurement errors, enhancing its practical feasibility. Moreover, we establish a fundamental trade-off between total evolution time and quantum control on learning arbitrary interactions, revealing the intrinsic interplay between controllability and total evolution time complexity for any learning algorithm. These results pave the way for further exploration into Heisenberg-limited Hamiltonian learning in complex quantum systems under minimal assumptions, potentially enabling new benchmarking and verification protocols.

Learning $k$-body Hamiltonians via compressed sensing

We study the problem of learning a $k$-body Hamiltonian with $M$ unknown Pauli terms that are not necessarily geometrically local. We propose a protocol that learns the Hamiltonian to precision $\epsilon$ with total evolution time ${\mathcal{O}}(M^{1/2+1/p}/\epsilon)$ up to logarithmic factors, where the error is quantified by the $\ell^p$-distance between Pauli coefficients. Our learning protocol uses only single-qubit control operations and a GHZ state initial state, is non-adaptive, is robust against SPAM errors, and performs well even if $M$ and $k$ are not precisely known in advance or if the Hamiltonian is not exactly $M$-sparse. Methods from the classical theory of compressed sensing are used for efficiently identifying the $M$ terms in the Hamiltonian from among all possible $k$-body Pauli operators. We also provide a lower bound on the total evolution time needed in this learning task, and we discuss the operational interpretations of the $\ell^1$ and $\ell^2$ error metrics. In contrast to previous works, our learning protocol requires neither geometric locality nor any other relaxed locality conditions.