Active Learning of Quantum System Hamiltonians yields Query Advantage

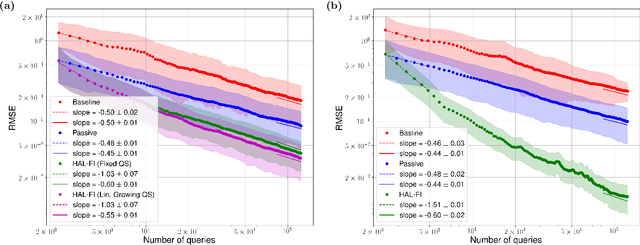
Hamiltonian learning is an important procedure in quantum system identification, calibration, and successful operation of quantum computers. Through queries to the quantum system, this procedure seeks to obtain the parameters of a given Hamiltonian model and description of noise sources. Standard techniques for Hamiltonian learning require careful design of queries and $O(\epsilon^{-2})$ queries in achieving learning error $\epsilon$ due to the standard quantum limit. With the goal of efficiently and accurately estimating the Hamiltonian parameters within learning error $\epsilon$ through minimal queries, we introduce an active learner that is given an initial set of training examples and the ability to interactively query the quantum system to generate new training data. We formally specify and experimentally assess the performance of this Hamiltonian active learning (HAL) algorithm for learning the six parameters of a two-qubit cross-resonance Hamiltonian on four different superconducting IBM Quantum devices. Compared with standard techniques for the same problem and a specified learning error, HAL achieves up to a $99.8\%$ reduction in queries required, and a $99.1\%$ reduction over the comparable non-adaptive learning algorithm. Moreover, with access to prior information on a subset of Hamiltonian parameters and given the ability to select queries with linearly (or exponentially) longer system interaction times during learning, HAL can exceed the standard quantum limit and achieve Heisenberg (or super-Heisenberg) limited convergence rates during learning.

Private learning implies quantum stability

Learning an unknown $n$-qubit quantum state $\rho$ is a fundamental challenge in quantum computing. Information-theoretically, it is known that tomography requires exponential in $n$ many copies of $\rho$ to estimate it up to trace distance. Motivated by computational learning theory, Aaronson et al. introduced many (weaker) learning models: the PAC model of learning states (Proceedings of Royal Society A'07), shadow tomography (STOC'18) for learning "shadows" of a state, a model that also requires learners to be differentially private (STOC'19) and the online model of learning states (NeurIPS'18). In these models it was shown that an unknown state can be learned "approximately" using linear-in-$n$ many copies of rho. But is there any relationship between these models? In this paper we prove a sequence of (information-theoretic) implications from differentially-private PAC learning, to communication complexity, to online learning and then to quantum stability. Our main result generalizes the recent work of Bun, Livni and Moran (Journal of the ACM'21) who showed that finite Littlestone dimension (of Boolean-valued concept classes) implies PAC learnability in the (approximate) differentially private (DP) setting. We first consider their work in the real-valued setting and further extend their techniques to the setting of learning quantum states. Key to our results is our generic quantum online learner, Robust Standard Optimal Algorithm (RSOA), which is robust to adversarial imprecision. We then show information-theoretic implications between DP learning quantum states in the PAC model, learnability of quantum states in the one-way communication model, online learning of quantum states, quantum stability (which is our conceptual contribution), various combinatorial parameters and give further applications to gentle shadow tomography and noisy quantum state learning.

Denoising quantum states with Quantum Autoencoders -- Theory and Applications

We implement a Quantum Autoencoder (QAE) as a quantum circuit capable of correcting Greenberger-Horne-Zeilinger (GHZ) states subject to various noisy quantum channels : the bit-flip channel and the more general quantum depolarizing channel. The QAE shows particularly interesting results, as it enables to perform an almost perfect reconstruction of noisy states, but can also, more surprisingly, act as a generative model to create noise-free GHZ states. Finally, we detail a useful application of QAEs : Quantum Secret Sharing (QSS). We analyze how noise corrupts QSS, causing it to fail, and show how the QAE allows the QSS protocol to succeed even in the presence of noise.