A General Control-Theoretic Approach for Reinforcement Learning: Theory and Algorithms

We devise a control-theoretic reinforcement learning approach to support direct learning of the optimal policy. We establish theoretical properties of our approach and derive an algorithm based on a specific instance of this approach. Our empirical results demonstrate the significant benefits of our approach.

Active Learning of Quantum System Hamiltonians yields Query Advantage

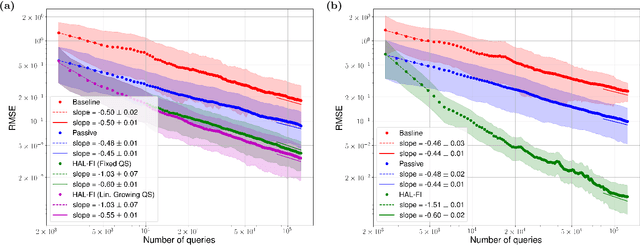
Hamiltonian learning is an important procedure in quantum system identification, calibration, and successful operation of quantum computers. Through queries to the quantum system, this procedure seeks to obtain the parameters of a given Hamiltonian model and description of noise sources. Standard techniques for Hamiltonian learning require careful design of queries and $O(\epsilon^{-2})$ queries in achieving learning error $\epsilon$ due to the standard quantum limit. With the goal of efficiently and accurately estimating the Hamiltonian parameters within learning error $\epsilon$ through minimal queries, we introduce an active learner that is given an initial set of training examples and the ability to interactively query the quantum system to generate new training data. We formally specify and experimentally assess the performance of this Hamiltonian active learning (HAL) algorithm for learning the six parameters of a two-qubit cross-resonance Hamiltonian on four different superconducting IBM Quantum devices. Compared with standard techniques for the same problem and a specified learning error, HAL achieves up to a $99.8\%$ reduction in queries required, and a $99.1\%$ reduction over the comparable non-adaptive learning algorithm. Moreover, with access to prior information on a subset of Hamiltonian parameters and given the ability to select queries with linearly (or exponentially) longer system interaction times during learning, HAL can exceed the standard quantum limit and achieve Heisenberg (or super-Heisenberg) limited convergence rates during learning.

Dither computing: a hybrid deterministic-stochastic computing framework

Stochastic computing has a long history as an alternative method of performing arithmetic on a computer. While it can be considered an unbiased estimator of real numbers, it has a variance and MSE on the order of $\Omega(\frac{1}{N})$. On the other hand, deterministic variants of stochastic computing remove the stochastic aspect, but cannot approximate arbitrary real numbers with arbitrary precision and are biased estimators. However, they have an asymptotically superior MSE on the order of $O(\frac{1}{N^2})$. Recent results in deep learning with stochastic rounding suggest that the bias in the rounding can degrade performance. We proposed an alternative framework, called dither computing, that combines aspects of stochastic computing and its deterministic variants and that can perform computing with similar efficiency, is unbiased, and with a variance and MSE also on the optimal order of $\Theta(\frac{1}{N^2})$. We also show that it can be beneficial in stochastic rounding applications as well. We provide implementation details and give experimental results to comparatively show the benefits of the proposed scheme.

A Control-Model-Based Approach for Reinforcement Learning

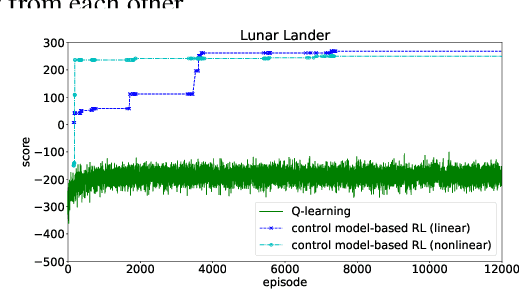
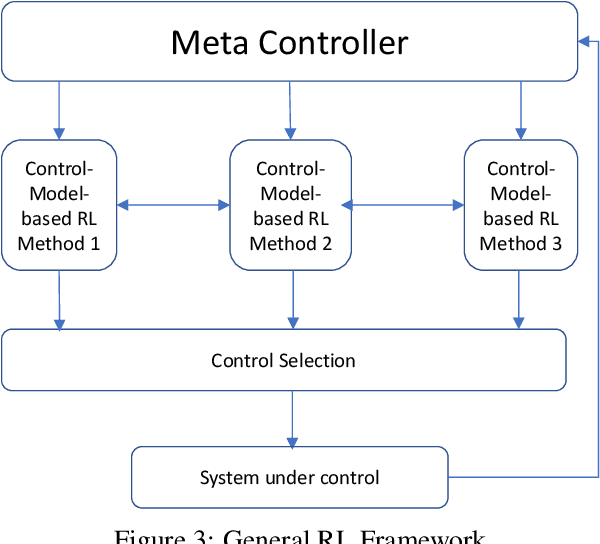
We consider a new form of model-based reinforcement learning methods that directly learns the optimal control parameters, instead of learning the underlying dynamical system. This includes a form of exploration and exploitation in learning and applying the optimal control parameters over time. This also includes a general framework that manages a collection of such control-model-based reinforcement learning methods running in parallel and that selects the best decision from among these parallel methods with the different methods interactively learning together. We derive theoretical results for the optimal control of linear and nonlinear instances of the new control-model-based reinforcement learning methods. Our empirical results demonstrate and quantify the significant benefits of our approach.

LUTNet: speeding up deep neural network inferencing via look-up tables

We consider the use of look-up tables (LUT) to speed up and simplify the hardware implementation of a deep learning network for inferencing after weights have been successfully trained. The use of LUT replaces the matrix multiply and add operations with a small number of LUTs and addition operations resulting in a multiplier-less implementation. We compare the different tradeoffs of this approach in terms of accuracy versus LUT size and the number of operations.

Designing communication systems via iterative improvement: error correction coding with Bayes decoder and codebook optimized for source symbol error

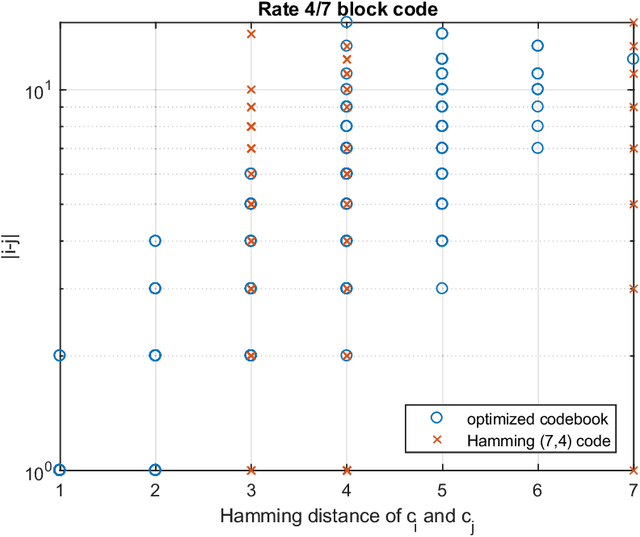
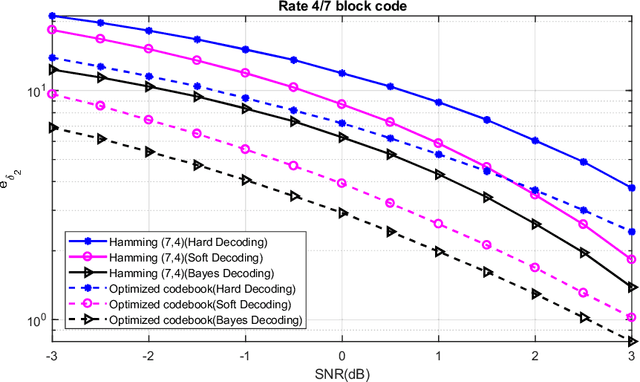
In error correction coding (ECC), the typical error metric is the bit error rate (BER) which measures the number of bit errors. For this metric, the positions of the bits are not relevant to the decoding, and in many noise models, not relevant to the BER either. In many applications this is unsatisfactory as typically all bits are not equal and have different significance. We look at ECC from a Bayesian perspective and introduce Bayes estimators with general loss functions to take into account the bit significance. We propose ECC schemes that optimize this error metric. As the problem is highly nonlinear, traditional ECC construction techniques are not applicable. Using exhausive search is cost prohibitive, and thus we use iterative improvement search techniques to find good codebooks. We provide numerical experiments to show that they can be superior to classical linear block codes such as Hamming codes and decoding methods such as minimum distance decoding.

Can machine learning identify interesting mathematics? An exploration using empirically observed laws

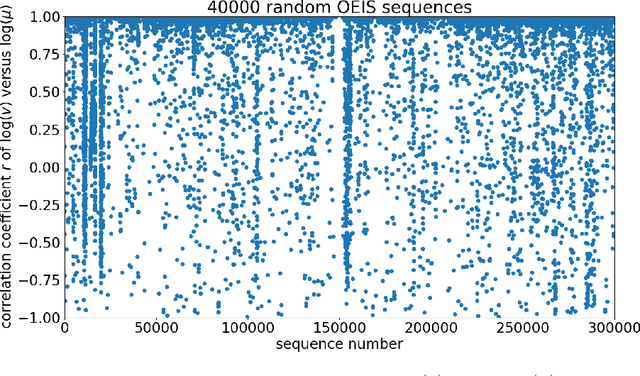
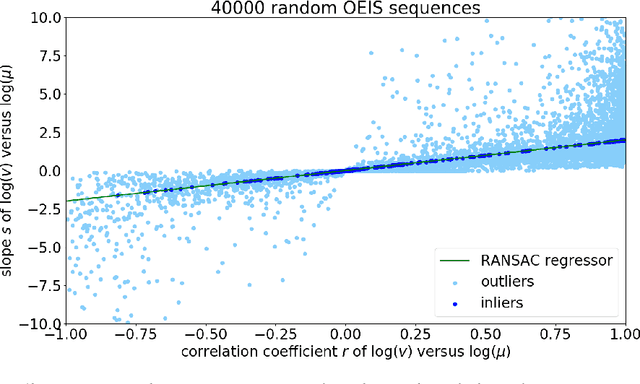
We explore the possibility of using machine learning to identify interesting mathematical structures by using certain quantities that serve as fingerprints. In particular, we extract features from integer sequences using two empirical laws: Benford's law and Taylor's law and experiment with various classifiers to identify whether a sequence is, for example, nice, important, multiplicative, easy to compute or related to primes or palindromes.

ProdSumNet: reducing model parameters in deep neural networks via product-of-sums matrix decompositions

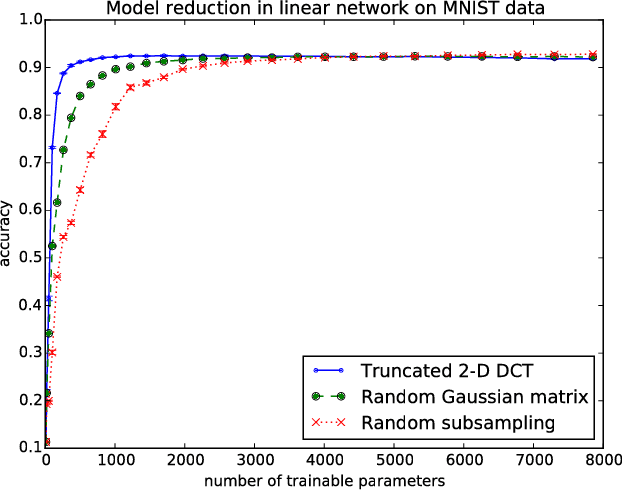
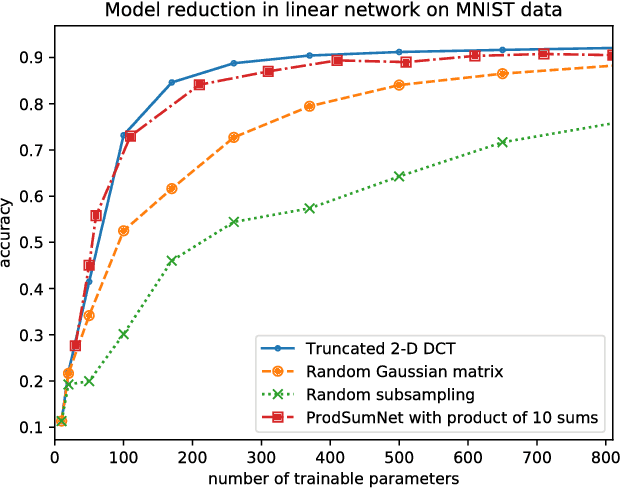
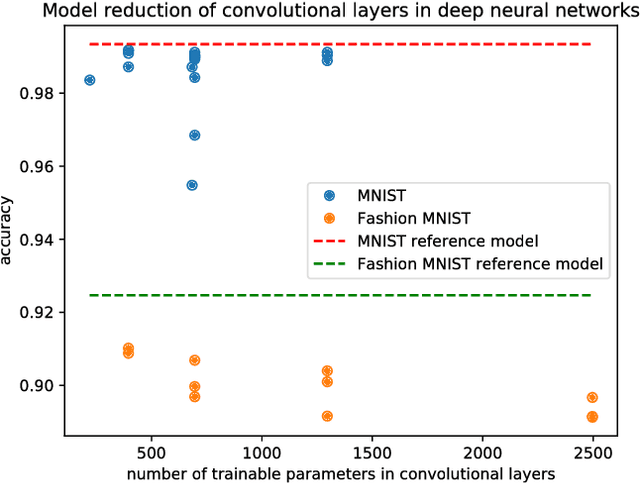
We consider a general framework for reducing the number of trainable model parameters in deep learning networks by decomposing linear operators as a product of sums of simpler linear operators. Recently proposed deep learning architectures such as CNN, KFC, Dilated CNN, etc. are all subsumed in this framework and we illustrate other types of neural network architectures within this framework. We show that good accuracy on MNIST and Fashion MNIST can be obtained using a relatively small number of trainable parameters. In addition, since implementation of the convolutional layer is resource-heavy, we consider an approach in the transform domain that obviates the need for convolutional layers. One of the advantages of this general framework over prior approaches is that the number of trainable parameters is not fixed and can be varied arbitrarily. In particular, we illustrate the tradeoff of varying the number of trainable variables and the corresponding error rate. As an example, by using this decomposition on a reference CNN architecture for MNIST with over 3x10^6 trainable parameters, we are able to obtain an accuracy of 98.44% using only 3554 trainable parameters.

A General Family of Robust Stochastic Operators for Reinforcement Learning

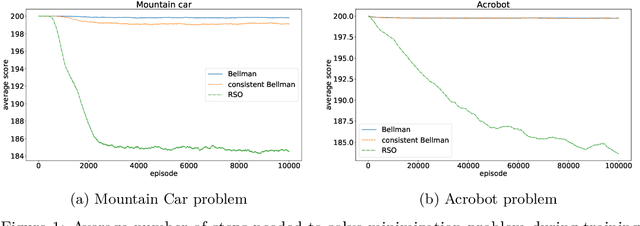
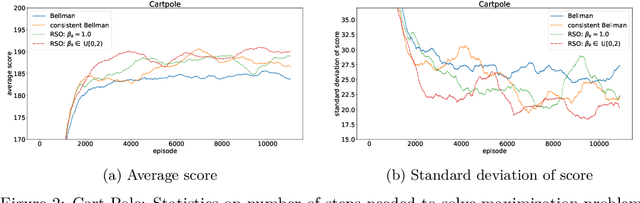
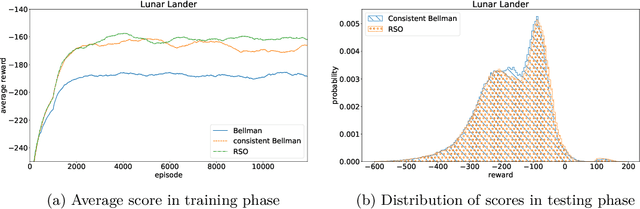
We consider a new family of operators for reinforcement learning with the goal of alleviating the negative effects and becoming more robust to approximation or estimation errors. Various theoretical results are established, which include showing on a sample path basis that our family of operators preserve optimality and increase the action gap. Our empirical results illustrate the strong benefits of our family of operators, significantly outperforming the classical Bellman operator and recently proposed operators.