Toward Mixed Analog-Digital Quantum Signal Processing: Quantum AD/DA Conversion and the Fourier Transform

Signal processing stands as a pillar of classical computation and modern information technology, applicable to both analog and digital signals. Recently, advancements in quantum information science have suggested that quantum signal processing (QSP) can enable more powerful signal processing capabilities. However, the developments in QSP have primarily leveraged \emph{digital} quantum resources, such as discrete-variable (DV) systems like qubits, rather than \emph{analog} quantum resources, such as continuous-variable (CV) systems like quantum oscillators. Consequently, there remains a gap in understanding how signal processing can be performed on hybrid CV-DV quantum computers. Here we address this gap by developing a new paradigm of mixed analog-digital QSP. We demonstrate the utility of this paradigm by showcasing how it naturally enables analog-digital conversion of quantum signals -- specifically, the transfer of states between DV and CV quantum systems. We then show that such quantum analog-digital conversion enables new implementations of quantum algorithms on CV-DV hardware. This is exemplified by realizing the quantum Fourier transform of a state encoded on qubits via the free-evolution of a quantum oscillator, albeit with a runtime exponential in the number of qubits due to information theoretic arguments. Collectively, this work marks a significant step forward in hybrid CV-DV quantum computation, providing a foundation for scalable analog-digital signal processing on quantum processors.

Single-shot Quantum Signal Processing Interferometry

Quantum systems of infinite dimension, such as bosonic oscillators, provide vast resources for quantum sensing. Yet, a general theory on how to manipulate such bosonic modes for sensing beyond parameter estimation is unknown. We present a general algorithmic framework, quantum signal processing interferometry (QSPI), for quantum sensing at the fundamental limits of quantum mechanics, i.e., the Heisenberg sensing limit, by generalizing Ramsey-type interferometry. Our QSPI sensing protocol relies on performing nonlinear polynomial transformations on the oscillator's quadrature operators by generalizing quantum signal processing (QSP) from qubits to hybrid qubit-oscillator systems. We use our QSPI sensing framework to make binary decisions on a displacement channel in the single-shot limit. Theoretical analysis suggests the sensing accuracy given a single-shot qubit measurement can approach the Heisenberg-limit scaling. We further concatenate a series of such binary decisions to perform parameter estimation in a bit-by-bit fashion. Numerical simulations are performed to support these statements. Our QSPI protocol offers a unified framework for quantum sensing using continuous-variable bosonic systems beyond parameter estimation and establishes a promising avenue toward efficient and scalable quantum control and quantum sensing schemes beyond the NISQ era.

Pareto-optimal clustering with the primal deterministic information bottleneck

At the heart of both lossy compression and clustering is a trade-off between the fidelity and size of the learned representation. Our goal is to map out and study the Pareto frontier that quantifies this trade-off. We focus on the Deterministic Information Bottleneck (DIB) formulation of lossy compression, which can be interpreted as a clustering problem. To this end, we introduce the {\it primal} DIB problem, which we show results in a much richer frontier than its previously studied dual counterpart. We present an algorithm for mapping out the Pareto frontier of the primal DIB trade-off that is also applicable to most other two-objective clustering problems. We study general properties of the Pareto frontier, and give both analytic and numerical evidence for logarithmic sparsity of the frontier in general. We provide evidence that our algorithm has polynomial scaling despite the super-exponential search space; and additionally propose a modification to the algorithm that can be used where sampling noise is expected to be significant. Finally, we use our algorithm to map the DIB frontier of three different tasks: compressing the English alphabet, extracting informative color classes from natural images, and compressing a group theory inspired dataset, revealing interesting features of frontier, and demonstrating how the structure of the frontier can be used for model selection with a focus on points previously hidden by the cloak of the convex hull.

Biological error correction codes generate fault-tolerant neural networks

It has been an open question in deep learning if fault-tolerant computation is possible: can arbitrarily reliable computation be achieved using only unreliable neurons? In the mammalian cortex, analog error correction codes known as grid codes have been observed to protect states against neural spiking noise, but their role in information processing is unclear. Here, we use these biological codes to show that a universal fault-tolerant neural network can be achieved if the faultiness of each neuron lies below a sharp threshold, which we find coincides in order of magnitude with noise observed in biological neurons. The discovery of a sharp phase transition from faulty to fault-tolerant neural computation opens a path towards understanding noisy analog systems in artificial intelligence and neuroscience.

Active Learning of Quantum System Hamiltonians yields Query Advantage

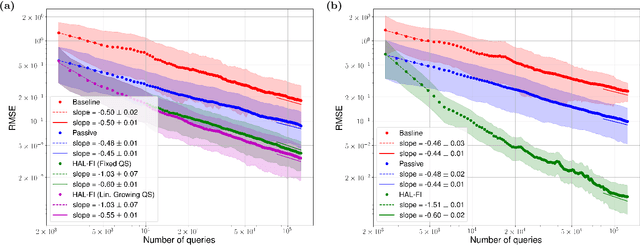
Hamiltonian learning is an important procedure in quantum system identification, calibration, and successful operation of quantum computers. Through queries to the quantum system, this procedure seeks to obtain the parameters of a given Hamiltonian model and description of noise sources. Standard techniques for Hamiltonian learning require careful design of queries and $O(\epsilon^{-2})$ queries in achieving learning error $\epsilon$ due to the standard quantum limit. With the goal of efficiently and accurately estimating the Hamiltonian parameters within learning error $\epsilon$ through minimal queries, we introduce an active learner that is given an initial set of training examples and the ability to interactively query the quantum system to generate new training data. We formally specify and experimentally assess the performance of this Hamiltonian active learning (HAL) algorithm for learning the six parameters of a two-qubit cross-resonance Hamiltonian on four different superconducting IBM Quantum devices. Compared with standard techniques for the same problem and a specified learning error, HAL achieves up to a $99.8\%$ reduction in queries required, and a $99.1\%$ reduction over the comparable non-adaptive learning algorithm. Moreover, with access to prior information on a subset of Hamiltonian parameters and given the ability to select queries with linearly (or exponentially) longer system interaction times during learning, HAL can exceed the standard quantum limit and achieve Heisenberg (or super-Heisenberg) limited convergence rates during learning.

Confident Learning: Estimating Uncertainty in Dataset Labels

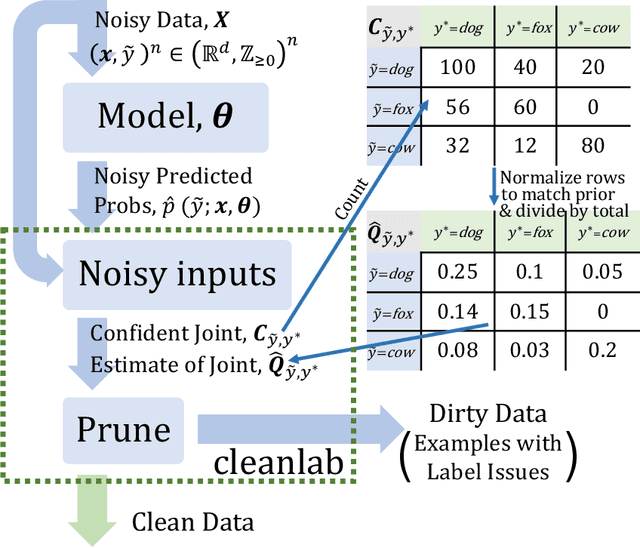
Learning exists in the context of data, yet notions of $\textit{confidence}$ typically focus on model predictions, not label quality. Confident learning (CL) has emerged as an approach for characterizing, identifying, and learning with noisy labels in datasets, based on the principles of pruning noisy data, counting to estimate noise, and ranking examples to train with confidence. Here, we generalize CL, building on the assumption of a classification noise process, to directly estimate the joint distribution between noisy (given) labels and uncorrupted (unknown) labels. This generalized CL, open-sourced as $\texttt{cleanlab}$, is provably consistent under reasonable conditions, and experimentally performant on ImageNet and CIFAR, outperforming recent approaches, e.g. MentorNet, by $30\%$ or more, when label noise is non-uniform. $\texttt{cleanlab}$ also quantifies ontological class overlap, and can increase model accuracy (e.g. ResNet) by providing clean data for training.

Learnability for the Information Bottleneck

The Information Bottleneck (IB) method (\cite{tishby2000information}) provides an insightful and principled approach for balancing compression and prediction for representation learning. The IB objective $I(X;Z)-\beta I(Y;Z)$ employs a Lagrange multiplier $\beta$ to tune this trade-off. However, in practice, not only is $\beta$ chosen empirically without theoretical guidance, there is also a lack of theoretical understanding between $\beta$, learnability, the intrinsic nature of the dataset and model capacity. In this paper, we show that if $\beta$ is improperly chosen, learning cannot happen -- the trivial representation $P(Z|X)=P(Z)$ becomes the global minimum of the IB objective. We show how this can be avoided, by identifying a sharp phase transition between the unlearnable and the learnable which arises as $\beta$ is varied. This phase transition defines the concept of IB-Learnability. We prove several sufficient conditions for IB-Learnability, which provides theoretical guidance for choosing a good $\beta$. We further show that IB-learnability is determined by the largest confident, typical, and imbalanced subset of the examples (the conspicuous subset), and discuss its relation with model capacity. We give practical algorithms to estimate the minimum $\beta$ for a given dataset. We also empirically demonstrate our theoretical conditions with analyses of synthetic datasets, MNIST, and CIFAR10.

Meta-learning autoencoders for few-shot prediction

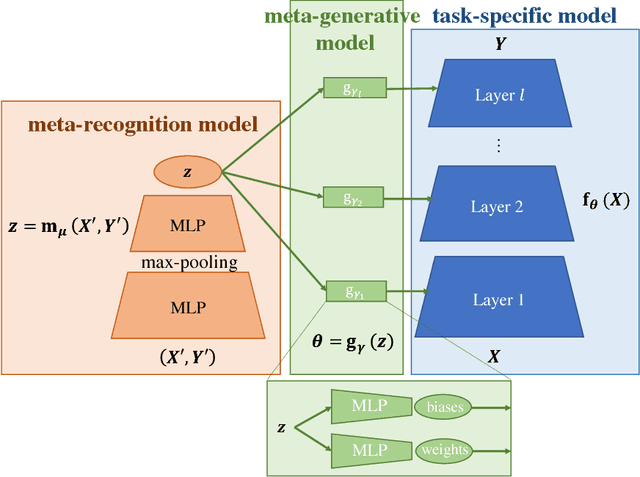
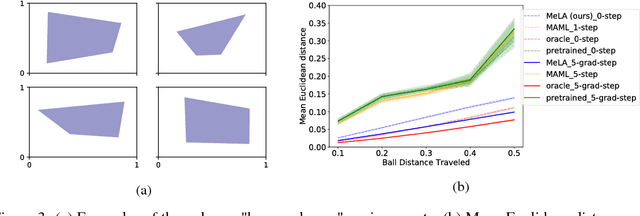
Compared to humans, machine learning models generally require significantly more training examples and fail to extrapolate from experience to solve previously unseen challenges. To help close this performance gap, we augment single-task neural networks with a meta-recognition model which learns a succinct model code via its autoencoder structure, using just a few informative examples. The model code is then employed by a meta-generative model to construct parameters for the task-specific model. We demonstrate that for previously unseen tasks, without additional training, this Meta-Learning Autoencoder (MeLA) framework can build models that closely match the true underlying models, with loss significantly lower than given by fine-tuned baseline networks, and performance that compares favorably with state-of-the-art meta-learning algorithms. MeLA also adds the ability to identify influential training examples and predict which additional data will be most valuable to acquire to improve model prediction.

Learning with Confident Examples: Rank Pruning for Robust Classification with Noisy Labels

Noisy PN learning is the problem of binary classification when training examples may be mislabeled (flipped) uniformly with noise rate rho1 for positive examples and rho0 for negative examples. We propose Rank Pruning (RP) to solve noisy PN learning and the open problem of estimating the noise rates, i.e. the fraction of wrong positive and negative labels. Unlike prior solutions, RP is time-efficient and general, requiring O(T) for any unrestricted choice of probabilistic classifier with T fitting time. We prove RP has consistent noise estimation and equivalent expected risk as learning with uncorrupted labels in ideal conditions, and derive closed-form solutions when conditions are non-ideal. RP achieves state-of-the-art noise estimation and F1, error, and AUC-PR for both MNIST and CIFAR datasets, regardless of the amount of noise and performs similarly impressively when a large portion of training examples are noise drawn from a third distribution. To highlight, RP with a CNN classifier can predict if an MNIST digit is a "one"or "not" with only 0.25% error, and 0.46 error across all digits, even when 50% of positive examples are mislabeled and 50% of observed positive labels are mislabeled negative examples.