Quantum-enhanced Markov chain Monte Carlo

Sampling from complicated probability distributions is a hard computational problem arising in many fields, including statistical physics, optimization, and machine learning. Quantum computers have recently been used to sample from complicated distributions that are hard to sample from classically, but which seldom arise in applications. Here we introduce a quantum algorithm to sample from distributions that pose a bottleneck in several applications, which we implement on a superconducting quantum processor. The algorithm performs Markov chain Monte Carlo (MCMC), a popular iterative sampling technique, to sample from the Boltzmann distribution of classical Ising models. In each step, the quantum processor explores the model in superposition to propose a random move, which is then accepted or rejected by a classical computer and returned to the quantum processor, ensuring convergence to the desired Boltzmann distribution. We find that this quantum algorithm converges in fewer iterations than common classical MCMC alternatives on relevant problem instances, both in simulations and experiments. It therefore opens a new path for quantum computers to solve useful--not merely difficult--problems in the near term.

Active Learning of Quantum System Hamiltonians yields Query Advantage

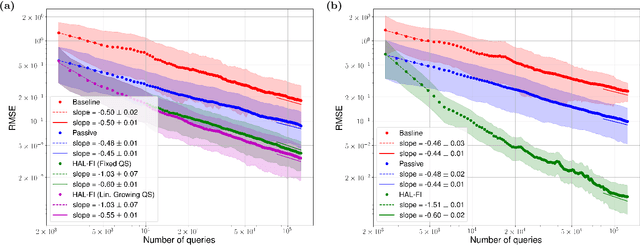
Hamiltonian learning is an important procedure in quantum system identification, calibration, and successful operation of quantum computers. Through queries to the quantum system, this procedure seeks to obtain the parameters of a given Hamiltonian model and description of noise sources. Standard techniques for Hamiltonian learning require careful design of queries and $O(\epsilon^{-2})$ queries in achieving learning error $\epsilon$ due to the standard quantum limit. With the goal of efficiently and accurately estimating the Hamiltonian parameters within learning error $\epsilon$ through minimal queries, we introduce an active learner that is given an initial set of training examples and the ability to interactively query the quantum system to generate new training data. We formally specify and experimentally assess the performance of this Hamiltonian active learning (HAL) algorithm for learning the six parameters of a two-qubit cross-resonance Hamiltonian on four different superconducting IBM Quantum devices. Compared with standard techniques for the same problem and a specified learning error, HAL achieves up to a $99.8\%$ reduction in queries required, and a $99.1\%$ reduction over the comparable non-adaptive learning algorithm. Moreover, with access to prior information on a subset of Hamiltonian parameters and given the ability to select queries with linearly (or exponentially) longer system interaction times during learning, HAL can exceed the standard quantum limit and achieve Heisenberg (or super-Heisenberg) limited convergence rates during learning.