Designing communication systems via iterative improvement: error correction coding with Bayes decoder and codebook optimized for source symbol error

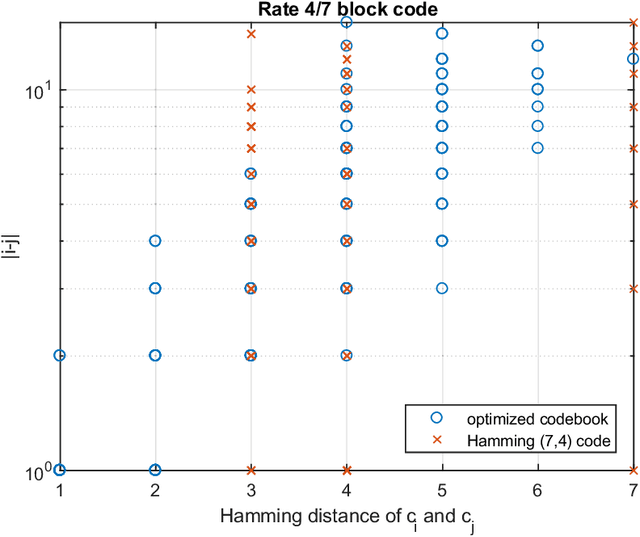
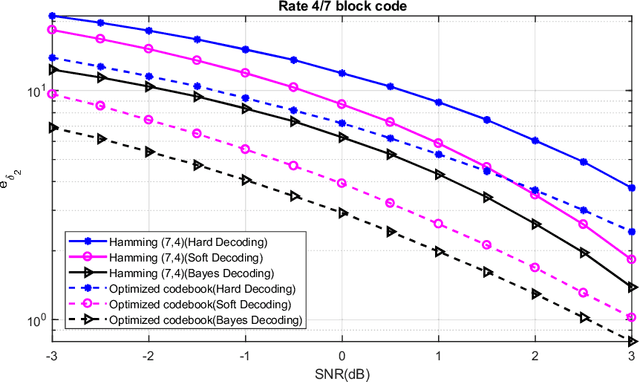
In error correction coding (ECC), the typical error metric is the bit error rate (BER) which measures the number of bit errors. For this metric, the positions of the bits are not relevant to the decoding, and in many noise models, not relevant to the BER either. In many applications this is unsatisfactory as typically all bits are not equal and have different significance. We look at ECC from a Bayesian perspective and introduce Bayes estimators with general loss functions to take into account the bit significance. We propose ECC schemes that optimize this error metric. As the problem is highly nonlinear, traditional ECC construction techniques are not applicable. Using exhausive search is cost prohibitive, and thus we use iterative improvement search techniques to find good codebooks. We provide numerical experiments to show that they can be superior to classical linear block codes such as Hamming codes and decoding methods such as minimum distance decoding.