Can machine learning identify interesting mathematics? An exploration using empirically observed laws
Paper and Code
Sep 10, 2018
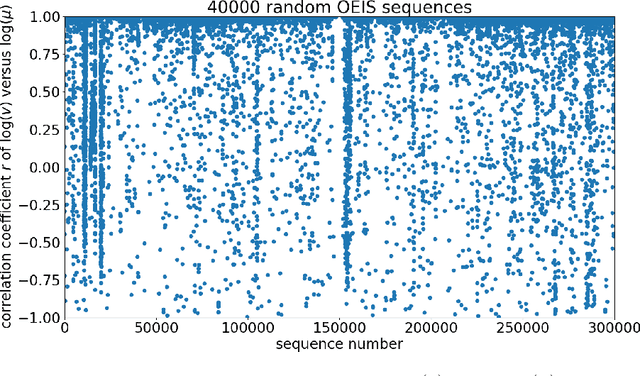
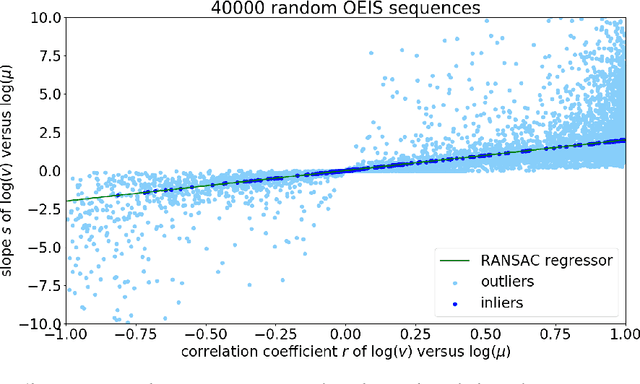
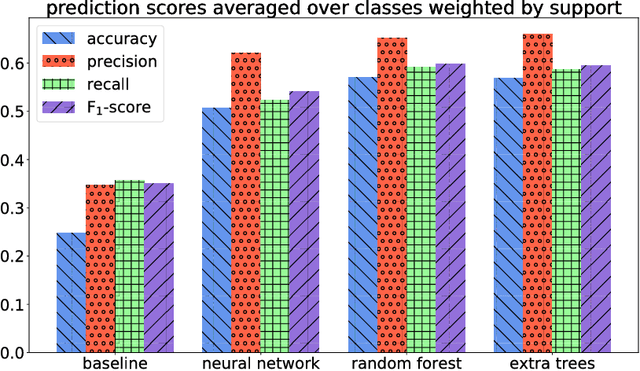
We explore the possibility of using machine learning to identify interesting mathematical structures by using certain quantities that serve as fingerprints. In particular, we extract features from integer sequences using two empirical laws: Benford's law and Taylor's law and experiment with various classifiers to identify whether a sequence is, for example, nice, important, multiplicative, easy to compute or related to primes or palindromes.
* 9 pages, minor edits and fixed typos
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge