ProdSumNet: reducing model parameters in deep neural networks via product-of-sums matrix decompositions
Paper and Code
Sep 06, 2018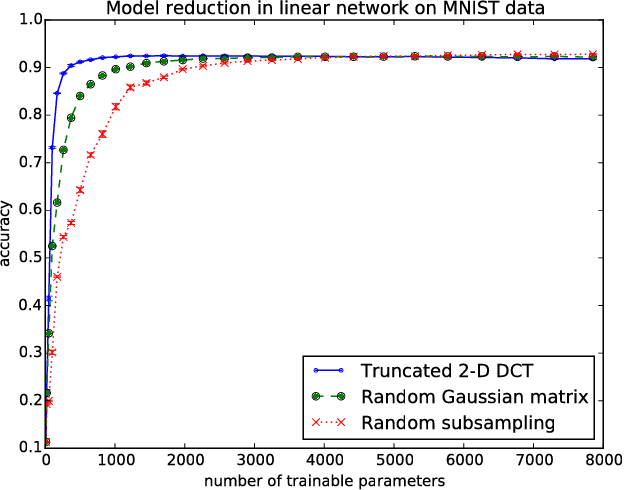

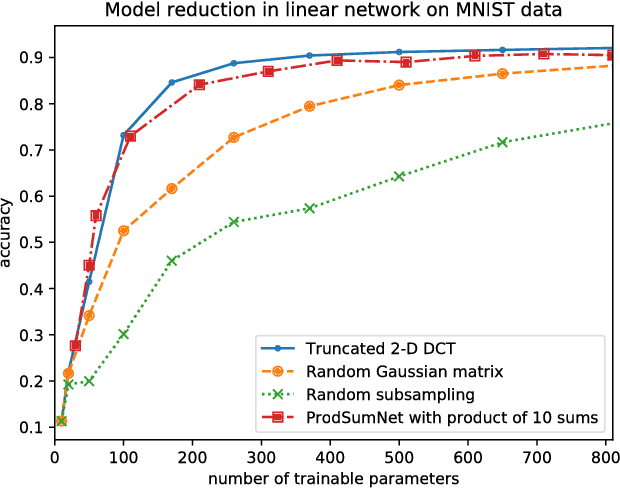
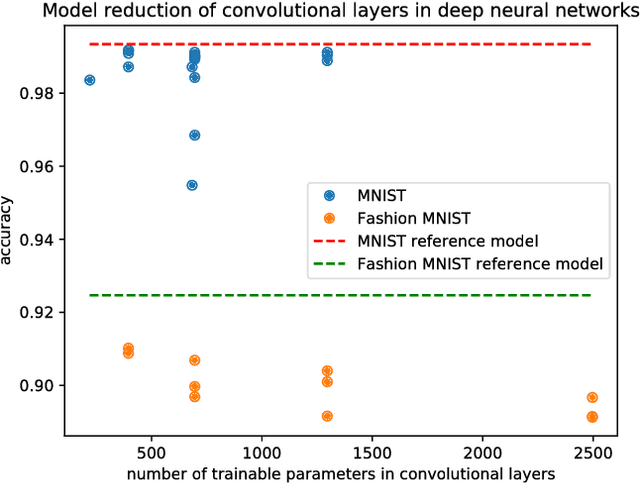
We consider a general framework for reducing the number of trainable model parameters in deep learning networks by decomposing linear operators as a product of sums of simpler linear operators. Recently proposed deep learning architectures such as CNN, KFC, Dilated CNN, etc. are all subsumed in this framework and we illustrate other types of neural network architectures within this framework. We show that good accuracy on MNIST and Fashion MNIST can be obtained using a relatively small number of trainable parameters. In addition, since implementation of the convolutional layer is resource-heavy, we consider an approach in the transform domain that obviates the need for convolutional layers. One of the advantages of this general framework over prior approaches is that the number of trainable parameters is not fixed and can be varied arbitrarily. In particular, we illustrate the tradeoff of varying the number of trainable variables and the corresponding error rate. As an example, by using this decomposition on a reference CNN architecture for MNIST with over 3x10^6 trainable parameters, we are able to obtain an accuracy of 98.44% using only 3554 trainable parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge