A unifying account of warm start guarantees for patches of quantum landscapes

Barren plateaus are fundamentally a statement about quantum loss landscapes on average but there can, and generally will, exist patches of barren plateau landscapes with substantial gradients. Previous work has studied certain classes of parameterized quantum circuits and found example regions where gradients vanish at worst polynomially in system size. Here we present a general bound that unifies all these previous cases and that can tackle physically-motivated ans\"atze that could not be analyzed previously. Concretely, we analytically prove a lower-bound on the variance of the loss that can be used to show that in a non-exponentially narrow region around a point with curvature the loss variance cannot decay exponentially fast. This result is complemented by numerics and an upper-bound that suggest that any loss function with a barren plateau will have exponentially vanishing gradients in any constant radius subregion. Our work thus suggests that while there are hopes to be able to warm-start variational quantum algorithms, any initialization strategy that cannot get increasingly close to the region of attraction with increasing problem size is likely inadequate.

Efficient quantum-enhanced classical simulation for patches of quantum landscapes

Understanding the capabilities of classical simulation methods is key to identifying where quantum computers are advantageous. Not only does this ensure that quantum computers are used only where necessary, but also one can potentially identify subroutines that can be offloaded onto a classical device. In this work, we show that it is always possible to generate a classical surrogate of a sub-region (dubbed a "patch") of an expectation landscape produced by a parameterized quantum circuit. That is, we provide a quantum-enhanced classical algorithm which, after simple measurements on a quantum device, allows one to classically simulate approximate expectation values of a subregion of a landscape. We provide time and sample complexity guarantees for a range of families of circuits of interest, and further numerically demonstrate our simulation algorithms on an exactly verifiable simulation of a Hamiltonian variational ansatz and long-time dynamics simulation on a 127-qubit heavy-hex topology.

Quantum Convolutional Neural Networks are (Effectively) Classically Simulable

Quantum Convolutional Neural Networks (QCNNs) are widely regarded as a promising model for Quantum Machine Learning (QML). In this work we tie their heuristic success to two facts. First, that when randomly initialized, they can only operate on the information encoded in low-bodyness measurements of their input states. And second, that they are commonly benchmarked on "locally-easy'' datasets whose states are precisely classifiable by the information encoded in these low-bodyness observables subspace. We further show that the QCNN's action on this subspace can be efficiently classically simulated by a classical algorithm equipped with Pauli shadows on the dataset. Indeed, we present a shadow-based simulation of QCNNs on up-to $1024$ qubits for phases of matter classification. Our results can then be understood as highlighting a deeper symptom of QML: Models could only be showing heuristic success because they are benchmarked on simple problems, for which their action can be classically simulated. This insight points to the fact that non-trivial datasets are a truly necessary ingredient for moving forward with QML. To finish, we discuss how our results can be extrapolated to classically simulate other architectures.

Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing

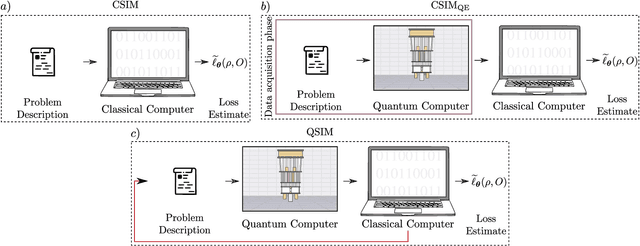
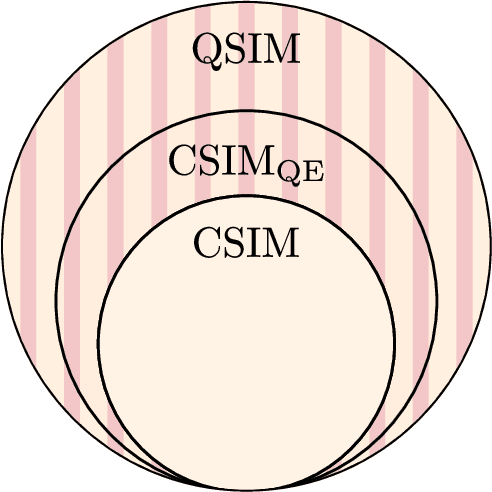
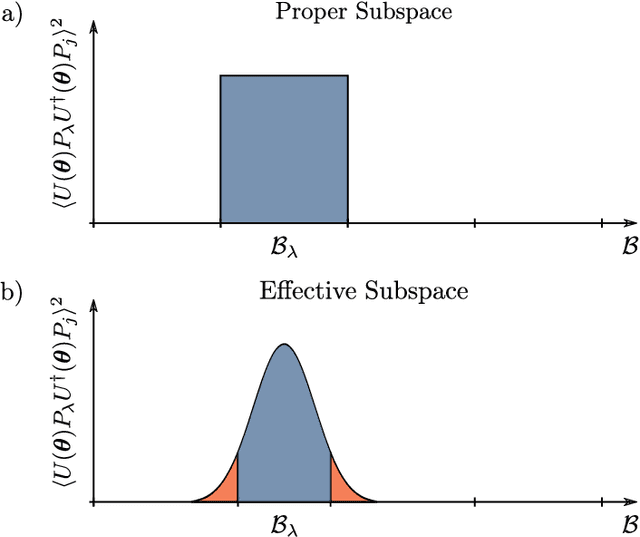
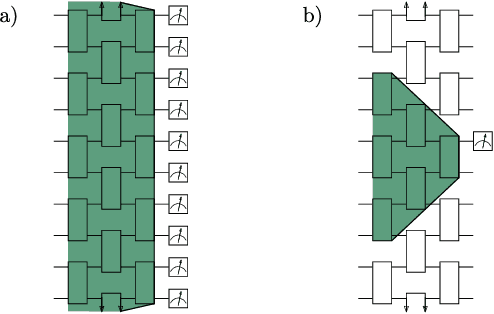
A large amount of effort has recently been put into understanding the barren plateau phenomenon. In this perspective article, we face the increasingly loud elephant in the room and ask a question that has been hinted at by many but not explicitly addressed: Can the structure that allows one to avoid barren plateaus also be leveraged to efficiently simulate the loss classically? We present strong evidence that commonly used models with provable absence of barren plateaus are also classically simulable, provided that one can collect some classical data from quantum devices during an initial data acquisition phase. This follows from the observation that barren plateaus result from a curse of dimensionality, and that current approaches for solving them end up encoding the problem into some small, classically simulable, subspaces. This sheds serious doubt on the non-classicality of the information processing capabilities of parametrized quantum circuits for barren plateau-free landscapes and on the possibility of superpolynomial advantages from running them on quantum hardware. We end by discussing caveats in our arguments, the role of smart initializations, and by highlighting new opportunities that our perspective raises.

Trainability barriers and opportunities in quantum generative modeling

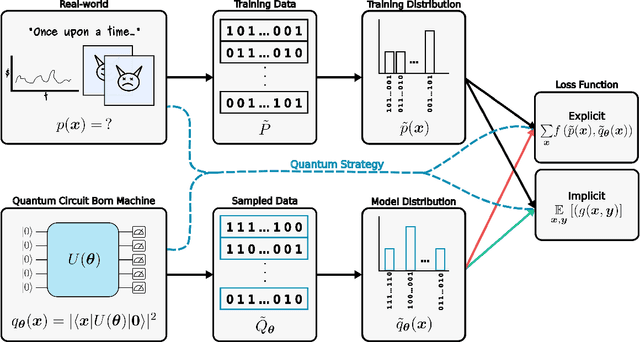
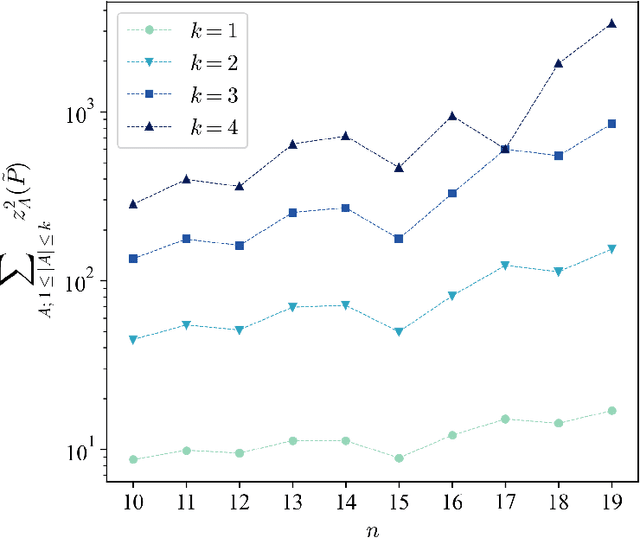
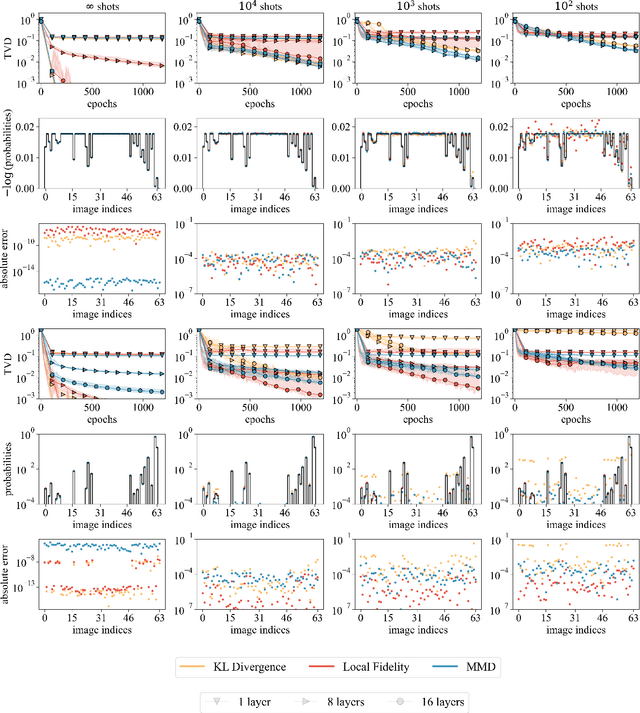
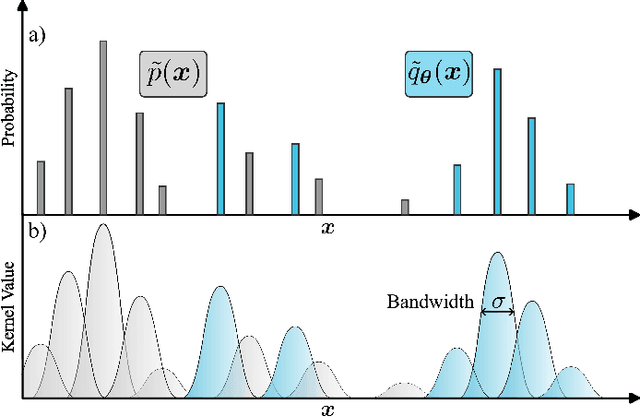
Quantum generative models, in providing inherently efficient sampling strategies, show promise for achieving a near-term advantage on quantum hardware. Nonetheless, important questions remain regarding their scalability. In this work, we investigate the barriers to the trainability of quantum generative models posed by barren plateaus and exponential loss concentration. We explore the interplay between explicit and implicit models and losses, and show that using implicit generative models (such as quantum circuit-based models) with explicit losses (such as the KL divergence) leads to a new flavour of barren plateau. In contrast, the Maximum Mean Discrepancy (MMD), which is a popular example of an implicit loss, can be viewed as the expectation value of an observable that is either low-bodied and trainable, or global and untrainable depending on the choice of kernel. However, in parallel, we highlight that the low-bodied losses required for trainability cannot in general distinguish high-order correlations, leading to a fundamental tension between exponential concentration and the emergence of spurious minima. We further propose a new local quantum fidelity-type loss which, by leveraging quantum circuits to estimate the quality of the encoded distribution, is both faithful and enjoys trainability guarantees. Finally, we compare the performance of different loss functions for modelling real-world data from the High-Energy-Physics domain and confirm the trends predicted by our theoretical results.

The power and limitations of learning quantum dynamics incoherently

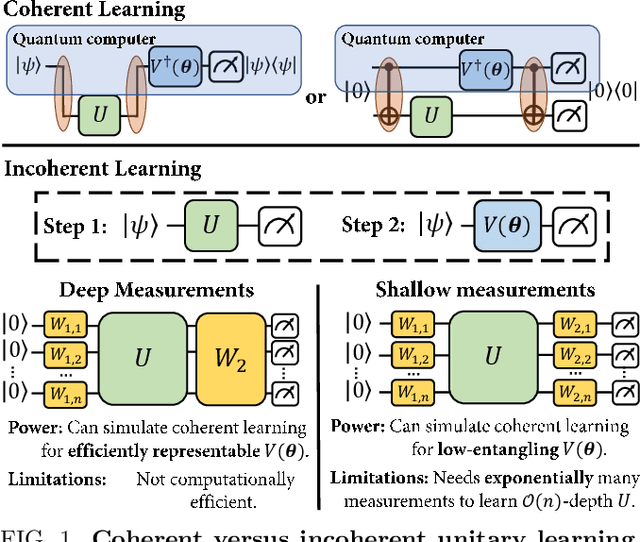
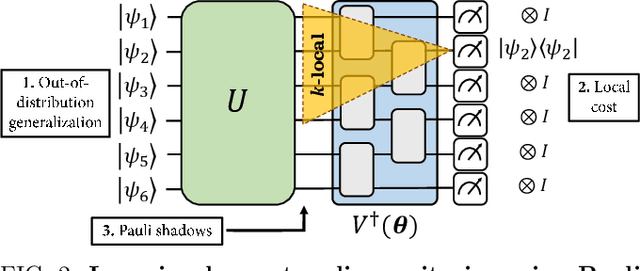
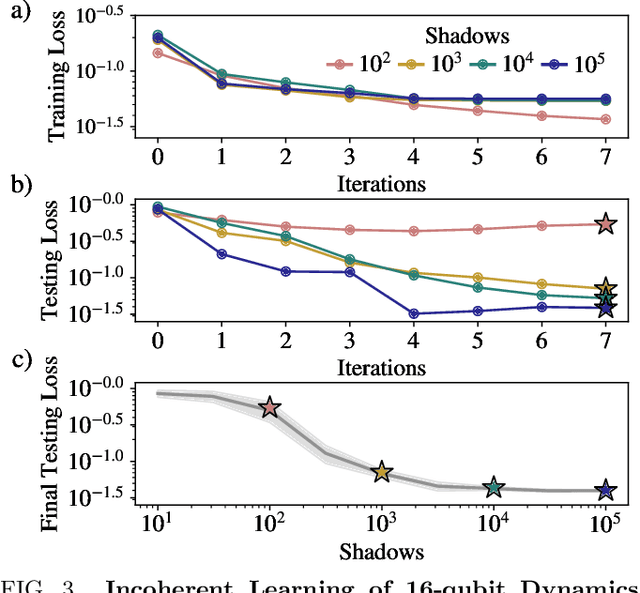
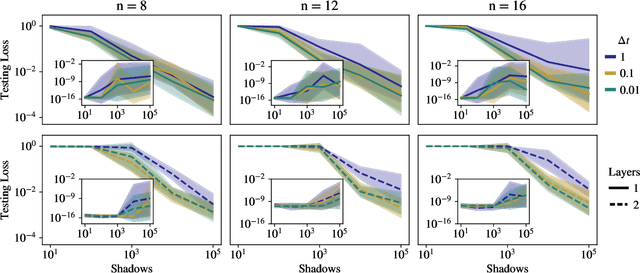
Quantum process learning is emerging as an important tool to study quantum systems. While studied extensively in coherent frameworks, where the target and model system can share quantum information, less attention has been paid to whether the dynamics of quantum systems can be learned without the system and target directly interacting. Such incoherent frameworks are practically appealing since they open up methods of transpiling quantum processes between the different physical platforms without the need for technically challenging hybrid entanglement schemes. Here we provide bounds on the sample complexity of learning unitary processes incoherently by analyzing the number of measurements that are required to emulate well-established coherent learning strategies. We prove that if arbitrary measurements are allowed, then any efficiently representable unitary can be efficiently learned within the incoherent framework; however, when restricted to shallow-depth measurements only low-entangling unitaries can be learned. We demonstrate our incoherent learning algorithm for low entangling unitaries by successfully learning a 16-qubit unitary on \texttt{ibmq\_kolkata}, and further demonstrate the scalabilty of our proposed algorithm through extensive numerical experiments.