Guided Quantum Compression for Higgs Identification

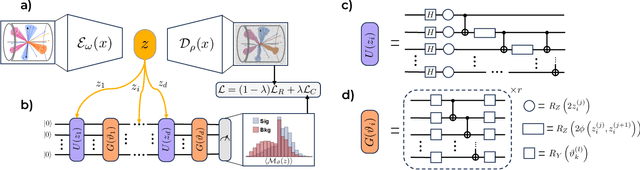
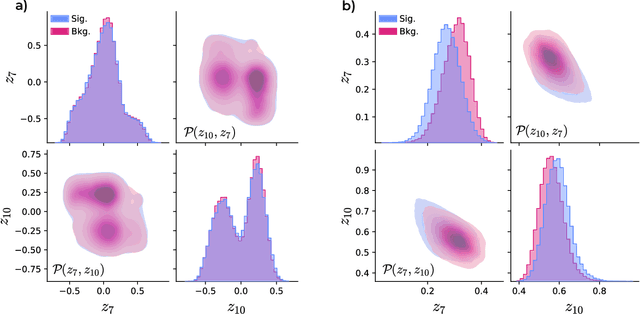
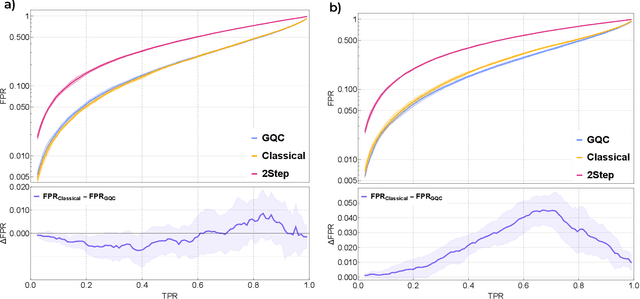
Quantum machine learning provides a fundamentally novel and promising approach to analyzing data. However, many data sets are too complex for currently available quantum computers. Consequently, quantum machine learning applications conventionally resort to dimensionality reduction algorithms, e.g., auto-encoders, before passing data through the quantum models. We show that using a classical auto-encoder as an independent preprocessing step can significantly decrease the classification performance of a quantum machine learning algorithm. To ameliorate this issue, we design an architecture that unifies the preprocessing and quantum classification algorithms into a single trainable model: the guided quantum compression model. The utility of this model is demonstrated by using it to identify the Higgs boson in proton-proton collisions at the LHC, where the conventional approach proves ineffective. Conversely, the guided quantum compression model excels at solving this classification problem, achieving a good accuracy. Additionally, the model developed herein shows better performance compared to the classical benchmark when using only low-level kinematic features.

Symmetry breaking in geometric quantum machine learning in the presence of noise

Geometric quantum machine learning based on equivariant quantum neural networks (EQNN) recently appeared as a promising direction in quantum machine learning. Despite the encouraging progress, the studies are still limited to theory, and the role of hardware noise in EQNN training has never been explored. This work studies the behavior of EQNN models in the presence of noise. We show that certain EQNN models can preserve equivariance under Pauli channels, while this is not possible under the amplitude damping channel. We claim that the symmetry breaking grows linearly in the number of layers and noise strength. We support our claims with numerical data from simulations as well as hardware up to 64 qubits. Furthermore, we provide strategies to enhance the symmetry protection of EQNN models in the presence of noise.

Approximately Equivariant Quantum Neural Network for $p4m$ Group Symmetries in Images

Quantum Neural Networks (QNNs) are suggested as one of the quantum algorithms which can be efficiently simulated with a low depth on near-term quantum hardware in the presence of noises. However, their performance highly relies on choosing the most suitable architecture of Variational Quantum Algorithms (VQAs), and the problem-agnostic models often suffer issues regarding trainability and generalization power. As a solution, the most recent works explore Geometric Quantum Machine Learning (GQML) using QNNs equivariant with respect to the underlying symmetry of the dataset. GQML adds an inductive bias to the model by incorporating the prior knowledge on the given dataset and leads to enhancing the optimization performance while constraining the search space. This work proposes equivariant Quantum Convolutional Neural Networks (EquivQCNNs) for image classification under planar $p4m$ symmetry, including reflectional and $90^\circ$ rotational symmetry. We present the results tested in different use cases, such as phase detection of the 2D Ising model and classification of the extended MNIST dataset, and compare them with those obtained with the non-equivariant model, proving that the equivariance fosters better generalization of the model.

Hybrid Ground-State Quantum Algorithms based on Neural Schrödinger Forging

Entanglement forging based variational algorithms leverage the bi-partition of quantum systems for addressing ground state problems. The primary limitation of these approaches lies in the exponential summation required over the numerous potential basis states, or bitstrings, when performing the Schmidt decomposition of the whole system. To overcome this challenge, we propose a new method for entanglement forging employing generative neural networks to identify the most pertinent bitstrings, eliminating the need for the exponential sum. Through empirical demonstrations on systems of increasing complexity, we show that the proposed algorithm achieves comparable or superior performance compared to the existing standard implementation of entanglement forging. Moreover, by controlling the amount of required resources, this scheme can be applied to larger, as well as non permutation invariant systems, where the latter constraint is associated with the Heisenberg forging procedure. We substantiate our findings through numerical simulations conducted on spins models exhibiting one-dimensional ring, two-dimensional triangular lattice topologies, and nuclear shell model configurations.

Assessment of few-hits machine learning classification algorithms for low energy physics in liquid argon detectors

The physics potential of massive liquid argon TPCs in the low-energy regime is still to be fully reaped because few-hits events encode information that can hardly be exploited by conventional classification algorithms. Machine learning (ML) techniques give their best in these types of classification problems. In this paper, we evaluate their performance against conventional (deterministic) algorithms. We demonstrate that both Convolutional Neural Networks (CNN) and Transformer-Encoder methods outperform deterministic algorithms in one of the most challenging classification problems of low-energy physics (single- versus double-beta events). We discuss the advantages and pitfalls of Transformer-Encoder methods versus CNN and employ these methods to optimize the detector parameters, with an emphasis on the DUNE Phase II detectors ("Module of Opportunity").

Trainability barriers and opportunities in quantum generative modeling

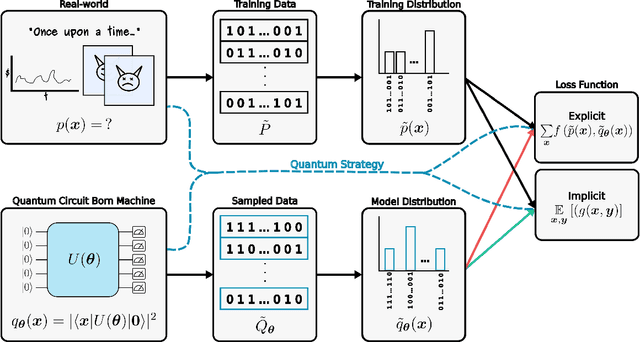
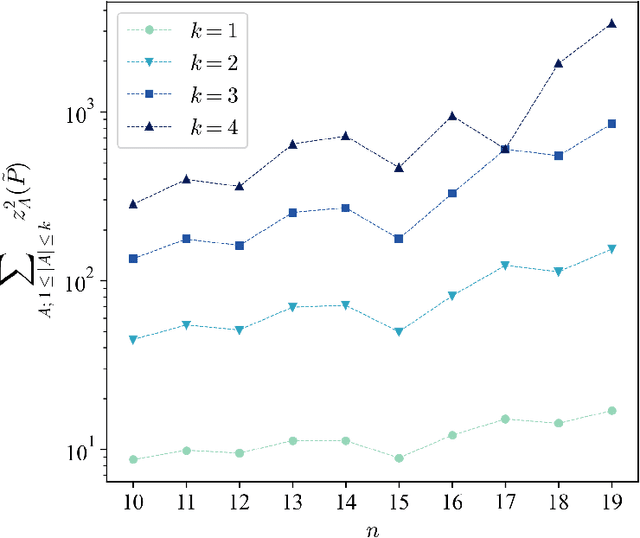
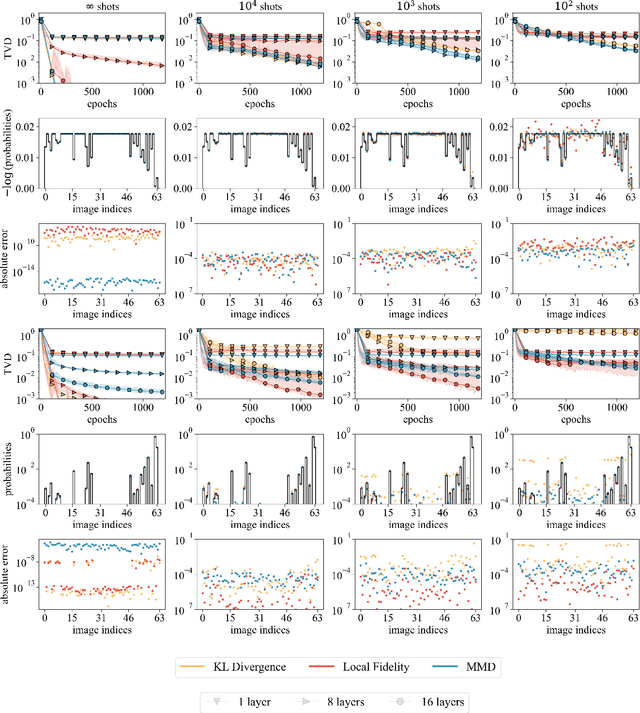
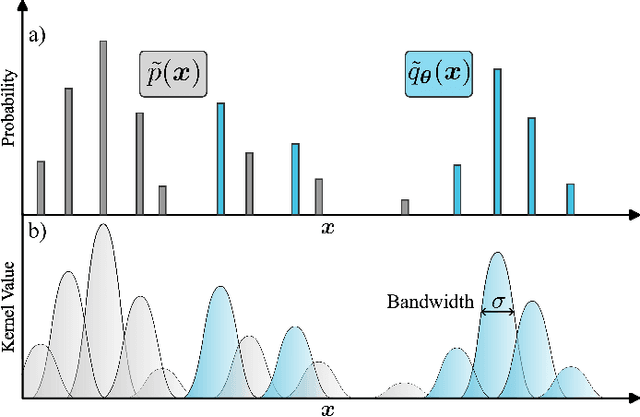
Quantum generative models, in providing inherently efficient sampling strategies, show promise for achieving a near-term advantage on quantum hardware. Nonetheless, important questions remain regarding their scalability. In this work, we investigate the barriers to the trainability of quantum generative models posed by barren plateaus and exponential loss concentration. We explore the interplay between explicit and implicit models and losses, and show that using implicit generative models (such as quantum circuit-based models) with explicit losses (such as the KL divergence) leads to a new flavour of barren plateau. In contrast, the Maximum Mean Discrepancy (MMD), which is a popular example of an implicit loss, can be viewed as the expectation value of an observable that is either low-bodied and trainable, or global and untrainable depending on the choice of kernel. However, in parallel, we highlight that the low-bodied losses required for trainability cannot in general distinguish high-order correlations, leading to a fundamental tension between exponential concentration and the emergence of spurious minima. We further propose a new local quantum fidelity-type loss which, by leveraging quantum circuits to estimate the quality of the encoded distribution, is both faithful and enjoys trainability guarantees. Finally, we compare the performance of different loss functions for modelling real-world data from the High-Energy-Physics domain and confirm the trends predicted by our theoretical results.

Unravelling physics beyond the standard model with classical and quantum anomaly detection

Much hope for finding new physics phenomena at microscopic scale relies on the observations obtained from High Energy Physics experiments, like the ones performed at the Large Hadron Collider (LHC). However, current experiments do not indicate clear signs of new physics that could guide the development of additional Beyond Standard Model (BSM) theories. Identifying signatures of new physics out of the enormous amount of data produced at the LHC falls into the class of anomaly detection and constitutes one of the greatest computational challenges. In this article, we propose a novel strategy to perform anomaly detection in a supervised learning setting, based on the artificial creation of anomalies through a random process. For the resulting supervised learning problem, we successfully apply classical and quantum Support Vector Classifiers (CSVC and QSVC respectively) to identify the artificial anomalies among the SM events. Even more promising, we find that employing an SVC trained to identify the artificial anomalies, it is possible to identify realistic BSM events with high accuracy. In parallel, we also explore the potential of quantum algorithms for improving the classification accuracy and provide plausible conditions for the best exploitation of this novel computational paradigm.

Quantum anomaly detection in the latent space of proton collision events at the LHC

We propose a new strategy for anomaly detection at the LHC based on unsupervised quantum machine learning algorithms. To accommodate the constraints on the problem size dictated by the limitations of current quantum hardware we develop a classical convolutional autoencoder. The designed quantum anomaly detection models, namely an unsupervised kernel machine and two clustering algorithms, are trained to find new-physics events in the latent representation of LHC data produced by the autoencoder. The performance of the quantum algorithms is benchmarked against classical counterparts on different new-physics scenarios and its dependence on the dimensionality of the latent space and the size of the training dataset is studied. For kernel-based anomaly detection, we identify a regime where the quantum model significantly outperforms its classical counterpart. An instance of the kernel machine is implemented on a quantum computer to verify its suitability for available hardware. We demonstrate that the observed consistent performance advantage is related to the inherent quantum properties of the circuit used.

The Quantum Path Kernel: a Generalized Quantum Neural Tangent Kernel for Deep Quantum Machine Learning

Building a quantum analog of classical deep neural networks represents a fundamental challenge in quantum computing. A key issue is how to address the inherent non-linearity of classical deep learning, a problem in the quantum domain due to the fact that the composition of an arbitrary number of quantum gates, consisting of a series of sequential unitary transformations, is intrinsically linear. This problem has been variously approached in the literature, principally via the introduction of measurements between layers of unitary transformations. In this paper, we introduce the Quantum Path Kernel, a formulation of quantum machine learning capable of replicating those aspects of deep machine learning typically associated with superior generalization performance in the classical domain, specifically, hierarchical feature learning. Our approach generalizes the notion of Quantum Neural Tangent Kernel, which has been used to study the dynamics of classical and quantum machine learning models. The Quantum Path Kernel exploits the parameter trajectory, i.e. the curve delineated by model parameters as they evolve during training, enabling the representation of differential layer-wise convergence behaviors, or the formation of hierarchical parametric dependencies, in terms of their manifestation in the gradient space of the predictor function. We evaluate our approach with respect to variants of the classification of Gaussian XOR mixtures - an artificial but emblematic problem that intrinsically requires multilevel learning in order to achieve optimal class separation.

Mixed Quantum-Classical Method For Fraud Detection with Quantum Feature Selection

This paper presents a first end-to-end application of a Quantum Support Vector Machine (QSVM) algorithm for a classification problem in the financial payment industry using the IBM Safer Payments and IBM Quantum Computers via the Qiskit software stack. Based on real card payment data, a thorough comparison is performed to assess the complementary impact brought in by the current state-of-the-art Quantum Machine Learning algorithms with respect to the Classical Approach. A new method to search for best features is explored using the Quantum Support Vector Machine's feature map characteristics. The results are compared using fraud specific key performance indicators: Accuracy, Recall, and False Positive Rate, extracted from analyses based on human expertise (rule decisions), classical machine learning algorithms (Random Forest, XGBoost) and quantum based machine learning algorithms using QSVM. In addition, a hybrid classical-quantum approach is explored by using an ensemble model that combines classical and quantum algorithms to better improve the fraud prevention decision. We found, as expected, that the results highly depend on feature selections and algorithms that are used to select them. The QSVM provides a complementary exploration of the feature space which led to an improved accuracy of the mixed quantum-classical method for fraud detection, on a drastically reduced data set to fit current state of Quantum Hardware.